【二叉树】已知 前中、前后、中后 遍历,怎么逆推回二叉树原貌?
前序、中序、后序都是啥
指的是遍历二叉树的顺序
- 前序遍历(preorder) : 根 左 右
- 中序遍历(inorder) : 左 根 右
- 后序遍历(postorder) : 左 右 根
对应leetcode:
思考
- 为什么给定一种遍历,不能逆推呢?
-->只给前序遍历对应的数组 vector, 那只知道vector[0]是根节点,vector.back()是右子节点,中间从哪开始是左节点?不知道
-->只给中序遍历对应的数组 vector,只知道左、右
-->只给后序遍历对应的数组 vector,只知道左、根 - 为什么给任两个就可以了呢?
-->前+中,preorder[0]是根节点,可以找到中序里的对应索引index, 那左边就是左节点,右边是右节点
核心思想:
- 找根节点位置,一个二叉树肯定先要有一个根节点不是
-->前+中,preorder[0]是根节点 - 找到根节点后,根节点左边的肯定属于左叶子节点,右边的属于右叶子节点,从而确定出 左 右 搜索的范围
-->inorder[index]对应的值就是preorder[0], 则inorder里的左叶子范围[in_start, index-1], 右叶子范围[index+1, in_end]
已知前序(preorder)、中序(inorder),逆推二叉树
按照上面核心思想:
根节点 pretorder[pre_start] = inorder[index], 怎么找到index呢?最简单的就是 for(auto& i : inorder) 来找到对应的index,但这样每次都要循环,浪费,可以放到 哈希表里 快速访问。
在中序遍历里 左叶子范围[in_start, index-1], 右叶子范围[index+1, in_end]
class Solution {
public:
unordered_map<int,int> hash;
int pre_index;
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
for(int i=0; i<inorder.size(); ++i){
hash[inorder[i]] = i;
}
pre_index = 0;
return dfs(preorder, 0, inorder.size()-1);
}
TreeNode* dfs(vector<int>& preorder, int in_left, int in_right){
if(in_left>in_right) return nullptr;
int root_val = preorder[pre_index];
TreeNode* root = new TreeNode(root_val);
int index = hash[root_val];
pre_index++;
root->left = dfs(preorder, in_left, index-1);
root->right = dfs(preorder, index+1, in_right);
return root;
}
};
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
// 中 左 右
// 左 中 右
int n = preorder.size();
TreeNode* root = new TreeNode(preorder[0]);
stack<TreeNode*> s;
s.push(root);
int inIndex = 0;
for (int i = 1; i < n; ++i) {
// 当前节点
auto cur = new TreeNode(preorder[i]);
// 上一个节点
auto pre = s.top();
// 如果pre不在inorder中,则cur是pre的左子节点,否则为pre的父节点的右子节点
if (pre->val != inorder[inIndex]) {
pre->left = cur;
}
else {
while (!s.empty() && s.top()->val == inorder[inIndex]) {
pre = s.top();
s.pop();
inIndex++;
}
pre->right = cur;
}
s.push(cur);
}
return root;
}
};

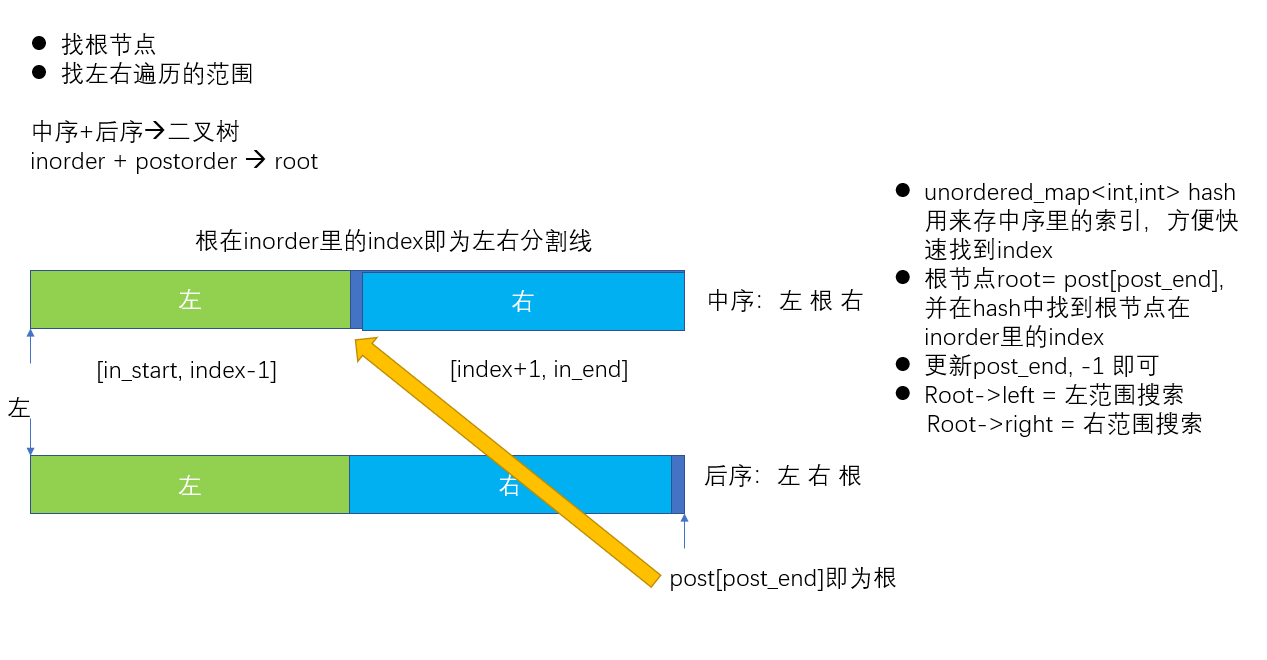
已知中序(inorder)、后序(postorder), 逆推二叉树
按照上面核心思想:
根节点 postorder[post_end] = inorder[index], 怎么找到index呢?最简单的就是 for(auto& i : inorder) 来找到对应的index,但这样每次都要循环,浪费,可以放到 哈希表里 快速访问。
在中序遍历里 左叶子范围[in_start, index-1], 右叶子范围[index+1, in_end]
class Solution {
public:
unordered_map<int,int> hash;
int post_index;
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
post_index = postorder.size()-1;
for(int i=0; i<inorder.size(); ++i){
hash[inorder[i]] = i;
}
return dfs(postorder, 0, inorder.size()-1);
}
TreeNode* dfs(vector<int>& postorder, int in_left, int in_right){
// 如果这里没有节点构造二叉树了,就结束
if (in_left > in_right) return nullptr;
int root_val = postorder[post_index];
TreeNode* root = new TreeNode(root_val);
int index = hash[root_val];
post_index--;
root->right = dfs(postorder, index+1, in_right);
root->left = dfs(postorder, in_left, index-1);
return root;
}
};
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
// 左 根 右
// 左 右 根
int n = inorder.size();
TreeNode* root = new TreeNode(postorder[n - 1]);
stack<TreeNode*> s;
s.push(root);
int inIndex = n - 1;
for (int i = n - 2; i >= 0; --i) {
TreeNode* cur = new TreeNode(postorder[i]);
TreeNode* pre = s.top();
// pre 不在 inorder 右侧,则不是右节点,是根节点
if (pre->val != inorder[inIndex]) {
pre->right = cur;
}
// 否认cur是pre父节点的左节点
else {
while (!s.empty() && s.top()->val == inorder[inIndex]) {
pre = s.top();
s.pop();
inIndex--;
}
pre->left = cur;
}
s.push(cur);
}
return root;
}
};
已知前序(preorder)、后序(postorder), 逆推二叉树
这里有些不同,根节点很明显 preorder[pre_start] = postorder[post_end], 没法区分呀,那其实应该转换思路,找出左右节点的区分了
preorder里的第一个左节点一定是postorder里的最后一个左节点,因此把上面思路中的根节点换成左节点,找出左节点在postorder中的index,就能锁定范围了
class Solution {
public:
unordered_map<int,int> hash;
TreeNode* constructFromPrePost(vector<int>& pre, vector<int>& post) {
int n = pre.size();
for(int i=0; i<n; ++i){
hash[post[i]] = i;
}
return dfs(pre, post, 0, n-1, 0, n-1);
}
TreeNode* dfs(vector<int>& pre, vector<int>& post,
int pre_left, int pre_right,
int post_left, int post_right){
if(pre_left>pre_right || post_left>post_right) return nullptr;
TreeNode* root = new TreeNode(pre[pre_left]);
if(pre_left==pre_right) return root;
int index = hash[pre[pre_left+1]];//左节点在post里的位置
int leftLen = index-post_left+1;//左节点长度
root->left = dfs(pre, post, pre_left+1, pre_left+leftLen, post_left, index);
root->right = dfs(pre, post, pre_left+leftLen+1, pre_right, index+1, post_right-1);
return root;
}
};



