Mathematical-Analysis-I-3
\(\S\) 3.1 函数的极限
重要极限(书上)
常用极限
-
\(\mathop{\lim}\limits_{x \to \infty}\Large \frac{x^k}{a^x} \normalsize= 0\) (通过 \(\mathop{\lim}\limits_{n \to \infty}\Large \frac{n^k}{a^n} \normalsize= 0, n\in \mathbb{N}\) 证明)
-
所有等价无穷小量
-
\(\mathop{\lim}\limits_{x \to \infty} \large \frac{1}{x} \normalsize = 0\)
-
\(\mathop{\lim}\limits_{x \to 1} \Large \frac{\sqrt{x} - 1}{x - 1} \normalsize = \Large \frac{1}{2d}\)
-
\(\mathop{\lim}\limits_{x \to \Box}u(x)^{v(x)} = a ^ b\)
3.2 连续函数
连续函数可移动极限位置:\(\mathop{\lim}\limits_{x \to \Box}f(g(x)) = f(\mathop{\lim}\limits_{x \to \Box}g(x))\)
定理3.3.1:有界性
设 \(f(x)\in C[a,b]\) 则 \(f(x)\) 在 \([a,b]\) 上有界。也就是像下图说的那样
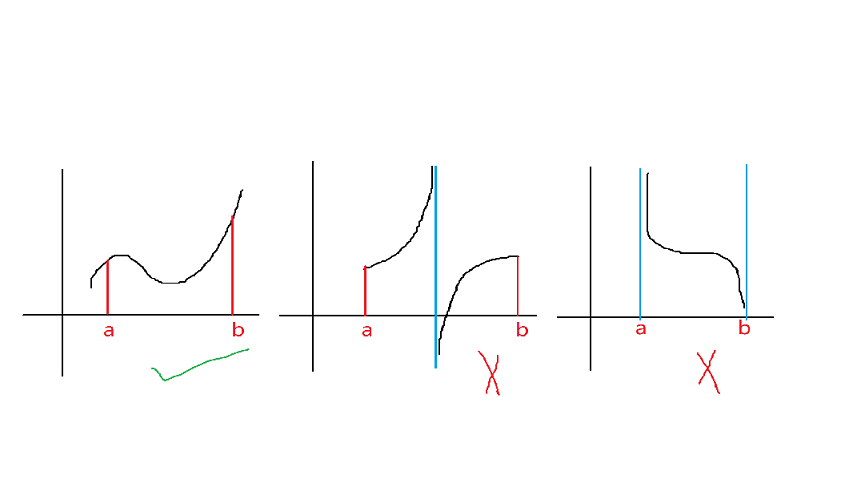
无穷大 \(\subset\) 无界
定理3.3.2:最值定理
设 \(f(x) \in C[a,b]\) ,则 \(f(x)\) 在 \([a,b]\) 上必有最小值和最大值。
很好理解,同上图。
定理3.3.3:介值定理
设 \(f(x) \in C[a,b]\) ,设 \(m=\mathop{min}\limits_{x \in [a,b]} \{ f(x) \}\) ,\(M=\mathop{max}\limits_{x\in [a,b]}\{f(x)\}\) ,则对,\(\forall \,\eta \in [m,M]\) ,\(\exists \,\xi \in [a,b]\) 使得 \(f(\xi)=\eta\) ,也即 \(f([a,b]) = [m,M]\)
人话:若 \(f(x)\) 在 \([a,b]\) 连续,则在最大最小值之间的任何一个数都至少对应一个 \(x\)
一致连续
理解
一致连续不仅要连续,还要当距离足够近时,函数值没有明显的变化。
反应到图像上,连续就是一笔画曲线,而一致连续不仅要一笔画,还要求特定的区域内图像不能过于陡峭(比如1/x, 在0附近时)。
定理
\(\textrm{cantor}\) 定理
一致连续等价于:变成序列的 \(x_1,x_2\) 之差趋于 \(0\) ,则对应的变成序列的 \(f(x_1), f(x_2)\) 之差也趋于 \(0\)
证明在 \([0,+\infty)\) 上连续的时候,需要取 \(\mathop{[1,+\infty)}\limits_{\textbf{用定义证明}},\mathop{[0,2]}\limits_{\textbf{用cantor}}\) 两个区间,一定要相交!!!保证 \(x_1,x_2\) 落在同一区间
\(\S\) 3.4 无穷小量与无穷大量的阶
-
无穷大量和无穷小量都需要说明 在 \(x\to \Box\) 时
-
\(o(g(x))\)
-
通过 \(\mathop{\lim}\limits_{x \to \infty}\Large \frac{x^k}{a^x} \normalsize= 0\) 可证明 \(x^k=o(a^x)\) , \(\log_ax = o(x^k)\) ,有一种记法: \(\log_a x \prec x^k \prec a^x\)
-
\(f(x) \sim g(x) \Longleftrightarrow f(x) = g(x) = o(g(x))\)
求无穷小量的方法
-
通过等价无穷小量化简
-
如果给了无穷小量的格式并且原式无法化简,那么想办法提出这个格式,使得剩下的部分趋于 \(1\) 。
例:求 \(\sqrt{x + \sqrt{x + \sqrt{x}}}\;(x \to 0)\) 的形如 \(ax^{\alpha}\) 的等价无穷小量。
这题只能用第二种方法。
想办法提出一个 \(ax^{\alpha}\) 让剩下的部分等于 \(1\) 。显然 \(a=1\) (这个式子不提常数常数是最方便的)。技巧: 考虑到 \(x \to 0\) 时 \(x^{\large\frac{p}{q}}\to 0\; (\frac{p}{q}>0)\) ,故只需要里面次数最小的变为 \(1\) 即可,也就是把最里面的 \(\sqrt{x}\) 变成 \(1\) 。得到
这样就可以得到右边的部分趋于 \(1\; (x \to 0)\) ,我们就求得了等价无穷小量。
同理: \(\sqrt{x + \sqrt{x + \sqrt{x}}}\;(x \to +\infty)\) 的形如 \(ax^{\alpha}\) 的等价无穷大量,也可通过以下式子得到
相关证明
定理3.3.1:有界性
证明1:
方法很多,这里的第一种方法使用 \(Bolzano-Weierstrass\) 定理和 \(Henie\) 定理
证1:(反证法)
假设 \(f(x)\) 在 \([a,b]\) 上连续,但是无界. 则根据无界的定义\[\forall \, M>0, \exists\,x_0 \in [a,b], \textrm{使得}\; |f(x)|>M \]无界可以联想到无穷大,但必须取离散的点作为自变量才能保证无穷大。由无穷大可以找矛盾点:在这些离散点的定义下存在极限等于实数。可以考虑 \(Bolzano\) ,然后因为在函数下讨论序列问题,可以考虑用 \(Henie\) 。
则取 \(M\) 等于 \(1,2,\cdots,n\) ,有
\[1>0,\exists\,x_1\in[a,b], |f(x)|>1\\ 2>0,\exists\,x_2\in[a,b], |f(x)|>2\\ \vdots\\ n>0,\exists\,x_n\in[a,b], |f(x)|>n\\ \]从而有 \(\mathop{lim}\limits_{n \to \infty}f(x_n)=\infty\)
现在我们得到了一个数列 \(\{x_n\}\) ,它不一定收敛,但它有界,则有 \(Bolzano\) 定理可得它一定有收敛子列,不妨记作 \(\{x_{n_k}\}\) ,收敛于 \(x_0\)
加之 \(f(x)\) 在 \([a,b]\) 上连续(闭区间,则极限一定能够等于当前点的函数值),结合 \(Henie\) 定理,\(\mathop{lim}\limits_{k\to \infty}x_{n_k}=x_0 \Longrightarrow\mathop{lim}\limits_{k\to\infty}f(x_{n_k})=f(x_0)\)
如果一个数列收敛于一个数或者无穷,那么它的子列也收敛到同一个数或无穷。此处就产生了矛盾。
证毕
证明2
闭区间套
证2:(反证法)
假设 \(f(x)\) 在 \([a,b]\) 上连续,但是无界,则对于区间 \([a,\frac{a+b}{2}]\) 和 \([\frac{a+b}{2},b]\) ,\(f(x)\) 一定在其中的某个区间内无界。令这个子区间为 \([a_1,b_1]\) 则对于 \([a_1,\frac{a_1+b_1}{2}]\) 和 \([\frac{a_1+b_1}{2},b_1]\) ,\(f(x)\) 一定在其中的某个区间内无界。
如此下去,则可以得到一个闭区间列 \(\{[a_n,b_n]\}\) 满足:
\(1. a_{n-1}\le a_n<b_n\le b_{n-1}\)\(2. \mathop{lim}\limits_{n\to\infty}b_n-a_n=0\)
\(3. f(x)\) 在每个区间上无界
则由闭区间套定理,\(\exists!\,c\in[a_n,b_n],\forall n\in\mathbb{N}\) .
由条件 \(2\) 知 \(\exists n>0\) 使得 \([a_n,b_n] \subset U(c,\delta)\) 即 \(f(x)\) 无界。由连续函数的局部有界性,\(\exists\, \delta>0\) ,使得当 \(\forall x\in U(c,\delta)\) 时,\(f(x)\) 有界。
这与条件 \(3\) 矛盾
证毕
3.3.2 最值定理
证明:
由连续函数的有界性定理,\(f(x)\) 一定有界。
记 \(M=\mathop{sup}\limits_{x\in[a,b]}\{f(x)\}\) , \(m=\mathop{inf}\limits_{x\in[a,b]} \{ f(x) \}\)
由上确界的定义,可得上确界是 \(f(x)\) 的一个聚点。则存在数列 \(\{ x_n \}\) 使得 \(\mathop{lim}\limits_{n\to\infty} f(x_n) = M\) 。
下面证明存在一个数 \(\xi\) 使得 \(f(\xi) = M\) :设 \(\{ x_{n_k} \}\) 是 \(\{ x_n \}\) 的子列,因为 \(\{ x_{n_k} \}\) 有界,则 \(\{ x_{n_k} \}\) 必收敛,设收敛于 \(x_0\) 。
由 \(Henie\) 定理: \(\mathop{lim}\limits_{k \to \infty} f(x_{n_k}) = M\)
因为 \(f(x)\) 连续,所以有 \(\mathop{lim}\limits_{k \to \infty} f(x_{n_k}) = f(x_0)\)
故有 \(f(x_0) = M\) 即可以取到最大值。
同理可证最小值
证毕。
定理3.3.3:介值定理
证明:
证: \(m = M\) 时,显然成立。
\(m \ne M\) 时,\(\exists \, x_1,x_2 \in [a,b], \, f(x_1) = m, \, f(x_2) = M\) 。显然当 \(\eta = m\) 或 \(M\) 时成立。
假设 \(x_1 < x_2\),当 \(\eta \in (m,M)\) 时,定义:\(E = \{ x \in [x_1,x_2]: f(x) > \eta \}\)
显然 \(x_1 \notin E\) ,故 \(x_1\) 是 \(E\) 的下界
显然 \(x_2 \in E\) ,故 \(E\) 非空
因此 \(E\) 一定存在下界。
记 \(\xi = inf\,E\) ,则有 \(x_1 \le \xi <x_2\)
由连续函数的局部保号性知:\(\exists \, \delta > 0, \forall \, x \in (x_1,x_1 + \delta) ,f(x) <= \eta\)
设 \(x_* \in (x_1,x_1 + \delta)\) 因为 \(\xi\) 是下界,故有 \(\xi \ge x_* > x_1\) 因此 \(\xi\) 严格大于 \(x_1\)下证 \(f(\xi) = \eta\) :
由 \(E\) 的定义,\(f(\xi) \ge \eta\) 。
若 \(f(\xi) > \eta\) 则由 \(f(x)\) 在 \(\xi\) 处连续可得:\(\exists \, \delta > 0, \forall \, x \in (\xi - \delta,\xi + \delta) \cap [a,b],f(x) > \eta\)
但因为 \(\xi\) 为下界,故对于 \(x \in (\xi - \delta,\xi),f(x) \le \eta\) ,矛盾
证毕


