Mathematical-Analysis-I-2

序列极限的定义

收敛与发散

\(N\) 依赖于 \(\varepsilon\) ，求 \(N\) 就是解不等式

几何语言：任意 \(\varepsilon\) 领域外面只有有限项

以下概念在定义时有区别：

发散	收敛的逆命题（对任意 \(A\) ）	\(\forall A \in \mathbb{R},\exists \varepsilon_0 > 0,s.t.\forall N \in \mathbb{N},\exists n_N > N, \vert x_{n_N} - A\vert \ge \varepsilon_0\)
不收敛于 \(A\)	收敛于 \(A\) 的逆命题（对给定的 \(A\) ）	\(\exists \varepsilon_0 > 0 s.t. \forall N \in \mathbb{N}, \exists n_N > N, \vert x_{n_N} - A \vert \ge \varepsilon_0\)
无穷大量	发散的一种特殊情况（单调地趋于无穷）	\(\forall M > 0,\exists N \in \mathbb{N}, s.t.\forall n > N,\vert x \vert \ge M\)
无界	单调或者不单调地趋于无穷（包含无穷大、振荡、分段函数等多种情况）

求序列极限（极限存在才能求）

要么证明极限存在，要么用上下极限相等。

两边求极限之后 \(<\) 可写作 \(\le\)

求序列极限的时候，看看 \(n\to \infty\) 时，序列趋大还是趋小，趋大就要在分母上做文章，不好判断的另说

特殊的极限:

\[\lim_{n \to \infty}\sqrt[n]{n} = 0 \\ \lim_{n \to \infty}\sqrt[n]{a} = 1(a > 1) \]

常用的方法：

1. 取对数
2. 令 \(q(q>1) = 1 + h_n\) ，再利用二项式展开。
3. 加一项，减一项使得与已知极限发生关系
4. 有理分式求极限的时候，如果上下次数相同，可以提出最高项
5. 等价无穷小替换（只能乘除）
6. 无法用等价无穷小替换的时候，通过别的方法配凑出重要极限 \(\mathop{\lim}\limits_{x \to 0} \Large \frac{\sin x}{x} \normalsize = 1\)，\(\mathop{\lim}\limits_{x \to 0} (1 + x)^{\frac{1}{x}} \normalsize = e\)
7. 上下极限相等（上下极限可以直接取而不用证明极限存在）
8. 夹逼定理 \(+\) 不等式
9. 对于函数极限，想办法找到 \(\vert x - x_0 \vert\) 的结构，再把其他的部分放缩掉

需要养成的观点：解不等式时是有大量放缩的，不仅有对式子的放缩，还有对 \(n,N\) 的放缩，以及对 \(\varepsilon, M\) 等等右边的东西的放缩

无穷小量无穷大量

有界变量 \(\times\) 无穷小量 = 无穷小量

重点：例 \(2.1.13\) 见书

序列极限的性质

1. 改变有限项不改变收敛情况
2. 收敛序列有界
3. 保序性：在 \(n\) 足够大时：数列大小可推极限大小（加等号）。（其中包括常数列）。在不等于极限值的情况下极限大小可推数列大小
4. 夹逼定理

重要定理

两个常数

\[\begin{align} &e\\ \sum_1^n\frac{1}{k} =& c + \ln n + o(1) \end{align} \]

定理

单调收敛：上升有 \(\mathop{\lim}\limits_{n \to \infty} = \sup\{x_n\}\)，下降有 \(\mathop{\lim}\limits_{n \to \infty} = \inf\{x_n\}\)

闭区间套（常常与二分搭配证明，有限步与无限步为两种不同的情况）：闭区间，包含与无限短三个限定条件，唯一的一个 \(c\)

有限覆盖定理（连接局部与整体的桥梁）：开区间去覆盖闭区间,本质是缩减规模

聚点原理（对象为集合）：

1. \(x_0\) 为 \(E\) 聚点
2. 存在不相同的点构成趋近于 \(x_0\) 的子序列
3. \(x_0\) 的任意去心领域都与 \(E\) 有交集（在 \(x_0\) 处有无限多项）

列紧性定理 \(\textrm{Bolzano-Weierstrass}\) ：

柯西收敛准则（判断极限存在）

*压缩映照原理

\(\textrm{Stolz}\)定理

上下极限（序列）

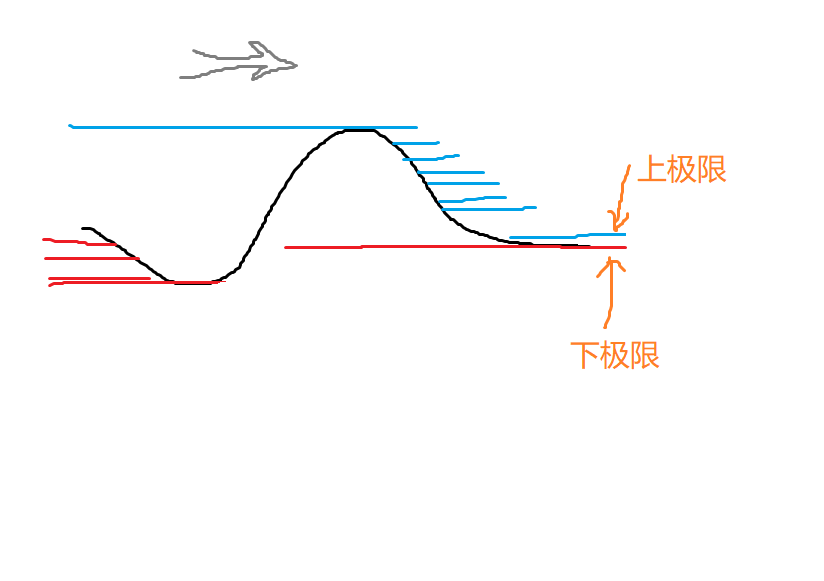
\(\mathop{\underline{\lim}}\limits_{n \to \infty} x_n \le \mathop{\overline{\lim}}\limits_{n \to \infty} x_n\)

等价命题：

1. \(h\) 为上极限
2. 所有收敛的子列的 \(\lim \le h\)
3. \(h\) 既是 \(x\) 的极限，又是 \(n\to \infty\) 时一部分 \(x\) 的上界

定理

1. 若序列 \(\{ x_n\}\) 有界且两两不同，则上极限为最大聚点，下极限为最小聚点
2. 子列的上下极限被序列的上下极限包着
3. 极限存在等价于上下极限相等（同时也等于极限）

性质

大部分与正常极限相同

两个不等式：两个下相加 \(\le\) 和的下极限 \(\le\) 一上一下 \(\le\) 和的上极限 \(\le\) 两个上相加（加、乘相同）

\[\mathop{\underline{\lim}}\limits_{n \to \infty} x_n + \mathop{\underline{\lim}}\limits_{n \to \infty} y_n \le \mathop{\underline{\lim}}\limits_{n \to \infty}(x_n + y_n) \\ \le \mathop{\underline{\lim}}\limits_{n \to \infty} x_n + \mathop{\overline{\lim}}\limits_{n \to \infty} y_n \\ \le \mathop{\overline{\lim}}\limits_{n \to \infty}(x_n + y_n) \\ \le \mathop{\overline{\lim}}\limits_{n \to \infty}x_n + \mathop{\overline{\lim}}\limits_{n \to \infty} y_n \tag{1} \]

\[\mathop{\underline{\lim}}\limits_{n \to \infty} x_n \cdot \mathop{\underline{\lim}}\limits_{n \to \infty} y_n \le \mathop{\underline{\lim}}\limits_{n \to \infty}(x_n \cdot y_n) \\ \le \mathop{\underline{\lim}}\limits_{n \to \infty} x_n \cdot \mathop{\overline{\lim}}\limits_{n \to \infty} y_n \\ \le \mathop{\overline{\lim}}\limits_{n \to \infty}(x_n \cdot y_n) \\ \le \mathop{\overline{\lim}}\limits_{n \to \infty}x_n \cdot \mathop{\overline{\lim}}\limits_{n \to \infty} y_n \tag{2} \]

一个等式：

\[\mathop{\overline{\lim}}\limits_{n \to \infty} \frac{1}{x_n} = \frac{1}{\mathop{\underline{\lim}}\limits_{n \to \infty} x} \tag{3} \]

相关定义