《T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction》 论文解读
论文链接:https://arxiv.org/abs/1811.05320
最近发现博客好像会被CSDN和一些奇怪的野鸡网站爬下来?看见有人跟爬虫机器人单方面讨论问题我也蛮无奈的。总之原作者Missouter,博客链接https://www.cnblogs.com/missouter/,欢迎交流。
整理、精炼了一下这篇论文的思路。
Abstract:
交通预测的难点在于交通拓扑网络复杂的结构与随时间动态发生的交通变化;为了提取交通网的空间与时间特征,文章提出了一种时间性的图卷积网络模型,结合了门级循环单元(GRU)与图卷积网络(GCN)。其中图卷积网络被用于提取复杂拓扑结构中的空间性信息,而门级循环单元则为了提取时间关系,被用于学习交通数据中的动态数据。
Introduction:
交通预测过程:分析交通道路状况,包含流量、速度、密度;挖掘交通模式,同时对道路上的交通状况进行预测。
预测结果:交通管理者预测拥堵状况、限制交通工具的科学基础、出行者效率选择出行工具、路线的保障。
难点:
1、 空间关系:交通流的变化被拓扑结构的城市交通网主导,上游的交通状态通过传输作用影响下游的交通状态,而下游交通状态通过反馈作用再影响上游交通。
2、 时间关系:交通流随时间动态变化,主要表现在周期性和趋势上;现有的交通状况被前一刻的交通状况影响。
现存交通预测方法缺陷:一些交通预测方法(ARIMA、Kalman filtering model,etc)只关注了交通状况的动态变化而忽视了空间关系,导致交通状态的变化不被道路网约束,同时一些模型尝试使用卷积神经网络进行空间性建模,但这些模型一般只使用于欧几里得类型的数据(规则矩阵、图像等),无法在拓扑结构的城市交通网络中运作。
T-GCN贡献:
1、 结合了GCN与GRU,内容与abstract重复,不做多提。
2、 T-GCN的预测结果展示了一个不同视角下的稳定状态,表示T-GCN除了预测短周期的变化,还能预测长周期的变化。
3、 我们使用两个现实的数据集评估模型,相较其他预测模型,减少了1.5%~57.8%的预测错误率。
Related work:
交通预测方法分类:模型驱动的方法、数据驱动的方法;
模型驱动的方法:解释即时、稳定的交通关系如交通流量、速度与密度,需要复杂细致的系统建模与巨大的算力,且由于诸多因素的影响,现实环境中交通数据的多样性无法被精确描绘。
数据驱动的方法:基于数据统计所得规律推断交通状况的变化。不分析物理属性与交通系统的动态变化有着较高的复杂度。其中的historical average model不需要假设、计算过程简单,但精确度不佳。
拥有更高精确度的模型被提出,分为两种:含参数的与非参数的。
含参模型假定回归函数,参数在对原始数据的处理过程中确定。传统含参的模型是在系统模型为静态的假设基础上建立的,反映不了交通系统的非线性与不确定性,也克服不了交通事故等突发随机事件的困难。不含参数的模型只需要足够的历史数据就能自动学习静态规律特征,但先前形如LSTM、GRU的模型仅仅考虑了时间关系而忽略了空间关系,不能精确预测道路上的交通信息,如何充分利用空间信息成了交通预测的关键,而利用CNN进行空间关系提取的模型虽然在交通预测上取得了显著进步,但无法应用于复杂拓扑结构的城市交通网,随着GCN研究的深入,拓扑结构空间特征的提取问题也得到解决。
(这段论文写的有点长…堆了一堆文字读的我有点难受)
Methodology:
问题定义:根据历史数据预测某一特定时间段的交通信息,交通数据通常被定义为速度、密集程度、交通流。使实验不失普遍性,在实验章节使用交通速度作为交通数据的代表。(Without loss of generality, we use traffic speed as an example of traffic information in experiment section.这句语感有点僵了)
定义:设定无权图G=(V, E),V、E分别代表道路点与边,N为道路的数量,设定邻接N*N矩阵A表达道路与道路之间的联系;设定N*P特征矩阵X,P代表点属性特征的数量,即历史时间序列的长度,使用N*i矩阵 表示在时刻i,每条道路上的速度,属性特征也可以是交通速度、交通流等属性。
问题转化:交通空间-时间性预测被转化为学习以拓扑图G为前置与特征矩阵X的映射函数,计算得到在下T时刻的交通信息:
![]()
过程概览:首先以长度为n的历史时间序列数据作为输入,使用GCN接收拓扑结构的空间信息,其次将接收到的空间、时间信息输入GRU当中,获取各个单元间的动态信息变化,以提取时间性的特征,最后在全连接层获得结果。
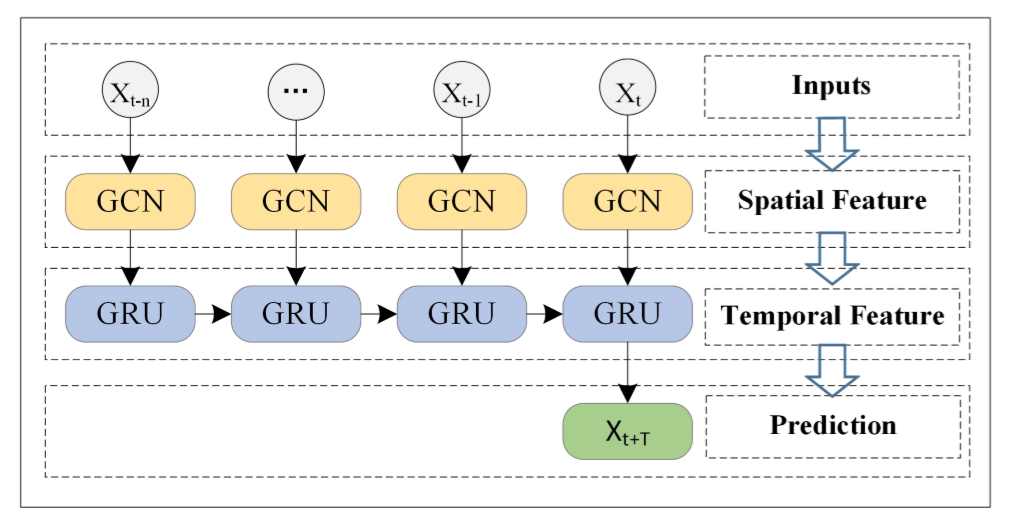
空间关系建模:利用GCN提取图结构的数据,通过给定的邻接矩阵A、特征矩阵X,GCN在图上通过提取相邻结点特征构建傅里叶域,使用堆叠的卷积网络,表示为:
![]()
Â为A与单位矩阵I相加所得, D为度矩阵, Hl为第l层的输出, θl包含该层的参数, σ代表非线性回归的激活函数。(我怀疑论文这里的上标打错了)
两层GCN模型可被表示为:
![]()
其中 ,P*H的 矩阵代表从输入到隐藏层的权重,P为特征矩阵的长度,H为隐藏单元的数量;H*T的W1代表从隐藏层到输出层的权重, f(X,A)∈RN*T代表长度为T的预测输出,ReLU()作为修正线性单元,作激活层用。
时间关系建模:被广泛应用的循环神经网络因梯度消失/爆炸的原因,不适用于长周期的预测;LSTM与GRU作为循环神经网络的变种,克服了上述问题。其共同原理都是利用门级机制储存尽可能长的周期信息;LSTM因其复杂的结构,GRU结构更加简单,故计算时间更短。
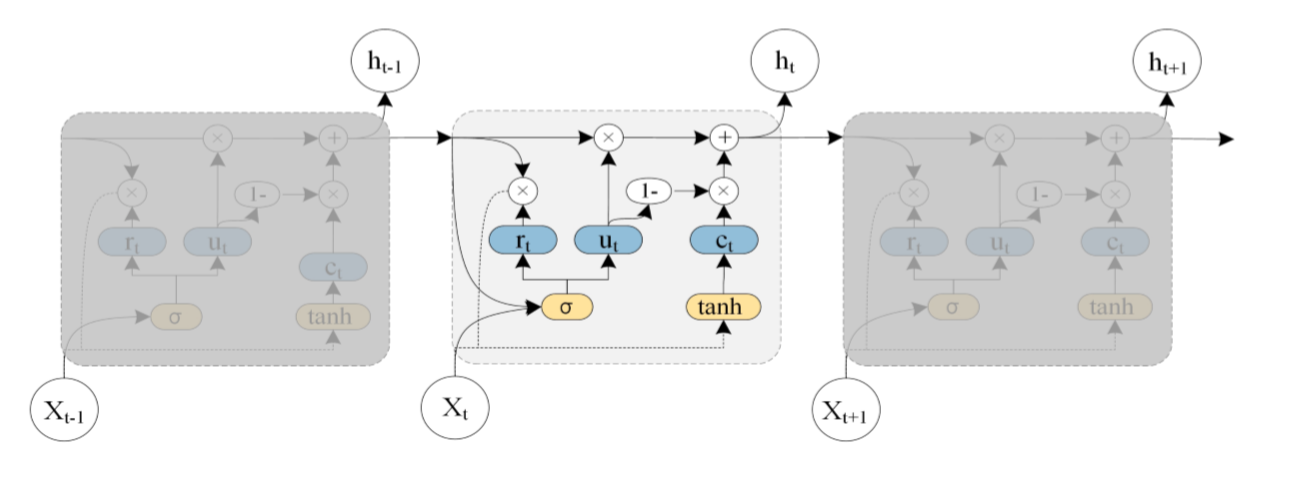
图中ht-1表示t-1时刻的隐藏状态, xt表示t时刻的交通信息, rt代表重置门,用于控制先前时刻状态信息的度量; ut为上传门,用于控制上传到下一状态的信息度量; ct为t时刻时储存的信息, ht为t时刻的输出状态;总的来说,GRU通过获取t-1时刻的隐藏状态与当时的交通状态信息得到t时刻的交通信息。
T-GCN:
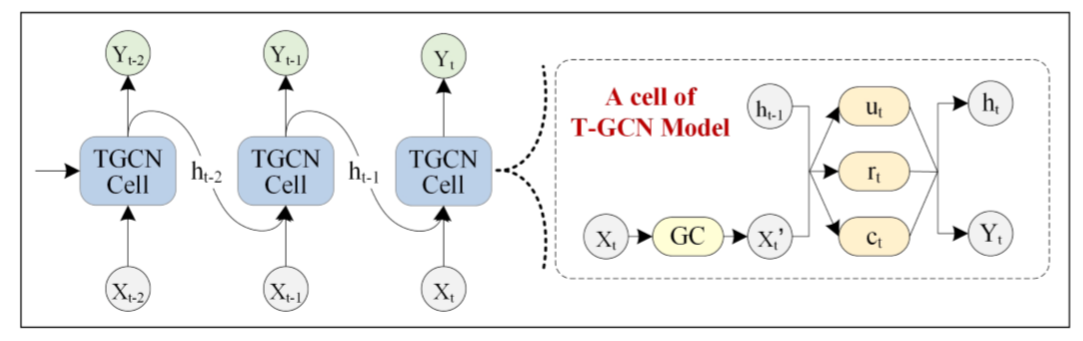
T-GCN的结构如图,右侧为T-GCN的处理单元: 为t-1时刻的输出,GC为图卷积过程,ut 、 rt分别为上传门与重置门, 为t时刻的输出。具体计算过程为:
![]()
![]()
![]()
![]()
f(A,X)代表前文定义的GCN计算过程,w与b代表训练过程中的权重与偏移量。(很大部分照搬了GNU的公式)
损失函数:
目标:最小化真实交通速度与预测交通速度的误差。Y分别代表真实速度与预测速度,损失函数如下:
![]()
其中 λLreg用于防止过拟合。
Experiments:
选取数据集:
1、SZ-taxi:数据分为两部分,156*156的邻接矩阵表示路与路之间的空间关系,描述每条路上随时间变化的特征矩阵。
2、Losloop:由邻接矩阵与特征矩阵组成,邻接矩阵由交通网络中的传感器计算;同时作者对数据集中的残缺部分使用线性填充的方法进行了补全。
输入的数据全部进行了归一化处理,80%的数据用于训练,而20%的数据被用于测试。实验对接下来15、30、45、60分钟的交通速度进行预测。
评价指标:
文章列出了五个用于评价T-GCN预测表现的指标:
1、均方根误差:
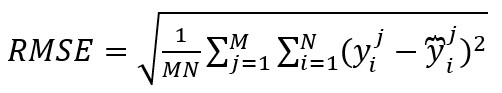
2、平均绝对误差:
![]()
3、准确率:
![]()
4、 确定系数:
![]()
5、可释方差值:
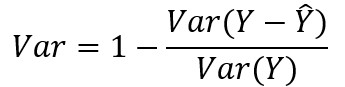
其中yj'i分别代表第j次时间、第i条路的真实交通信息与预测信息,M为时间样本的数量,N为路的数量,Y分别代表 与 的集合, 带上划线的Y为Y的平均数。
R2与var用于计算相关系数,衡量预测结果表示实际数据的能力,数值越大则预测能力越优越。
选取模型参数:
超参数:包括学习率(0.001)、抓取数量(32)、训练轮数(5000)、隐藏单元数量(通过多次实验取最优预测效果)
针对SZ-taxi文章选取[8,16,32,64,100,128],分析预测准确率的变化,得到不同隐藏单元数量下RASE与MAE、Accuracy、R2 、var的值如图:

显然数量为100时效果是最好的(真有这么巧的事情嘛…)。隐藏单元超过一定数量性能下降的原因在于数据单元超过一定值后计算复杂度增加,且训练数据会出现过拟合现象。
实验结果:
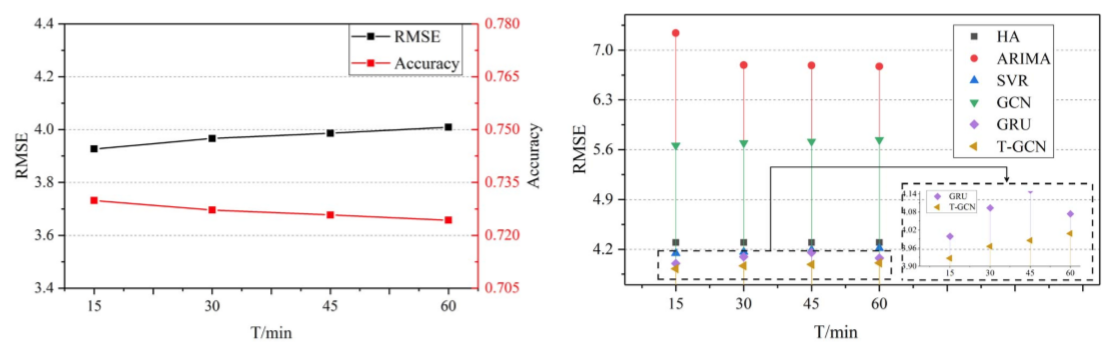
将T-GCN预测效果与baseline对比,包括HA、ARIMA、SVR、GCN、GRU,所得实验数据如下:

高预测精准度:门级循环网络的预测精度显著高于其他baseline算法,HA、ARIMA、SVR等算法因难以处理复杂、非固定的时间数据而预测效果不佳,GCN预测效果不佳的原因仅仅在于仅考虑了空间特征而忽略了交通数据是一个典型的时间序列数据这一事实。
ARIMA比HA检测效果弱的原因在于ARIMA不适用于长周期的检测,且计算每个节点误差的方式导致一些数据中的波动会导致最终的计算错误。
时空预测能力:为了检验模型是否能够从交通数据中提取时空特征,文章将模型与GCN、GNU模型进行了比较:
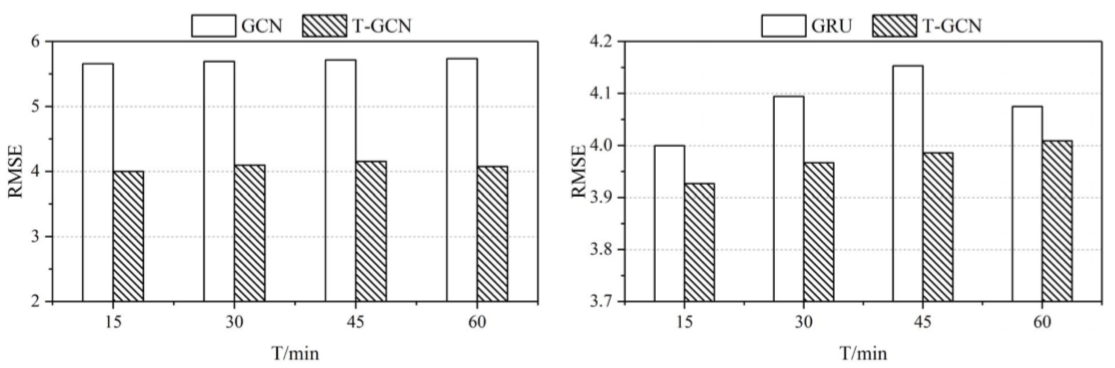
长周期预测能力:在不同的时间范围(文章只写了“horizon”,根据前后文认定为是时间范围)下,T-GCN都能获得最好的预测效果且预测结果拥有较小的变化趋势,证明了T-GCN拥有更好的长周期预测能力;文章以T-GCN在不同时间点的结果作为论证:
干扰分析与鲁棒性:通过向数据中添加两种不同的噪声检验T-GCN的鲁棒性,高斯分布、泊松分布的 值作为自变量被改变,分别添加到两种数据集上,得到结果:
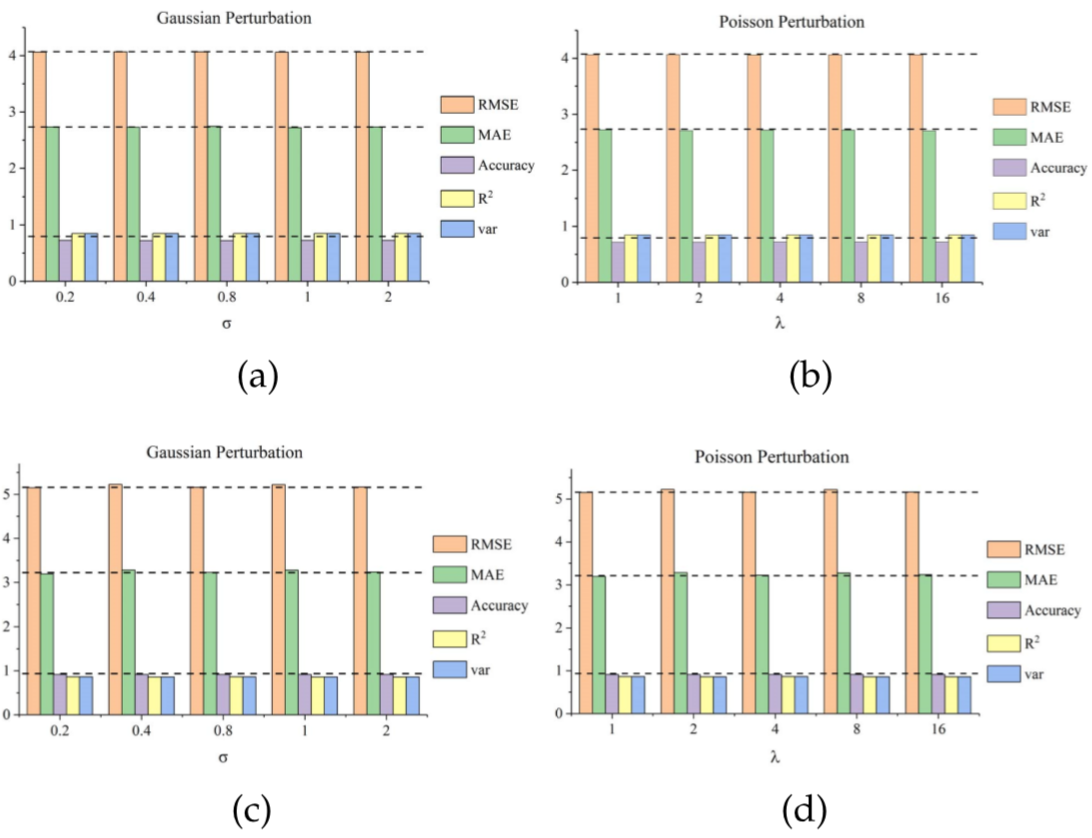
由评估指标的随噪声的变化细微可以得出T-GCN具强鲁棒性的结论。
模型解释:
文章将T-GCN所得的预测结果与真实数据可视化得到结论:
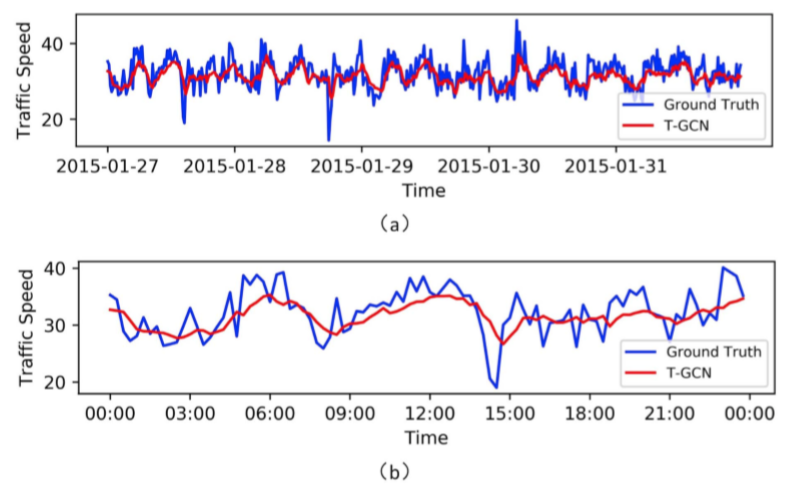
模型对于峰谷值的预测效果不佳,原因在于T-GCN在傅里叶域中定义了平滑过滤器,通过不断移动过滤器提取空间特征,造成了全局预测中的细微变化,使得曲线中的峰变得平滑。
文章还指出预测与实际之间存在固定误差,由数据集的特殊性造成,即SZ-taxi数据集表示某时刻出租车的数量可能为0,但实际道路上车辆的数量不一定为0;
对这篇论文的解读就到这里结束了,Methodology部分使用GCN与GNU的理论,设计了新的计算单元;Experiment部分很让我受教,对实验的条件、前提设定的非常详尽,在介绍数据集与衡量指标后,对选取实验参数作了严格的实验论证;对实验结果进行了详尽的分析,通过与其他几个模型的预测结果进行对比,从空间、时间、时间跨度预测、精度、鲁棒性等角度对模型的优越性进行对比论证,数据的选取与展示都精确地契合了论证的论点;最后关于傅里叶与峰谷偏差的模型解释很精妙。
关于GNU、LSTM的学习解读会继续跟进。同时也会对这篇论文git上的开源代码进行解读与实验复现。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号