Op-level的快速算法

十岁的小男孩

　　本文为终端移植的一个小章节。

引言

　　本节针对CNN进行加速计算的，主要有以下两种方法，FFT和Winograd两种方法。

FFT Conv2d (7x7, 9x9)

　　FFT（Fast Fourier Transformation）是离散傅氏变换（DFT）的快速算法。即为快速傅氏变换。它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。

　　 FFT加速convolution，按照Convolution Theorem，时域上的卷积可以转成空间域的傅立叶变换进行。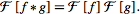

　　lecun的文章就是通过把卷积变成傅立叶变换实现加速的。从实验里看到，加速比2倍左右。目前这部分有代码开源，但是好像并没有merge到caffe中，原因可能是因为加速比例有限，再者消耗空间。猜测主要是加速比例问题吧，因为加速过程中，由于其原理，当卷积核小，是没什么加速的，当核是3或者5时，速度有的更慢或者相当，而在cnn中卷积的核大多数比较小，起到的加速作用很小，而基于图像处理本身目前的任务来说，卷积核一般不会太大，googlenet用7X7已经是爆炸天了。而从另外一方面来说，对caffe实现多GPU卡的加速或者多机的加速，则是实打实的加速，无论你的卷积核多大，你都能加速。

　　lecun他们又出了一篇新的文章，facebook的，Fast Convolutional Nets With fbfft: A GPU Performance Evaluation。caffe上已经有人实现了，加速1.4(3X3)到14.5倍。从他们的文章中看到，卷积核小的时候也是实现了加速了。

　　参考：Duan2baka的博客