Softmax

Softmax

目录

　　1.Softmax概念

　　2.Softmax分类

　　3.Softmax回归

　　4. Softmax 与 SVM

1.Softmat概念

1.1什么是Softmax函数？

　　我们知道max，假如说我有两个数，a和b，并且a>b，如果取max，那么就直接取a，没有第二种可能

但有的时候我不想这样，因为这样会造成分值小的那个饥饿。所以我希望分值大的那一项经常取到，分值小的那一项也偶尔可以取到，那么我用softmax就可以了 现在还是a和b，a>b，如果我们取按照softmax来计算取a和b的概率，那a的softmax值大于b的，所以a会经常取到，而b也会偶尔取到，概率跟它们本来的大小有关。所以说不是max，而是 Soft max 那各自的概率究竟是多少呢，我们下面就来具体看一下

1.1.1Definition：

　　其中，Vi 是分类器前级输出单元的输出。i 表示类别索引，总的类别个数为 C。Si 表示的是当前元素的指数与所有元素指数和的比值。Softmax 将多分类的输出数值转化为相对概率，更容易理解和比较。Softmax 在机器学习和深度学习中有着非常广泛的应用。尤其在处理多分类（C > 2）问题，分类器最后的输出单元需要Softmax 函数进行数值处理。

1.1.2 Example

一个多分类问题，C = 4。线性分类器模型最后输出层包含了四个输出值，分别是：

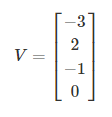
经过Softmax处理后，数值转化为相对概率：

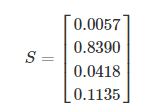
很明显，Softmax 的输出表征了不同类别之间的相对概率。我们可以清晰地看出，S1 = 0.8390，对应的概率最大，则更清晰地可以判断预测为第1类的可能性更大。Softmax 将连续数值转化成相对概率，更有利于我们理解。

实际应用中，使用 Softmax 需要注意数值溢出的问题。因为有指数运算，如果 V 数值很大，经过指数运算后的数值往往可能有溢出的可能。所以，需要对 V 进行一些数值处理：即 V 中的每个元素减去 V 中的最大值。 

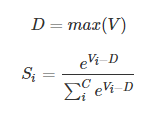
Code：

scores = np.array([123, 456, 789])    # example with 3 classes and each having large scores
scores -= np.max(scores)    # scores becomes [-666, -333, 0]
p = np.exp(scores) / np.sum(np.exp(scores))

1.2 Softmax 损失函数

1.2.1 公式：

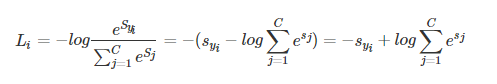
推导：

we know，线性分类器的输出是输入 x 与权重系数的矩阵相乘：s = Wx。对于多分类问题，使用 Softmax 对线性输出进行处理。

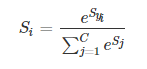
其中，Syi是正确类别对应的线性得分函数，Si 是正确类别对应的 Softmax输出。

由于 log 运算符不会影响函数的单调性，我们对 Si 进行 log 操作：

我们希望 Si 越大越好，即正确类别对应的相对概率越大越好，那么就可以对 Si 前面加个负号，来表示损失函数：

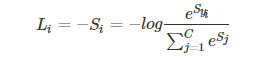
对上式进一步处理，把指数约去：

 

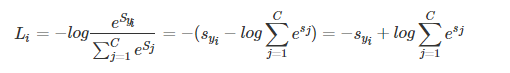
1.2.2 Example

原始数据为：

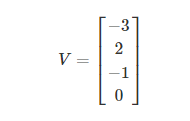
假设 i = 1 为真实样本，计算其损失函数为：

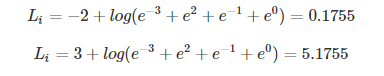
2. Softmax 分类

我们常见的逻辑回归、SVM等常用于解决二分类问题，对于多分类问题，比如识别手写数字，它就需要10个分类，同样也可以用逻辑回归或SVM，只是需要多个二分类来组成多分类，但这里讨论另外一种方式来解决多分类——softmax

定性地来讲，Softmax回归是Logitic回归的拓展。一般而言，Logistic常用于二分类问题上，而Softmax回归则可用于多分类的问题上，比如后面实现的手写数字识别。

这里在使用TensorFlow实现Softmax回归识别手写数字之前，简单地讲解一下Softmax回归的原理。此处讲解以和Logistic回归对比为主。

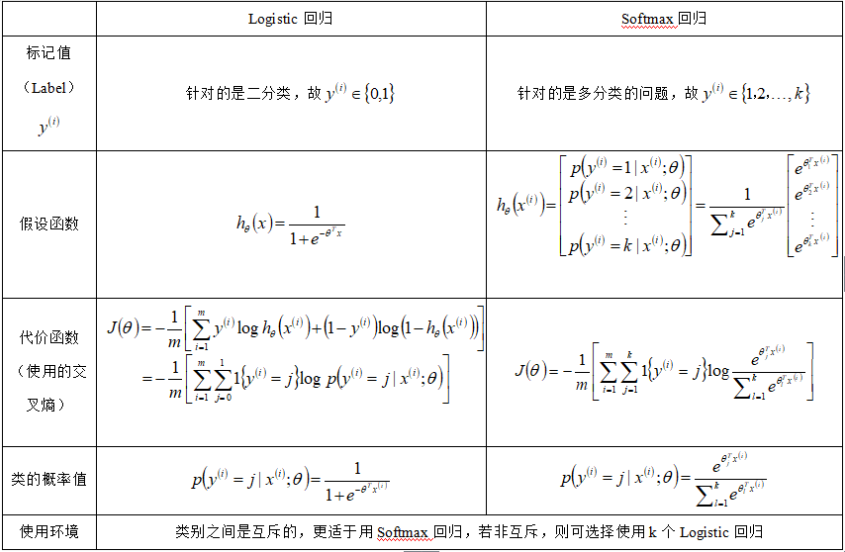
如何多分类？

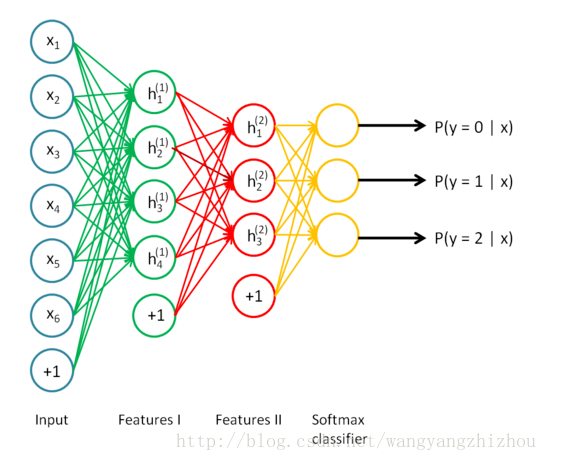
继续看下面的图，三个输入通过softmax后得到一个数组[0.05 , 0.10 , 0.85]，这就是soft的功能。

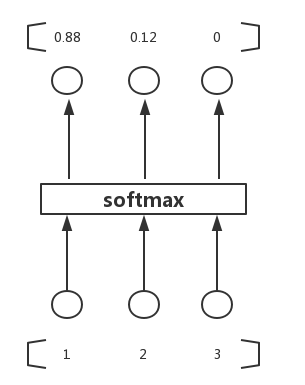
计算过程直接看下图，其中zLiziL即为θTixθiTx，三个输入的值分别为3、1、-3，ezez的值为20、2.7、0.05，再分别除以累加和得到最终的概率值，0.88、0.12、0。

损失函数：

3. Softmax 回归

logistic回归只能输出0和1，一般来说只能进行二分类问题，但是用one-vs-all的技巧也能进行多分类，softmax算是logistic回归的推广，它能直接处理多分类问题 
  softmax函数，或称归一化函数，是逻辑函数的一种推广，它能将一个含任意实数的K维向量压缩到另一个K维实向量中，使得每一个元素范围都在（0，1）之间，并且所有元素的和为1，这样就可以联系到概率上进行多分类问题的求解 
  softmax函数： 

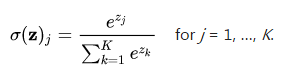
可以推导出softmax的输出结果y对于它的输入数据z的导数 

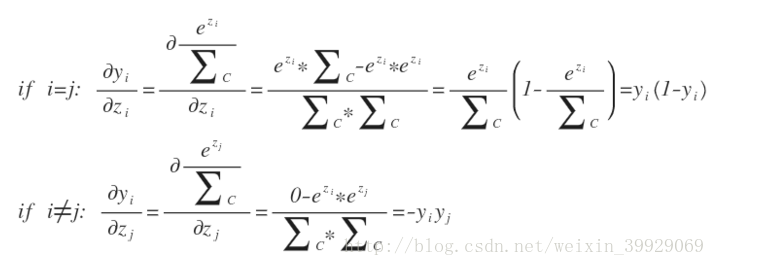
用交叉熵来定义误差函数，其中t是实际概率

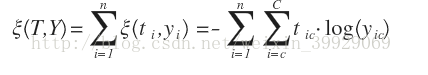
损失函数对输入数据z的导数推导如下 

 

 

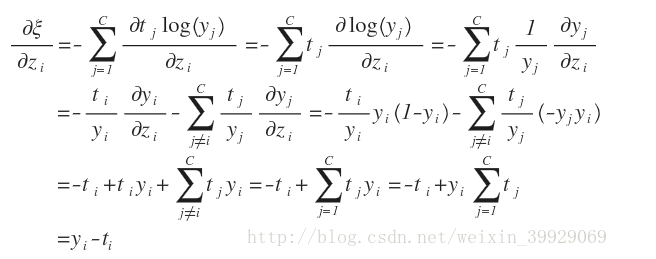
4. Softmax 与 SVM 

Softmax线性分类器的损失函数计算相对概率，又称交叉熵损失「Cross Entropy Loss」。线性 SVM 分类器和 Softmax 线性分类器的主要区别在于损失函数不同。SVM 使用 hinge loss，更关注分类正确样本和错误样本之间的距离「Δ = 1」，只要距离大于 Δ，就不在乎到底距离相差多少，忽略细节。而 Softmax 中每个类别的得分函数都会影响其损失函数的大小。举个例子来说明，类别个数 C = 3，两个样本的得分函数分别为[10, -10, -10]，[10, 9, 9]，真实标签为第0类。对于 SVM 来说，这两个 Li 都为0；但对于Softmax来说，这两个 Li 分别为0.00和0.55，差别很大。

关于 SVM 线性分类器，原博主在上篇文章里有所介绍，传送门：

基于线性SVM的CIFAR-10图像集分类

接下来，谈一下正则化参数 λ 对 Softmax 的影响。我们知道正则化的目的是限制权重参数 W 的大小，防止过拟合。正则化参数 λ 越大，对 W 的限制越大。例如，某3分类的线性输出为 [1, -2, 0]，相应的 Softmax 输出为[0.7, 0.04, 0.26]。假设，正类类别是第0类，显然，0.7远大于0.04和0.26。

若使用正则化参数 λ，由于限制了 W 的大小，得到的线性输出也会等比例缩小：[0.5, -1, 0]，相应的 Softmax 输出为[0.55, 0.12, 0.33]。显然，正确样本和错误样本之间的相对概率差距变小了。

也就是说，正则化参数 λ 越大，Softmax 各类别输出越接近。大的 λ 实际上是「均匀化」正确样本与错误样本之间的相对概率。但是，概率大小的相对顺序并没有改变，这点需要留意。因此，也不会影响到对 Loss 的优化算法。

完。