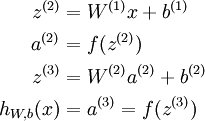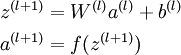神经网络,前向传播FP和反向传播BP
1 神经网络
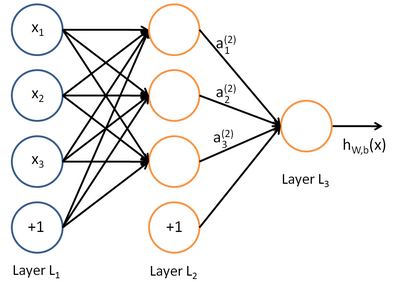
神经网络就是将许多个单一“神经元”联结在一起,这样,一个“神经元”的输出就可以是另一个“神经元”的输入。例如,下图就是一个简单的神经网络:
我们使用圆圈来表示神经网络的输入,标上“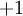 ”的圆圈被称为偏置节点,也就是截距项。神经网络最左边的一层叫做输入层,最右的一层叫做输出层(本例中,输出层只有一个节点)。中间所有节点组成的一层叫做隐藏层,因为我们不能在训练样本集中观测到它们的值。同时可以看到,以上神经网络的例子中有3个输入单元(偏置单元不计在内),3个隐藏单元及一个输出单元。
”的圆圈被称为偏置节点,也就是截距项。神经网络最左边的一层叫做输入层,最右的一层叫做输出层(本例中,输出层只有一个节点)。中间所有节点组成的一层叫做隐藏层,因为我们不能在训练样本集中观测到它们的值。同时可以看到,以上神经网络的例子中有3个输入单元(偏置单元不计在内),3个隐藏单元及一个输出单元。
我们用 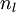 来表示网络的层数,本例中
来表示网络的层数,本例中 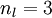 ,我们将第
,我们将第  层记为
层记为 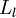 ,于是
,于是 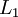 是输入层,输出层是
是输入层,输出层是 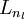 。本例神经网络有参数
。本例神经网络有参数 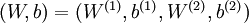 ,其中
,其中 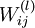 (下面的式子中用到)是第
(下面的式子中用到)是第  层第
层第  单元与第
单元与第  层第
层第  单元之间的联接参数(其实就是连接线上的权重,注意标号顺序),
单元之间的联接参数(其实就是连接线上的权重,注意标号顺序), 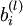 是第
是第  层第
层第  单元的偏置项。因此在本例中,
单元的偏置项。因此在本例中, 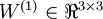 ,
, 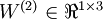 。注意,没有其他单元连向偏置单元(即偏置单元没有输入),因为它们总是输出
。注意,没有其他单元连向偏置单元(即偏置单元没有输入),因为它们总是输出 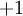 。同时,我们用
。同时,我们用 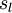 表示第
表示第  层的节点数(偏置单元不计在内)。
层的节点数(偏置单元不计在内)。
2 前向传播FP
我们用 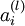 表示第
表示第  层第
层第  单元的激活值(输出值)。当
单元的激活值(输出值)。当 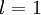 时,
时, 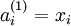 ,也就是第
,也就是第  个输入值(输入值的第
个输入值(输入值的第  个特征)。对于给定参数集合
个特征)。对于给定参数集合 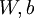 ,我们的神经网络就可以按照函数
,我们的神经网络就可以按照函数 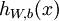 来计算输出结果。本例神经网络的计算步骤如下:
来计算输出结果。本例神经网络的计算步骤如下:
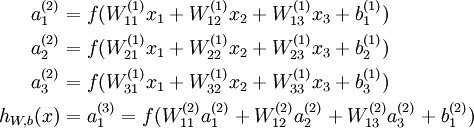
我们用 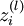 表示第
表示第  层第
层第  单元输入加权和(包括偏置单元),比如,
单元输入加权和(包括偏置单元),比如, 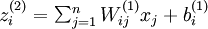 ,则
,则 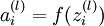 。
。
这样我们就可以得到一种更简洁的表示法。这里我们将激活函数 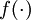 扩展为用向量(分量的形式)来表示,即
扩展为用向量(分量的形式)来表示,即 ![\textstyle f([z_1, z_2, z_3]) = [f(z_1), f(z_2), f(z_3)]](http://ufldl.stanford.edu/wiki/images/math/d/b/8/db84346dcd6187f0fbb0f6c1a72eecf8.png) ,那么,上面的等式可以更简洁地表示为:
,那么,上面的等式可以更简洁地表示为:
我们将上面的计算步骤叫作前向传播。回想一下,之前我们用 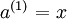 表示输入层的激活值,那么给定第
表示输入层的激活值,那么给定第  层的激活值
层的激活值 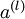 后,第
后,第  层的激活值
层的激活值 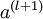 就可以按照下面步骤计算得到:
就可以按照下面步骤计算得到:
将参数矩阵化,使用矩阵-向量运算方式,我们就可以利用线性代数的优势对神经网络进行快速求解。
目前为止,我们讨论了一种神经网络,我们也可以构建另一种结构的神经网络(这里结构指的是神经元之间的联接模式),也就是包含多个隐藏层的神经网络。最常见的一个例子是 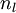 层的神经网络,第
层的神经网络,第 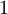 层是输入层,第
层是输入层,第 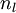 层是输出层,中间的每个层
层是输出层,中间的每个层  与层
与层  紧密相联。这种模式下,要计算神经网络的输出结果,我们可以按照之前描述的等式,按部就班,进行前向传播,逐一计算第
紧密相联。这种模式下,要计算神经网络的输出结果,我们可以按照之前描述的等式,按部就班,进行前向传播,逐一计算第 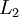 层的所有激活值,然后是第
层的所有激活值,然后是第 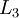 层的激活值,以此类推,直到第
层的激活值,以此类推,直到第 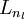 层。这是一个前馈神经网络的例子,因为这种联接图没有闭环或回路。
层。这是一个前馈神经网络的例子,因为这种联接图没有闭环或回路。
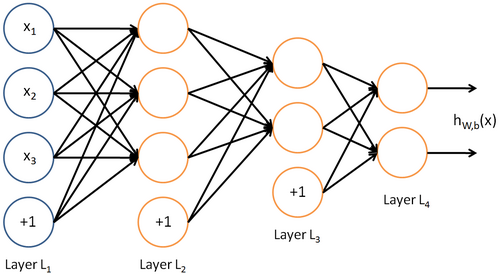
神经网络也可以有多个输出单元。比如,下面的神经网络有两层隐藏层: 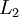 及
及 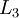 ,输出层
,输出层 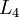 有两个输出单元。
有两个输出单元。
要求解这样的神经网络,需要样本集 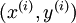 ,其中
,其中 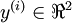 。如果你想预测的输出是多个的,那这种神经网络很适用。(比如,在医疗诊断应用中,患者的体征指标就可以作为向量的输入值,而不同的输出值
。如果你想预测的输出是多个的,那这种神经网络很适用。(比如,在医疗诊断应用中,患者的体征指标就可以作为向量的输入值,而不同的输出值 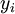 可以表示不同的疾病存在与否。)
可以表示不同的疾病存在与否。)
3 反向传播BP
前面用初始化的联结权重计算的输出层值和实际值肯定会有很大的偏差,我们需要对连接权重进行优化,此时就需要使用反向传播算法。
现在假设经过前向传播算法计算的某个输出值为ykyk,表示输出层的第kk个输出,而其实际的值为tktk(训练样本的标签值是已知的,不然怎么训练)。那么误差函数定义如下:

后向传播算法是通过梯度下降的方法对联结权重进行优化,所以需要计算误差函数对联结权重的偏导数。
1.计算总误差
总误差:(square error)
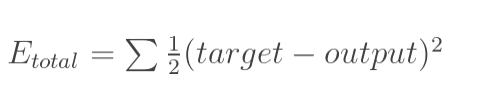
但是有两个输出,所以分别计算o1和o2的误差,总误差为两者之和:


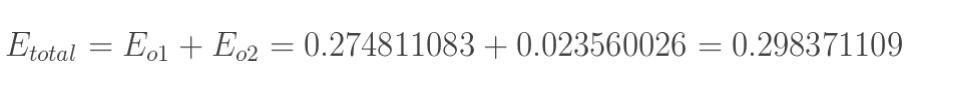
2.隐含层---->输出层的权值更新:
以权重参数w5为例,如果我们想知道w5对整体误差产生了多少影响,可以用整体误差对w5求偏导求出:(链式法则)

下面的图可以更直观的看清楚误差是怎样反向传播的: