损失函数(交叉熵 均方误差)
损失函数
Question?
是什么?
有什么用?
怎么用?
1 是什么?
损失函数(loss function)是用来估量你模型的预测值f(x)与真实值Y的不一致程度,它是一个非负实值函数,通常使用L(Y, f(x))来表示,损失函数越小,模型的鲁棒性就越好。损失函数是经验风险函数的核心部分,也是结构风险函数重要组成部分。模型的结构风险函数包括了经验风险项和正则项,通常可以表示成如下式子:
其中,前面的均值函数表示的是经验风险函数,L代表的是损失函数,后面的Φ
2 有什么用?
损失函数是用来度量预测值与真实值之间的差异.损失函数通常写做L(y_,y).y_代表了预测值,y代表了真实值. 目标函数可以看做是优化目标,优化模型的最后目标就是使得这个目标函数最大或者最小. 代价函数类似于目标函数. 区别:目标函数(代价函数)可以包含一些约束条件如正则化项.
3 怎么用?
传统损失函数
监督学习的两大类
-
分类问题:将不同的样本划分到已知的类别当中
多分类中,神经网络对每个样本产生一个n维数组作为输出结果,代表每个样本属于各类别的可能性。当然,如果是one-hot coding,那么输出应该只有所属类别的维度值是1,在其余类别的维度是0.
如何判断输出y与真实值y_truth有多接近?
常用方法:交叉熵cross_entropy,它描述了两个概率分布之间的距离,当交叉熵越小说明二者之间越接近
交叉熵定义,概率qq表示概率pp的交叉熵为:
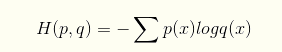
cross_entropy = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0))) # y_:真实值,y:原始输出 # tf.reduce.mean函数求解平均数 # tf.clip_by_value函数将一个张量的数值限制在一个范围内,上面代码将 q 的值限制在(1e-10, 1.0)之间
v=tf.constant([[1.0,2.0,3.0],[4.0,5.0,6.0]])
with tf.Session() as sess:
print(tf.clip_by_value(v,2.5,4.5).eval())
'''
输出为
[[ 2.5 2.5 3. ]
[ 4. 4.5 4.5]]
'''
# tensorflow中提供的直接计算交叉熵损失的函数,y代表神经网络的输出结果,y_表示真实类别
cross_entropy=tf.nn.softmax_cross_entropy_with_logits(logits=y,y_)
但是,网络的输出不一定是概率分布,因此需要将网络前向传播的结果转换成概率分布。常用方法是Softmax回归.tensorflow中,Softmax回归只作为一层额外的处理层,进行概率分布的转换。转换公式:
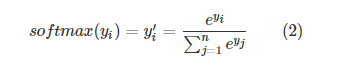
式中原始的网络输出是yiyi,y′iyi′是转换后的概率分布。注意的是公式(1)并不是对称的,也即是(H(p,q))≠H(q,p)(H(p,q))≠H(q,p),公式(1)描述的是概率qq表达概率pp的困难程度。因此在神经网络的损失函数中,qq代表预测值,pp代表真实值。tensorflow将cross_entropy与softmax统一封装实现了softmax后的cross_entropy损失函数
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(y, y_)
- 回归问题:对具体数值的预测
如房价预测、销量预测等问题需要预测的是一个任意实数,其网络输出只有一个节点,也即是预测值。
常用的损失函数:均方误差(MSE, mean squared error)
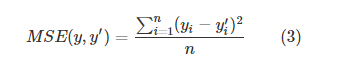
其中batch中的第i个输入的正确值记作yi,其预测值记作y′i mse = tf.reduce.mean(tf.squared(y_ - y)) # y_:正确值,y:预测值
自定义损失函数
自定义的损失函数通常更加符合所应用的场景,如在销量预测中,我们对预测值与正确值之间的大小关系作为损失调整的条件,那么得到类似下面的式子:
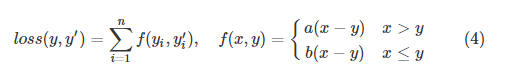
loss = tf.reduce.sum(tf.select(tf.greater(v1, v2), a*(v1-v2), b*(v1-v2))) # a>b时,m=True,否则m=False m = tf.greater(a, b) # m=True时,执行func1;m=False时,执行func2 tf.select(m, func1, func2)

