logistic回归原理
一、logistic回归和线性回归的关系
想必大家也早有疑惑,既然logistic回归名字中都带有“回归”二者,难道和回归模型一点关系都没有!没错,二者是有联系的,下面我们便来谈一谈!
首先给出线性回归模型:
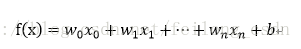
写成向量形式为:
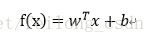
同时“广义线性回归”模型为:
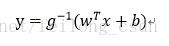
注意,其中g(~)是单调可微函数。
下面我们便从线性回归的回归模型引出logistic回归的分类模型!!!
我们知道上诉线性回归模型只能够进行回归学习,但是若要是做分类任务如何做!答案便是在“广义线性回归”模型中:只需找一个单调可微函数将分类任务的真实标记y与线性回归模型的预测值联系起来便可以了!
logistic回归是处理二分类问题的,所以输出的标记y={0,1},并且线性回归模型产生的预测值z=wx+b是一个实值,所以我们将实值z转化成0/1值便可,这样有一个可选函数便是“单位阶跃函数”:
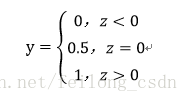
这种如果预测值大于0便判断为正例,小于0则判断为反例,等于0则可任意判断!
但是单位阶跃函数是非连续的函数,我们需要一个连续的函数,“Sigmoid函数”便可以很好的取代单位阶跃函数:
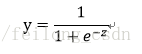
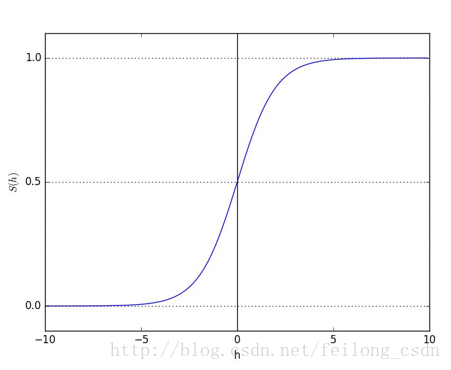
sigmoid函数在一定程度上近似单位阶跃函数,同时单调可微,图像如下所示:
这样我们在原来的线性回归模型外套上sigmoid函数便形成了logistic回归模型的预测函数,可以用于二分类问题:
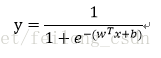
对上式的预测函数做一个变换为:
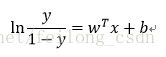
观察上式可得:若将y视为样本x作为正例的可能性,则1-y便是其反例的可能性。二者的比值便被称为“几率”,反映了x作为正例的相对可能性,这也是logistic回归又被称为对数几率回归的原因!
这里我们也便可以总结一下线性回归模型和logistic回归的关系:
logistic回归分类模型的预测函数是在用线性回归模型的预测值的结果去逼近真实标记的对数几率!这样也便实现了上面说的将线性回归的预测值和分类任务的真实标记联系在了一起!
二、梯度上升算法求解logistic回归模型参数w
在上一个话题中我们已经得到了logistic回归的预测函数:

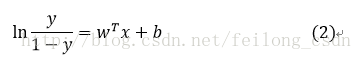
这里我们将式子中的y视为类后验概率估计p(y=1|x),则上式可以重写为:
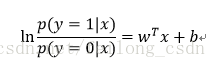
求解上式有:
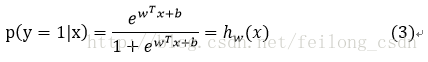
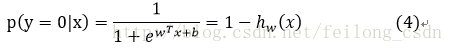
先给出求解参数w的思路,下面我们便按照这个思路进行求解参数w:
1、为求解参数w,我们需要定义一个准则函数 J(w),利用准则函数求解参数w
2、我们通过最大似然估计法定义准则函数J(w)
3、接下来通过最大化准则函数J(w)便可求出参数w的迭代表达式
4、为了更好地使用数据求出参数w,我们将第三步得到的w的迭代时向量化。自此便完成了对于参数w的推导过程,接下来便可以进行实例应用了!
步骤一、求解准则函数J(w)
合并(3)(4)两个式子可得:
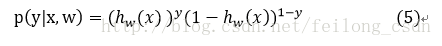
在(5)式中y={0,1},是个二分类问题,所以y只是取两个值0或是1。
根据(5)式可得似然函数为:
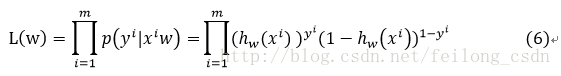
对(6)式取对数有:
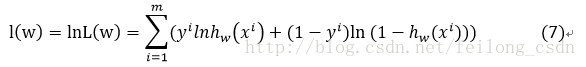
因此定义准则函数为:
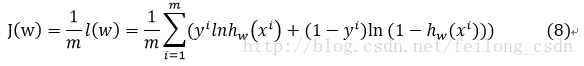
最终我们的目标便是最大化似然函数,也就是最大化准则函数:

步骤二、梯度上升算法求解参数w
这里我们使用梯度上升算法求解参数w,因此参数w的迭代式为:
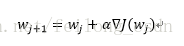
其中α是正的比例因子,用于设定步长的“学习率”
其中对准则函数J(w)进行微分可得:
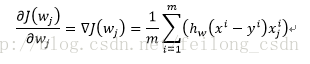
所以得到最终参数w的迭代式为:
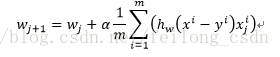
上式将(1/m)去掉不影响结果,等价于下式:
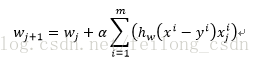
至此我们已经得出了w的迭代公式,按说是可以在引入数据的情况下进行w的计算,进而进行分类!但是数据基本都是以矩阵和向量的形式引入的,所以我们需要对上面w的迭代时进行向量化,以方便实例应用中的使用。
步骤三、w迭代公式向量化
首先对于引入的数据集x来说,均是以矩阵的形式引入的,如下:
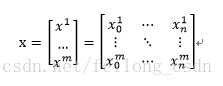
其中m数据的个数,n是数据的维度,也就是数据特征的数量!
再者便是标签y也是以向量的形式引入的:
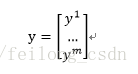
参数w向量化为:
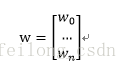
在这里定义M=x*w,所以:
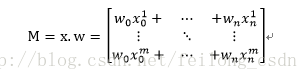
定义上面说的sigmoid函数为:
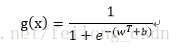
所以定义估计的误差损失为:
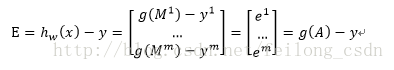
在此基础上,可以得到步骤二中得到的参数迭代时向量化的式子为:

原文出处:https://blog.csdn.net/feilong_csdn/article/details/64128443
感谢该博主,借鉴摘录为后续复习留档。

