查找漫谈，从布隆过滤器到分布式一致性缓存

查找的需求背景

在日常开发过程中，我们经常需要用到查找这个功能。
如：

用户在配置文件中下发了一系列过滤规则，如何确定文件中某条规则是否已经下发过了
注册模块中，查看某用户的用户名和密码是注册过的
网络爬虫程序，如何不去爬相同的url界面
。。。。。。等等

使用简单的数据结构

比较简单的方式是建立一个查找效率高的数据结构，每次加载时都检查本条数据是否已经处理过。未处理过则加入到数据结构中，处理过则进行相应处理。

常用的高效查找的数据结构有以下几种：

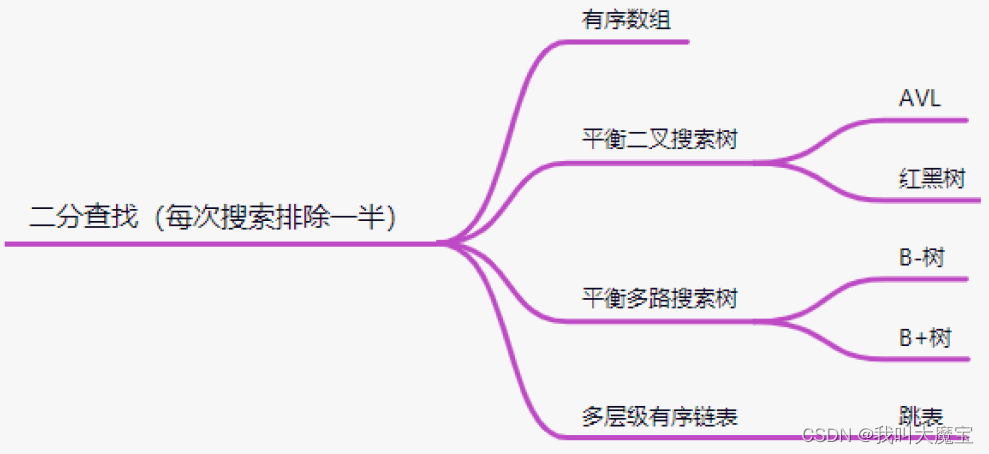
这些数据结构（内部数据有序）的查找时间复杂度都为O（log₂n），原因就是每次查找都能排除一半的数据，n为查找次数，原则上2^n 大于查找的数据集大小，就可以完成目标的查找。

使用哈希表

不少朋友也喜欢使用哈希表进行数据的存储于查找，谈到哈希表就需要确定key-value的形式。在这种场景下，我们可以让查找内容做key，存在结果为value；

哈希表的基本原理：

将key通过带入哈希函数中进行散列运算，即hash（key）= index，
通过index定位到该key的存储位置，将key-value的绑定关系存到该index下的node中。
当hash（key_1）= hash(key_2)时，我们一般称key_1与key_2发生了冲突（哈希碰撞）;

哈希函数的选型

哈希函数有以下要义：

计算速度快
强随机分布（等概率的分布到所有地址空间）

现在常用的hash函数有以下几种：

murmurhash1（计算速度快，但是随机分布性较差）
murmurhash2（计算速度适中，但是随机分布性适中，常用）
murmurhash3（计算速度慢，但是随机分布性较好）
siphash（redis6.0，rust中hashmap的实现，主要用于解决字符串相近的强随机分布性）
cityhash（大规模分布式系统中得到了广泛应用）

哈希碰撞的解决

负载因子

负载因子= 已储存节点数 / 总结点数；用来形容哈希表的储存密度，
负载因子越大，越容易产生哈希碰撞。

解决办法

链表法

链表法是传统桶链式哈希表的常用方法，将碰撞后的节点存入该index对应的链表后。
值得一提的是，当冲突的元素较多，造成后面的链表过长，链表可以转换成红黑树或者最小堆，
从而降低时间复杂度。按照java中hashmap的习惯，后方链表节点数超过256后采用该转换方法。

开放寻址法

将所有的元素都存入表中，当出现哈希碰撞时，加一定步长进行再次查找，
如

i + 1, i + 2, i + 3, i + 4, ...,i+n;
i - 1, i + 2^2, i - 3^2 ,i + 4^2,
双重hash，将index再次hash散列到别的index

其中1，2方法会将hash值的结果聚集到某一块区域，不符合均匀分布的要求，所以称之为hash聚集，3的方法可以规避哈希聚集；

布隆过滤器

布隆过滤器

定义

布隆过滤器是一种概率性数据结构，它的特点是高效的插入和查询操作，能确定一个字符串一定存在或者可能存在。
布隆过滤器不存储具体数据，所以占用空间小；查询结果存在误差，但是误差可控，同时不支持删除操作；

应用场景

布隆过滤器通常用于判断某个 key 一定不存在的场景，同时允许判断存在时有误差的情况；
常见处理场景：

缓存穿透的解决
热key限流

原理

布隆过滤器主体采用位图 + n个哈希函数构成；

位图

以一个8bit位图举例。
比如存在一个八字节的内存块（内存已清空），其逻辑空间可以看做一个8*8位的正方形空间。我们的key经过一次哈希运算后，假设运算出的哈希值为173，该值可以映射到该位图空间中的一个位点。

寻找该哈希值在位图中对应的位置可经过如下运算：

173 % （2 ^ 8） = 173 &  （2 ^ 8 - 1） = 45；
45 % 8 = 5； //计算x轴坐标
45 / 8 = 5；	// 计算y轴坐标

最终计算得到173对应到位图中的坐标为（5,5）；
再经过n次hash运算，可以在位图中确定n个该key所对应的位图坐标。
比如经过四轮确定的hash函数，我们就可以在位图中确定该key对应的四个位点，并将该4位置一；

后期检索时，对要检查的key进行n轮hash运算并查看对应的位点是否置1，如果有一个点不为1，则该key一定没存过。如果全都为1，则该key可能存进去过。为什么说可能？因为某个本没存过的key可能访问到了其他key“点亮”了的位点，导致错误的判断。不过该概率是可控的，我们称发生这个的概率为假阳率；

同时我们也可以理解为什么布隆过滤器的删除非常困难，因为某个位点可以被多次设置为1，同时不知道被哪个hash函数映射而来；

布隆过滤器遵守的规则

n -- 预期布隆过滤器中元素的个数，如上图 只有str1和str2 两
个元素 那么 n=2
p -- 假阳率，在0-1之间 0.000000
m -- 位图所占空间
k -- hash函数的个数
公式如下：
n = ceil(m / (-k / log(1 - exp(log(p) / k))))
p = pow(1 - exp(-k / (m / n)), k)
m = ceil((n * log(p)) / log(1 / pow(2, log(2))));
k = round((m / n) * log(2));

确定n和p：
在实际使用布隆过滤器时，首先需要确定 n 和 p，通过上面的运算得出 m 和 k；通常可以在下面这个网站上选出合适的值；
https://hur.st/bloomfilter

分布式一致性hash

定义

分布式一致性 hash 算法将哈希空间组织成一个虚拟的圆环，圆环的大小是 2^32；
负载均衡时，我们一般会根据数据数据特征对应的一个数值去映射到对应的处理器；如处理网络数据流时，我们根据这个数据的hash（五元组数值）% 2^32 得出一个介于[0,2^32)的数值，通过这个数值顺时针查找到该数据对应的服务器id;

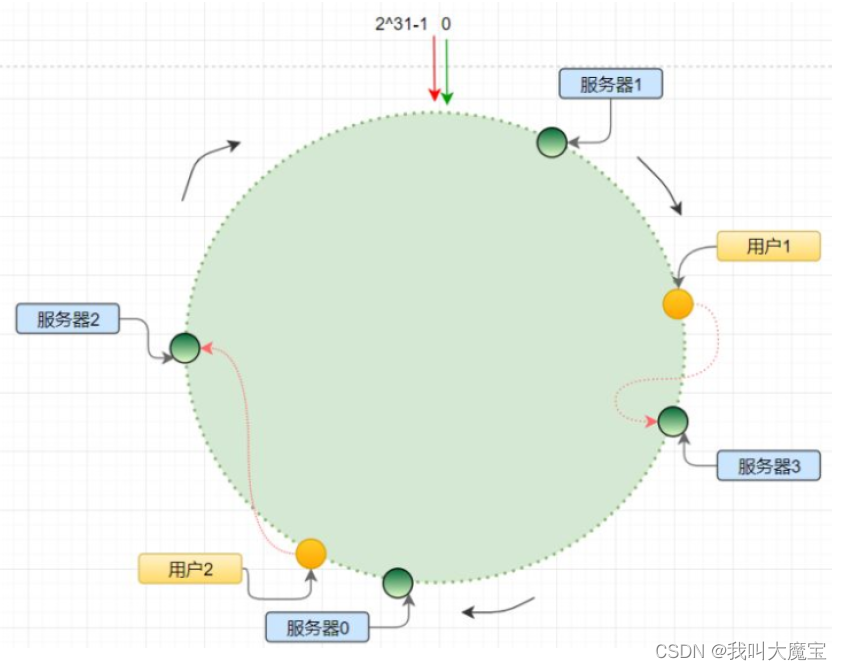
哈希偏移

但是hash算法的结果可能是不均匀分布的，不均匀分布的数值会引起数据的不均匀分配，服务器承受的压力也会不均匀(哈希偏移)，同时环上某个服务器宕机或者新增，会加剧负载分布不均；

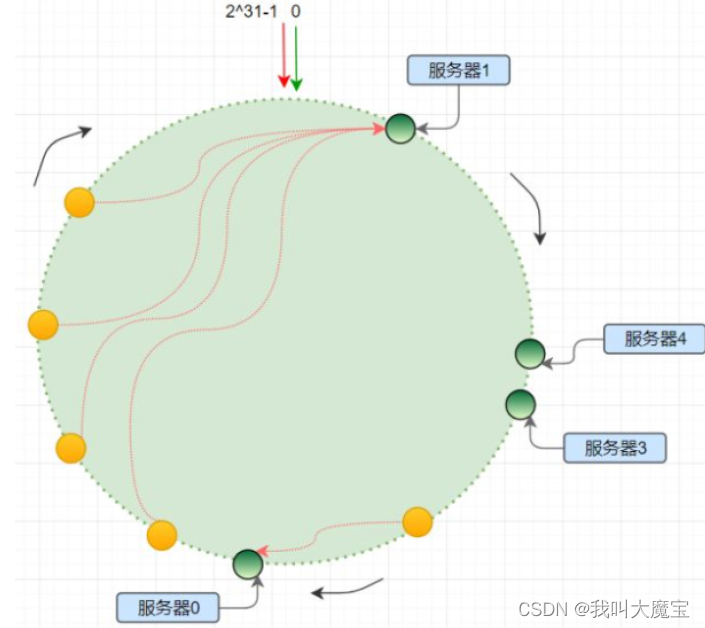
解决办法

为了解决哈希偏移的问题，增加了虚拟节点的概念；理论上，哈希环上节点数越多，数据分布越均衡；为每个服务节点计算多个哈希节点（虚拟节点）；通常做法是， hash("IP:PORT:seqno")，这样实际工作的服务器就会均匀分散到哈希环上，避免哈希偏移；

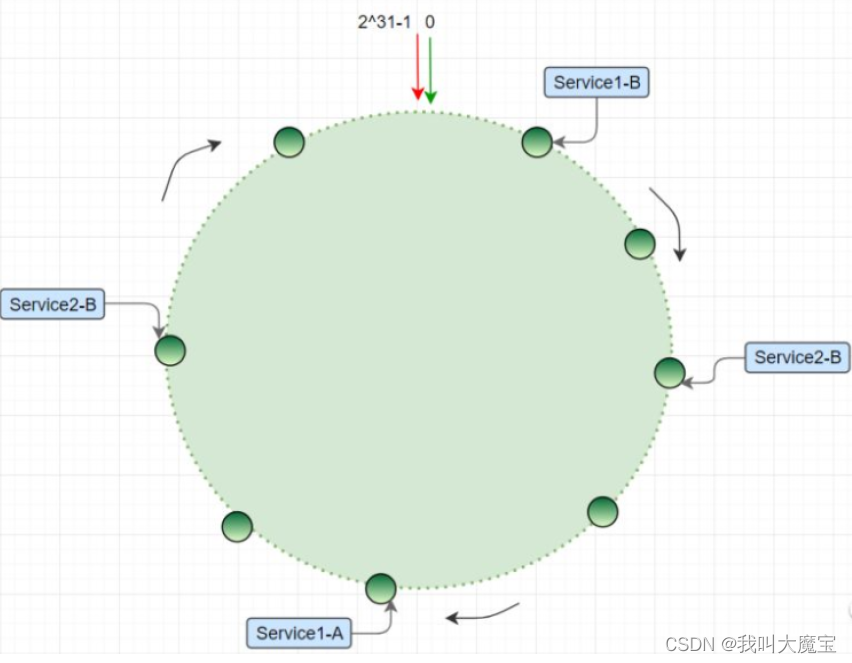
分布式一致性 hash 增加或者删除节点怎么进行数据迁移？
参考：https://github.com/metang326/consistent_hashing_cpp