matlab学习记（一）矩阵

为了不拖数模小队【魏公村汽配维修站良乡分站数模岗】的后腿而被他们踢出去 开始学一学matlab
先占个坑，晚上近现代史再搞

1.m文件：
类似于封装函数，m文件名为函数名，以function f(x)开始，保存后可以在命令行中调用该函数
2.数组：
构造：

x=[1,2,3,4,5,6];%无分号就会直接输出左值
x=[1,2,3;4,5,6];%用分号换行构造二维数组
x=m:k:n%从m到n的一维数组，步长为k
x=linspace(m,n,k)%从m到n有k+1个元素

四则运算：

%数组与数 x=[a,b,c,d,e],q;
x+q=[a+q,b+q,c+q,d+q,e+q];
x-q=[a-q,b-q,c-q,d-q,e-q];
x*q=[a*q,b*q,c*q,d*q,e*q];
x/q=[a/q,b/q,c/q,d/q,e/q];
x\.q=[q/a,q/b,q/c,q/d,q/e];
x^q=[a^q,b^q,c^q,d^q,e^q];
q.^x=[q^a,q^b,q^c,q^d,q^e];

%数组与数组

(好吧再列举有点蠢：数组之间乘除法，乘方已有定义，会被当成矩阵，因此需要加上.用来重构，/是左除右，\是右除左)
3.矩阵
1)特殊矩阵

a=eye(m,n)%单位矩阵
b=zeros(m,n)%零矩阵
c=ones(m,n)%全一矩阵
d=rand(m,n)%0-1区间随机矩阵
e=randn(m.n)%均值为0，方差为1的标准正态分布随机矩阵
%缺省一个参数时默认为方阵
b=zeros(m);
b=zeros(size(A)) % 和A矩阵相同大小

2.魔方矩阵
n阶魔方阵由1，2，...$n^2$组成，每一行，列，对角线上各n个元素之和都相等=$1+2+...+n^2=\frac{n+n^3}{2}$
n>2时有多种魔方阵，magic(n)产生一个特定的魔方阵

>> m=magic(8);
>> sum(m(1,:))

ans =

   260

>> sum(m(:,1))

ans =

   260

3.范德蒙方阵
对于向量v=[v1,v2,...,vn],范德蒙矩阵的一般形式为：倒数第i列是v的i-1次方，范德蒙矩阵常用在各种通信系统的纠错编码中

3.希尔伯特矩阵

n阶希尔伯特矩阵一般形式为h(i,j)=$\frac{1}{i+j-1}$

>> format rat
>> h=hilb(4)

h =

       1              1/2            1/3            1/4     
       1/2            1/3            1/4            1/5     
       1/3            1/4            1/5            1/6     
       1/4            1/5            1/6            1/7     

>> 

4.伴随矩阵

设多项式p(x)为$a_{n}x^{n}+a_{n-1}x^{n-1}+..+a_{1}x+a0$,其伴随矩阵为第一行为an-1~a0/an;其他行是一个少一行的单位矩阵

>> p=[1,-2,-5,6];
>> a=compan(p)

a =

       2              5             -6       
       1              0              0       
       0              1              0       

>> 

伴随矩阵的特征值等于多项式方程的根

5.帕斯卡矩阵

把二项式系数依次填写在矩阵的左侧对角线上

帕斯卡矩阵的逆矩阵各元素也是整数

>> format rat
>> p=pascal(5)

p =

       1              1              1              1              1       
       1              2              3              4              5       
       1              3              6             10             15       
       1              4             10             20             35       
       1              5             15             35             70       

>> inv(p)

ans =

       5            -10             10             -5              1       
     -10             30            -35             19             -4       
      10            -35             46            -27              6       
      -5             19            -27             17             -4       
       1             -4              6             -4              1       

>> 

2)矩阵分块

a[i:j,m:n]%提取a矩阵中i~j行，m~n列的子矩阵
a[:,m:n]%没有数默认为矩阵的边界

3)矩阵合并

%a,b为两矩阵
[a b]a左b右
[a;b]a上b下

4)矩阵运算

a+b
a*b
det(a) % a的行列式
inv(a) % a的逆矩阵
a/b % a*inv(b)
a\b % b*inv(a)

1.提取矩阵的对角线元素

diag(A):矩阵a主对角线元素，产生一个列向量

diag(A,k)：提取a第k条对角线的元素，产生一个列向量（与主对角线平行，向上依次为第一条，第二条）

2.构造对角矩阵

diag(V):构造以向量V为主对角线元素的对角矩阵。

diag(V,k):构造以向量V为第k条对角线元素的对角矩阵

eg.先建立5*5矩阵A，然后将A的第一行元素乘以1，第二行乘以2，...第五行乘以5

>> A=[7,0,1,0,5;3,5,7,4,1;4,0,3,0,2;1,1,9,2,3;1,8,5,2,9]

A =

       7              0              1              0              5       
       3              5              7              4              1       
       4              0              3              0              2       
       1              1              9              2              3       
       1              8              5              2              9       

>> d=diag(1:5);
>> d*A

ans =

       7              0              1              0              5       
       6             10             14              8              2       
      12              0              9              0              6       
       4              4             36              8             12       
       5             40             25             10             45       

每一列乘以i的话可以右乘

3.三角阵

上/下三角阵

上三角阵：triu(A):提取矩阵A的主对角线及以上的元素

triu（A，k）：提取矩阵A的第k条对角线即以上的元素

>> triu(ones(4),-1)

ans =

       1              1              1              1       
       1              1              1              1       
       0              1              1              1       
       0              0              1              1       

tril下三角矩阵

4.矩阵的转置

转置运算符是(.')

共轭转置（’）在转置的基础上取每个数的复共轭

>> a=[1,3;3+4i,1-2i]

a =

       1        +    0i             3        +    0i      
       3        +    4i             1        -    2i      

>> a.'

ans =

       1        +    0i             3        +    4i      
       3        +    0i             1        -    2i      

>> a'

ans =

       1        +    0i             3        -    4i      
       3        +    0i             1        +    2i      

>> 

5.矩阵的旋转

rot90(A,k):将矩阵A逆时针方向旋转90°的k倍

A=[1,3,2;-3,2,1;4,1,2]

A =

       1              3              2       
      -3              2              1       
       4              1              2       

>> rot90(A)

ans =

       2              1              2       
       3              2              1       
       1             -3              4       

>> rot90(A,2)

ans =

       2              1              4       
       1              2             -3       
       2              3              1       

6.矩阵的反转

对矩阵实施左右旋转是将原矩阵的第一列与最后一列调转，以此类推

fliplr(A):左右翻转

flipud(A):上下翻转

eg.验证魔方阵的主对角线，副对角线元素之和相等

>> a=magic(5);
>> d1=diag(a);
>> sum(d1)

ans =

      65       
>> b=flipud(a);
>> d2=diag(b);
>> sum(d2)

ans =

      65       

>> 

7.矩阵的秩

rank(k)

eg.求3~20阶魔方阵的秩

>> for n=3:20
r(n)=rank(magic(n));
end
>> bar(r)
>> grid on
>> axis([2,21,0,20])
>> [3:20;r(3:20)]

ans =

  列 1 至 6

       3              4              5              6              7              8       
       3              3              5              5              7              3       

  列 7 至 12

       9             10             11             12             13             14       
       9              7             11              3             13              9       

  列 13 至 18

      15             16             17             18             19             20       
      15              3             17             11             19              3       

>> 

观察表格可得：奇数阶魔方阵秩为n,为满秩矩阵

n%2==0&&n%4!=0时 秩为n/2+2

n%4==0时秩为3

8.矩阵的迹

矩阵的迹等于矩阵的对角线元素之和，也等于矩阵的特征值之和

trace(A)

>> a=[1,3,2;-3,2,1;4,1,2]

a =

     1     3     2
    -3     2     1
     4     1     2

>> b=trace(a)

b =

     5

>> t=sum(diag(a))

t =

     5

>>

9.向量和矩阵的范数

用来度量矩阵或向量在某种意义上的长度

向量的3种常用范数：

1）向量1范数：向量元素的绝对值之和 norm(v) / norm(v,2)

2）向量2范数：向量元素绝对值的平方和的平方根 norm(v,1)

3）向量无穷范数：所有向量元素绝对值中的最大值 norm(v,inf)

矩阵的3种常用范数：

1）矩阵1范数：所有矩阵列元素绝对值之和的最大值

2)矩阵2范数：A‘ A矩阵的最大特征值的平方根

3）矩阵无穷函数：所有矩阵行元素绝对值之和的最大值

10.矩阵的条件数

矩阵的条件数等于a的范数与a的逆矩阵的范数的乘积

条件数越接近于1，矩阵的性能越好，反之，矩阵性能越差

cond(a,1) / cond(a,inf)...

eg.求2~10阶希尔伯特矩阵的条件数

for n=2:10
c(n)=cond(hilb(n));
end
>> format long
>> c'

ans =

   1.0e+13 *

                   0
   0.000000000001928
   0.000000000052406
   0.000000001551374
   0.000000047660725
   0.000001495105864
   0.000047536735656
   0.001525757556904
   0.049315340974782
   1.602491697370065

可以看出：随着阶数的增加，希尔伯特矩阵的条件数不断增大，矩阵性能变差
11.矩阵的特征值与特征向量

e=eig(A):求矩阵A的全部特征值，构成向量e

[x,d]=eig(A):求矩阵A的全部特征值，构成对角阵d并产生矩阵X，X的每列是相应的特征向量

>> a=[1,1,0;1,0,5;1,10,2]

a =

     1     1     0
     1     0     5
     1    10     2

>> [x,d]=eig(a)

x =

   0.072196186226992   0.975064063761619   0.088619224195265
   0.523368974057523  -0.075013465822402  -0.635606218080313
   0.849042182514069  -0.208861321230112   0.766910274178584


d =

   8.249260679947779                   0                   0
                   0   0.923068166892526                   0
                   0                   0  -6.172328846840312

>> a*x(:,1)

ans =

   0.595565160284515
   4.317407098797336
   7.003970291830360

>> d(1)*x(:,1)

ans =

   0.595565160284514
   4.317407098797333
   7.003970291830354

>> 

12.稀疏矩阵

只储存矩阵的非零元素的值及其位置，即行号和列号，矩阵元素的储存顺序并没有改变，可以大大节约储存空间。

a=sparse(s) : 转化稀疏矩阵

s=full(A) ：转化回完全储存方式

sparse(m , n):生成一个m*n的所有元素为0的稀疏矩阵

sparse(u,v,S): u,v,S是3个等长的向量，s是要建立的稀疏矩阵的非零元素，u(i),v(i)分别是s(i)的行和列下标

>> a=sparse([1,2,2],[2,1,4],[4,5,-7])

a =

   (2,1)        5
   (1,2)        4
   (2,4)       -7

>> b=full(a)

b =

     0     4     0     0
     5     0     0    -7

>> 

让我们通过一个实例来了解一下矩阵的各种应用：
PCA降维法：
设法将原来众多的具有一定相关性的变量，重新组合成一组新的相互无关的综合变量来代替原来的变量。
步骤：1）.对原始数据进行0-1标准化处理
2）.计算样本相关系数矩阵
3）.计算相关系数矩阵的特征值
4）.选择p个主成分，写出主成分表达式
代码如下：

>> A=xlsread('D:\matlabdata\matlabdatas\matLab\Cha3\P3_1_PCA\Coporation_evaluation.xlsx','B2:I16');
>> a=size(A,1);
>> b=size(A,2);
>> for i=1:b
SA(:,i)=(A(:,i)-mean(A(:,i)))/std(A(:,i)); %  A(:,i)A矩阵的第i列
end
>> CM=corrcoef(SA);
>> [V,D]=eig(CM);
>> for j=1:b
DS(j,1)=D(b+1-j,b+1-j);
end
>> for i=1:b
DS(i,2)=DS(i,1)/sum(DS(:,1));
DS(i,3)=sum(DS(1:i,1))/sum(DS(:,1));
end
>> T=0.9;
>> for k=1:b
if DS(k,3)>=T
com_num=k;
break
end
end
for j=1:com_num
PV(:,j)=V(:,b+1-j);
end
>> new_score=SA*PV;
>> for i =1:a
total_score(i,1)=sum(new_score(i,:));
total_score(i,2)=i;
end
>> result_report=[new_score,total_score];
>> redult_report=sortrows(result_report,-4);
>> result_report=sortrows(result_report,-4);

原始表格如下

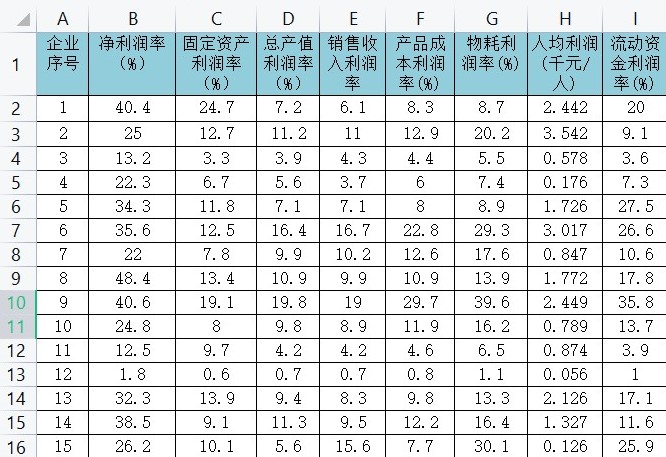
处理结果如下

特征值及其贡献率，累计贡献率：
DS =

    5.7361    0.7170    0.7170
    1.0972    0.1372    0.8542
    0.5896    0.0737    0.9279
    0.2858    0.0357    0.9636
    0.1456    0.0182    0.9818
    0.1369    0.0171    0.9989
    0.0060    0.0007    0.9997
    0.0027    0.0003    1.0000
信息保留率T对应的主成分数与特征向量：
>> com_num

com_num =

     3

>> PV

PV =

    0.3334    0.3788    0.3115
    0.3063    0.5562    0.1871
    0.3900   -0.1148   -0.3182
    0.3780   -0.3508    0.0888
    0.3853   -0.2254   -0.2715
    0.3616   -0.4337    0.0696
    0.3026    0.4147   -0.6189
    0.3596   -0.0031    0.5452
主成分得分及排序（按第4列的总分进行降序排序，前3列为个主成分得分，第5列为企业编号）
result_report =

    5.1936   -0.9793    0.0207    4.2350    9.0000
    0.7662    2.6618    0.5437    3.9717    1.0000
    1.0203    0.9392    0.4081    2.3677    8.0000
    3.3891   -0.6612   -0.7569    1.9710    6.0000
    0.0553    0.9176    0.8255    1.7984    5.0000
    0.3735    0.8378   -0.1081    1.1033   13.0000
    0.4709   -1.5064    1.7882    0.7527   15.0000
    0.3471   -0.0592   -0.1197    0.1682   14.0000
    0.9709    0.4364   -1.6996   -0.2923    2.0000
   -0.3372   -0.6891    0.0188   -1.0075   10.0000
   -0.3262   -0.9407   -0.2569   -1.5238    7.0000
   -2.2020   -0.1181    0.2656   -2.0545    4.0000
   -2.4132    0.2140   -0.3145   -2.5137   11.0000
   -2.8818   -0.4350   -0.3267   -3.6435    3.0000
   -4.4264   -0.6180   -0.2884   -5.3327   12.0000
可以看出，第9家的综合实力最强，第12家的综合实力最弱