Crypto知识
Crypto知识
在逆向中常常会遇到各种加密算法。虽然Reverse中对Crypto的要求不算很高,但了解常见加密方法的基本原理,有助于识别加密算法中的魔改,也能够自己编写exp而不是死板地套用他人的脚本。
BaseX
Base系列编码方法,思想基本一致,就是将密文转换为二进制再分组,将每一组二进制用新的字符代替。
Base16
将二进制分割为4位一组,并将二进制映射为十六进制的16个字符。位数不够4的倍数可以填充0。
Base32
将二进制分割为5位一组,映射为32个字符,不够5的倍数填"="。
映射表为A~Z,2~7
Base58
1.(可选)添加版本前缀,计算校验和。
2.将二进制数据视为一个大整数,使用Base58字符集的字符作为数字的基数。
3.重复地将大整数除以58,记录余数生成字符,直到商为0。
4.反转生成的字符顺序
Base64
最常见。
Base85 91 100
少见。遇到填坑。
识别
找码表。
解码
-
在线网站。Cyberchef支持换表。
-
python脚本。
encode:
# coding=utf-8 import base64 #转换为utf-8 string = 'hello'.encode("utf-8") #encode()不填时默认为utf-8 #baseX编码 base16 = base64.b16encode(string) print(base16)decode:
# coding=utf-8 import base64 string = 'NBSWY3DP' #baseX解码 base32 = base64.b32decode(string) print(base32)常见魔改
换表。有时候会隐藏换表算法,注意寻找。
分组位数或许也会有魔改?目前还没遇到。
RC4
对称加密。
RC4的关键变量
1.密钥流:根据明文和密钥生成密钥流,密钥流长度和明文长度对应,明文长度=密钥流长度=密文长度。因为密文第i字节=明文第i字节xor密钥流第i字节。
2.状态向量S:长度为256,s[0]~s[255]。每个单元都是一个字节。
3.临时向量T:长度为256,每个单元也是一个字节。如果密钥长度为256字节,就直接将密钥的值赋予T,否则循环赋予。
4.密钥K:长度为1-256字节,通常取16字节(其实不怎么通常)。
加密原理(C/C++)
1.初始化S&T
//初始化S和T,S[i]=i,使用密钥对T循环赋值 void initial() { for(int i=0;i<256;++i){ S[i]=i; T[i]=K[i%keylen]; } }2.初始排列S
//对S进行初始化排序 void rangeS() { int j=0; for(int i=0;i<256;++i){ j=(j+S[i]+T[i])%256; swap(S[i],S[j]); } }3.产生密钥流
//根据明文长度和S生成密钥流k len为明文的字节数 void RC4::keyStream(int len) { initial(); rangeS(); int i=0,j=0,t; while(len--){ i=(i+1)%256; j=(j+S[i])%256; swap(S[i],S[j]); t=(S[i]+S[j])%256; k.push_back(S[t]); } }4.将k的每一位与原文进行异或得到密文
for(int i=0;i<lenFile;++i){ out<<(unsigned char)(bits[i]^k[i]);解密
通过对加密算法的分析我们得知:只要知道明文长度和密钥,就能够确定密钥流,而且加密方法又是可逆性很好的异或算法。因此解密的思路比较明确:
1.获得密钥流
2.将密文与密钥流每一位进行异或
魔改
RC4的魔改无非在生成密钥流的过程中进行,比如对key偷偷操作一下,改一改操作轮数之类的。但我们生成密钥流的办法其实就是完全照搬原来的算法,所以这个过程中魔改了什么其实不是很重要,主要是要看出来并在exp中体现。
题外话
在看相关exp中注意到一些小tips记录一下。
1.不引入新变量tmp实现swap(可能会遇到~~(其实OI竞赛里学过但早忘了我是RJ,5555)~)
a=a+b; b=a-b;//b=a(ori) a=a-b;//a=b(ori)2.unsinged char与char
参考:(https://blog.csdn.net/huangyimo/article/details/82980364)
“程序实现时,需要注意的是,状态向量数组S和临时向量数组T的类型应设为unsigned char,而不是char。因为在一些机器下,将char默认做为signed char看待,在算法中计算下标i,j的时候,会涉及char转int,如果是signed的char,那么将char的8位拷贝到int的低8位后,还会根据char的符号位,在int的高位补0或1。由于密钥是随机产生的,如果遇到密钥的某个字节的高位为1的话,那么计算得到的数组下标为负数,就会越界。”
总结:涉及到char转int问题时,最好使用unsigned char而非char。
RSA
基于大数分解难题的加密算法,非对称。
相关数论知识
同余
给定整数a,b,若有正整数m,(a-b)%m==0,则称a,b对于模m同余,记作a≡b(mod m)。
其意义是a,b对m取模结果相等。
乘法逆元
如果ax≡1(mod m),且gcd(a,m)=1,则称a关于模m的乘法逆元为x。
只有a,m互质时,a才有关于p的逆元。
若将a关于模p的逆元记作inv(a),则有应用:(a/b)%p≡(a*inv(b))%p
例子:当a=3,m=5,那么a关于模5的逆元为2,因为有:
3*2≡1(mod 5)
费马小定理Fermat's little theorem是求解逆元的一个重要方法:
如果p是一个质数,而a不是p的倍数,则有ap-1 ≡ 1 (mod p)
所以当p为质数的时候,ap-2 就是a关于模p的逆元
扩展欧几里得算法Extended euclidean algorithm也可求解逆元。
欧拉函数
OI学过euler筛法筛质数。
φ(n)表示小于等于n的正整数中与n互质的数的数目。
密钥生成步骤
1.找两个大素数p,q
2.n=pq
3.Euler Formula: φ(n)=(p-1)(q-1)
4.选定e,使得1<e<φ(n),且e与φ(n)互质。
5.计算e关于φ(n)的模逆元d。
得到公钥pk=(e,n),私钥sk(d,n)
加解密步骤
给定明文M,加密过程如下:
- 计算C≡Me (mod n),得到的C就是密文。
给定密文C,解密过程如下:
- 计算M≡Cd (mod n),得到的M就是解密后的明文。
例题
来自buuctf reverse rsa
压缩包里有flag.enc(密文),pub.key(密钥)
把密钥扔进在线网站解析可以得到e,n
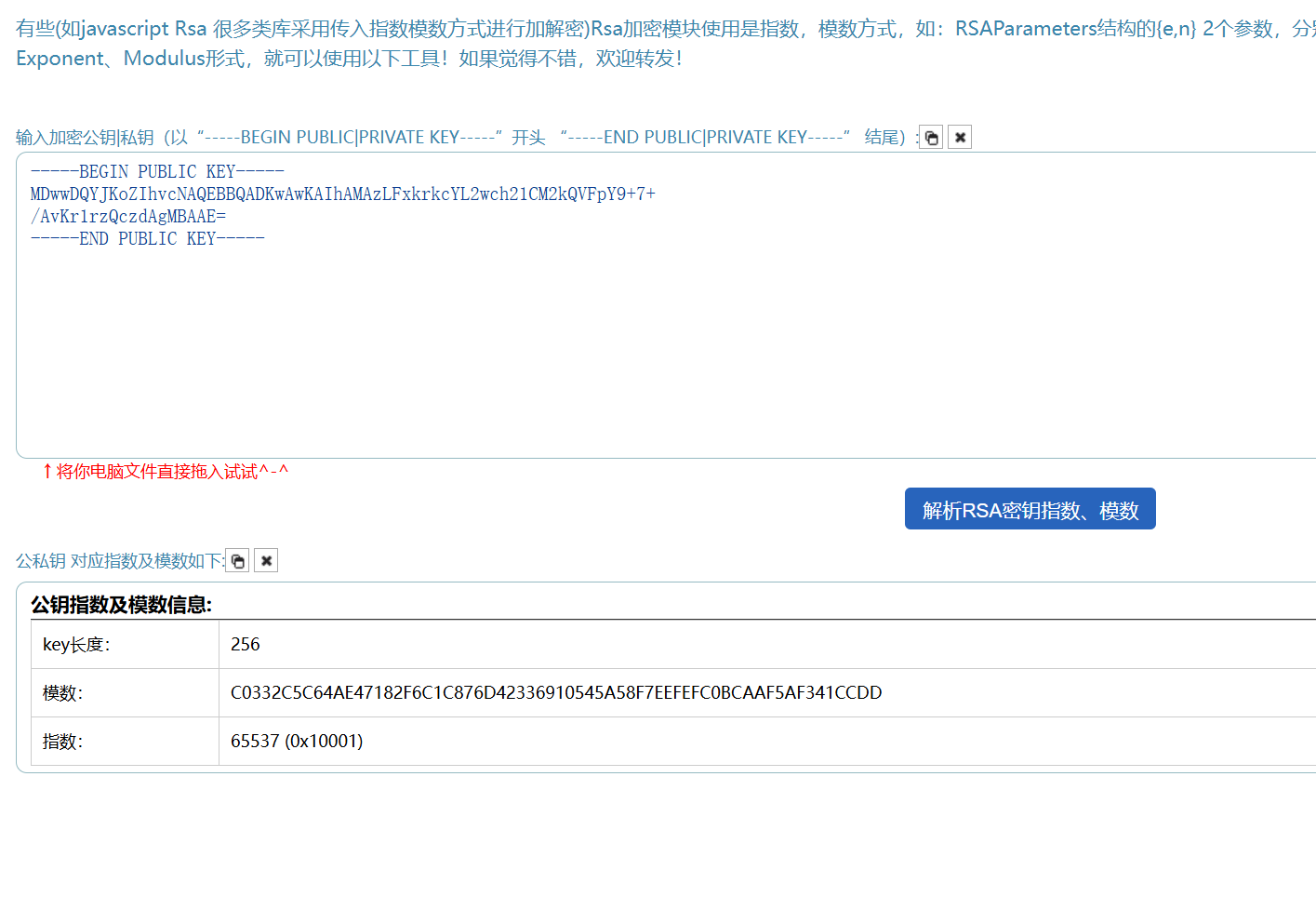
在线大数分解n可以得到:
p=285960468890451637935629440372639283459
q=304008741604601924494328155975272418463然后可以计算φ(n),d,获得私钥key,随后利用python的rsa库进行解密,打开flag.enc作为密文。
import gmpy2 import rsa e=65537 p=285960468890451637935629440372639283459 q=304008741604601924494328155975272418463 n=p*q eul=(p-1)*(q-1) d=gmpy2.invert(e,eul) key = rsa.PrivateKey(n, e, int(d), p, q) with open("C:\\Users\\accel\\Desktop\\output\\flag.enc","rb+") as f: f=f.read() print(rsa.decrypt(f,key)) #b'flag{decrypt_256}\n'End
还有美好的TEA大家族,AES等,特别是TEA,得额外再写一篇。
贴一张5.5周年荒芜拉普兰德大头照(物理意义上的大头)。






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
· 【杂谈】分布式事务——高大上的无用知识?