前两天去听了一下搞代数几何的Dino Lorenzini在交大的两场讲座(“On Laplacian Of Graphs and Generalization”,“Riemann-Roch Theorem for graphs and generalizations”),在此将笔记整理一下。$\newcommand \diag{\mathrm{diag}} \newcommand\Z{\mathbb{Z}} \newcommand\Pic{\mathrm{Pic}} \newcommand\img{\mathrm{Im}} \newcommand\di{\mathrm{div}}$
首先定义一些记号:$G$是一个连通无向图,有$n$个顶点(记为$v_1,v_2,\cdots,v_n$),$m$条边,且无自循环。$A$为$G$的领接矩阵,即为$(a_{ij})$,其中$a_{ij}$为$v_i$与$v_j$($i\not= j$)之间边的个数,$a_{ii}=0$。图的Laplacian是$D-A$,其中$D$是对角阵,$\mathrm{diag}(d_1,d_2,\cdots,d_n)$,其中$d_i$为$a_i$的度,即连接到$v_i$的边的个数。
1.图的Laplacian以及Smith标准型
对于一个图的Laplacian来说,在代数图论中研究的大多是它的特征值。而在矩阵理论中,除了特征值以外还有其他一些不变量,比如说Smith标准型。
定义1 (Smith标准型) 整系数矩阵$M$的Smith标准型是$\mathrm{SNF}=\mathrm{diag}(\delta_1,\delta_2\cdots,\delta_n)$,其中$\delta_1\cdots\delta_i=\Delta_i$,其中$\Delta_i$是$M$的所有$i$阶子式的最大公因数。
注意到它同样有一个等价定义,也就是说,$m\times n$阶矩阵$M$的Smith标准型是$SMT$,其中$S,T$分别为$m\times m$以及$n\times n$阶的矩阵。使得$SMT$为对角阵$\mathrm{diag}(\delta_1,\delta_2\cdots,\delta_n)$,使得$\delta_1|\delta_2|\cdots |\delta_n$,其中$\delta_i\in\mathbb{Z}$。同样我们可以注意到,当$\det{M}=0$的时候,$\delta_n=0$。
我们知道,对于Laplacian矩阵$M$的特征值$\lambda_1,\cdots,\lambda_n$,可以使$\lambda_1\ge\lambda_2\ge\cdots\ge\lambda_n=0$。而图的生成树的个数不是别的,就是\[\#(\mbox{生成树})=\frac{1}{n}\lambda_1\cdots\lambda_{n-1}.\]这是代数图论中经典的Kirchhoff定理。通过Smith标准型的第一个定义,我们同样可以容易知道\[\#(\mbox{生成树})=\delta_1\cdots\delta_{n-1}.\](通过对Kirchhoff定理的证明可以看出,图的生成树个数正是Laplacian的任意一个$n-1$阶子式的行列式绝对值)
Smith标准型与特征值的联系不仅限于此,如果我们定义$\mu$为相异特征值的乘积,那么如下定理成立
定理2 (Smith标准型与特征值联系)
- $\mu\in\mathbb{Z}$
- $n|\mu$
- $\delta_{n-1}|\mu$,但是一般来说,$\delta_{n-1}\nmid \frac{\mu}{n}$
定理的证明可见Lorenzini的文章。
2.算术图(Arithmetical graph)以及Picard群
每一个图,我们都有一个Laplacian矩阵$M$。而我们又知道,$M(1,1,\cdots,1)'=0$,所以我们可否将Laplacian的概念推广呢?这样就引出了“算术图”的想法。
定义3 (算术图) 算术图是三元组$(G,M,R)$使得以下成立:
- $G$为图
- $M=C-A$,其中$A$为领接矩阵,$C$为系数为正整数的对角阵,记为$\mathrm{diag}(c_1,c_2,\cdots,c_n)$。
- $R=(r_1,r_2,\cdots,r_n)'$,其中$r_i>0$,且同有$r_i\in\mathbb{Z}$,且$\gcd{(r_1,\cdots,r_n)}=1$。
- $MR=0$
一个简单的例子是Extended Dynkin Diagram赋予如下数字:
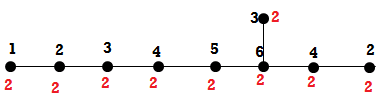
其中黑色数字代表了向量$R$赋予的值,而红色的数字则是对角阵$M$赋予的值,通过计算很容易可以验证$MR=0$如下

有了算术图的定义,我们可以定义它的不变量,即Picard群。这个群来源于代数几何的想法。
定义4 (Picard群)整数群$\mathbb{Z}$模去$M$的像$\mathbb{Z}^n/\mathrm{Im}(M)$称为算术图的Picard群,记为$\mathrm{Pic}(G)$。同时我们定义degree map为$\deg:\mathbb{Z}^n/\mathrm{Im}(M)\to \mathbb{Z}$,使得$(s_1,s_2,\cdots,s_n)\mapsto\sum_{i=1}^n r_i s_i$,其中$r_i$即为算术图中$R$的元素。
有了这一定义,我们就可以得到有限阿贝尔群$\Phi_M=\ker(\deg)$。可以证明,如果$\diag(\delta_1,\delta_2,\cdots,\delta_{n-1},0)$为Smith标准型,就有\[\Phi_M\cong \mathbb{Z}/\delta_1\mathbb{Z} \times \mathbb{Z}/\delta_2\mathbb{Z}\times\cdots\times \mathbb{Z}/\delta_{n-1}\mathbb{Z}.\]
注记:由此可以看出$\Phi_M$是循环群当且仅当$\mathrm{SNF}=\diag(1,\cdots,1,\delta_{n-1},0)$。
于是特别地,考虑$M$为$G$的Laplacian,如果$G$的生成树的个数无平方因子,自然就有$\Phi_M$是循环群。而$\Phi_M$是循环群的$G$占了很大比例。以下是两个结论:
- Chen-Ye(2008) 给定图$G$,存在同构的图$G'$,由$G$的细分(至多$m-n$条边)给出,且$\Phi_{M'}$是循环群。
- Wood(2014) 对于$n$点的Erdos-Renyi随机图,当$n\to\infty$时,
(a) $|\Phi_M|$无平方因子的概率约为$48.2\%$
(b)$\Phi_M$是循环群的概率约为$79.3\%$
3.算术图的不变量
(1)第一贝蒂数:$\beta(G)=m-n+1$,相当于图中不相关的“圈”的个数,就是将所有的边个数减去生成树的长度即为不相关圈的个数。
(2)亏格: $g_0(G,M,R)$,定义为\[2g_0(G)-2=\sum_{i=1}^n r_i(d_i-2).\]注意到这样一个亏格和我们通常所说的图的亏格(可嵌入多少亏格的曲面使得边不相交)不一样。因为$K_{3,3}$和$K_5$都有图亏格$1$,但是简单计算就可发现$g_0(K_{3,3})=4$,$g_0(K_5)=6$。
简单计算可以发现,\[2g_0(G)-2\beta(G)=\sum_{i=1}^n(r_i-1)(d_i-1).\]故而有如下定理。图的亏格的几何意义可见下定理链接中的引文[7]与[8]。
定理5(Lorenzini,1989)
- $g_0(G)$为整数
- $g_0(G)\ge \beta(G)\ge 0$
(3)$g$-数: $g$-数的定义如下。我们知道$\deg:\Pic(G)=\Z^n/\img(M)\to \Z$将$\Phi_M$映射至$0$,那么$g$-数是最小的整数,满足
- 对于任意$\deg[D]\ge g$的代表元$[D]\in\Pic(G)$,存在$V\in \img(M)$使得$D+V$在第一卦限(也即$D+V$的各个坐标都大于$0$)
- 存在$\deg[D]=g-1$使得$\forall V\in\img(M)$,都有$D+V$不可能在第一卦限。
这样的$g$存在吗?存在性已经被证明,而以下的标志性的定理找出了一般图的解:
定理6(Baker & Norine, 2006)
若$G$为一般的图,且$R=(1,1\cdots,1)'$,那么$g=\beta(G)$。
而这一定理同样也关乎图的黎曼-罗赫结构。两人首次提出了图上的黎曼-罗赫结构,而Lorenzini则进一步提出了如下定理:
定理7(Lorenzini,2011)如果$g(G)=g_0(G)$,那么图上就有黎曼-罗赫结构。
黎曼-罗赫结构将在下一节提到。这节最后再给出一些对不变量关系的估计。
定理8 令$(G,M,R)$为算术树(也即算术图中的$G$为树),那么
- $|\Phi_M|=\prod_{i=1}^n r_i^{d_i-2} \in \mathbb{N}$
- $|\Phi_M|\le 4^{g_0(G)}$
- 若$p$为整除$|\Phi_G|$的素数,那么$p\le 2g_0(G)+1$
通过第二个等式,且我们知道$g\le g_0$,那么是否有$|\Phi_M|\le 4^g$呢?现在还不得而知。对于$\Phi_G$这个群生成元的估计。在普通的图$G$中,$\Phi_G$可以被$\beta(G)$个元素生成。而对于一般的算术图的结果如下:
定理9 令$(G,M,R)$为无重边的算术图,且假定对于某个$i$有$r_i=1$。那么\[\mathrm{SNF}(M)=\diag(\delta_1,\cdots,\delta_{n-1-\beta},\delta_{n-\beta},\cdots,\delta_{n-1},0)\]其中$\Delta_{n-1-\beta}=\delta_1\cdots\delta_{n-1-\beta}$有$\Delta_{n-1-\beta}|\prod_{i=1}^n r_i^{d_i-2}$
4.图上的黎曼-罗赫定理与双变量Zeta函数(Two-variable zeta function)
动机是来自于代数几何的黎曼罗赫定理。$X$是$\mathbb{C}$上的射影曲线(即$\mathbb{C}P^2$中齐次函数$F(x,y,z)$的解)。$f$是定义在射影曲线上的亚纯函数,且有有限个零点与极点。那么定义$f$的$\di$为 \[\di(f)=\sum_{P\in X}m(P) P\],其中$m(P)$为重数。在$m(P)>0$为零点,$m(P)<0$为极点。而一个重要的结论是,零点与极点的个数相同!也即$\sum_P m(P)=0$。
而类似地,我们可以定义“除子”(Divisor)$D$为$D=\sum_P a_P P$,是为关于$P$的形式和,其中$a_P\in\Z$且为有限和。定义度函数\[\deg(D)=\sum_P a_P.\]从定义可以看出$\deg\circ \di=0$。同时对于任意的除子$D$,我们可以赋予它另外一个整数$h^0(D)$,定义为\[h^0(D)=\dim_{\mathbb{C}} H^0(X,\mathcal{O}_D),\mathcal{O}_D=\{f|f\mbox{只在}a_P\not=0\mbox{的地方有极点,且}m(P)\ge-a_P\}\]是为$\mathcal{O}_D$层的上同调群的维数。
对于这样的结构,定义$[D]$为$D$的等价类,即为$\{D'|\exists f,D'=D+\di(f)\}$。那么就有经典的黎曼-罗赫定理(Riemann-Roch)如下
定理10(黎曼-罗赫)存在典范类(Canonical class)$[K]$使得对于任意$D$都有\[h^0(D)=\deg(D)+1-g+h^0(K-D)\]
而在代数几何中,$[D]$的类构成了维数$g$的代数簇上的所有点,称为Picard簇$\Pic(X)$。而$[D]$满足$\deg(D)=0$的子类被称为曲线$X$的Jacobian。
对应的图论中来,注意到前面我们其实已经提到了和代数几何这些结果相仿的定义,比如Picard群,$\Phi_M$等等。前面一直没有说明的$\Phi_M$有了它的名字,称为雅可比簇(Jacobian Variety),它的阶记为$G$的生成树的个数。而典范类$[K]$定义为$[(d_1-2,\cdots,d_n-2)]$。
Baker与Norine首次给出了图上的黎曼-罗赫定理。他们赋予每个除子$D$(或者说Picard群的元素)的$h^0(D)$,且证明了图上的黎曼-罗赫定理\[h^0(D)=\deg(D)+1-\beta(G)+h^0(K-D)\]对于$h^0(D)$的定义将在之后提到。
如果我们有了$h^0:\Pic(G)\to \Z$,那么我们就可以定义一个zeta函数\[Z_h(G,u,t)=\sum_{[D]\in\Pic(G)}\frac{u^{h^0(D)}-1}{u-1}t^{\deg(D)}.\]而一个稍微变化的定义是\[W_h(G,x,y)=\sum_{[D]\in\Pic(G)}x^{h^0(G)}y^{h^0(K-D)}.\]这个zeta函数的定理动机来自与有限域上的曲线上的zeta函数:令$p$为素数$\Z/p\Z=\mathbb{F}_p\le \mathbb{F}_{p^s}$。令$X/\mathbb{F}_p$为光滑射影曲线(比如$\mathbb{P}^2$上的齐次$F(x,y,z)=0$),那么令$a_s$为在系数为$\mathbb{F}_{p^s}$中时,曲线方程解的个数。那么有限域中与黎曼zeta相对应的zeta函数为:\[Z(X/\mathbb{F}_p,T)=\exp\left(\sum_{s=1}^\infty a_s\frac{T^s}s \right)=\sum_{[D]\in\Pic(X)}\frac{p^{h(D)}-1}{p-1}T^{\deg(D)}\]与我们这里的zeta函数类似。这样的zeta函数同样又给出了图的一个不变量。
最后给出$h^0(D)$的定义以及一些性质(等价意思是相差一个$\img(M)$的元素):
定义11($h^0(D)$)定义$E\in \Z^n$是“有效的”当$E\ge 0$,也就是$E$的每个坐标都大于等于$0$。如果$\deg(D)<0$,则令$h^0(D)=0$。如果$\deg(D)\ge 0$,定义$h^0(D)$为\[h^0(D)=\min\{\deg(E)|E\ge 0\mbox{且}D-E\mbox{不等价于一个有效的元素}\}\]
注意到这儿的定义其实类似前面我们所说的$g-$数。不过$g-$数相当于一个全局的不变量。于是我们有如下的性质:
- $h^0(D)\ge 0$这个通过定义显然
- 若$D$不等价与一个有效的元素,那么$h^0(D)=0$,由于定义中集合包含了$E=0$。
- $h^0(D)\le \deg(D)+1$,更进一步,只可能在如下图的区域内有点

我曾经问在$\deg(D)$不变的时候是否能够变量区域中竖线交的所有点,不过还没有开始计算。
- 若$\deg(D)\ge 2\beta(G)-1$,那么$h^0(D)=\deg(D)+1-\beta(G)$
对于不变量zeta函数,我们同样也有一些比较好的性质,定理的证明都可以在[3]中找到。
定理12
- 有理性,\[Z_h(G,u,t)=\frac{f(u,t)}{(1-t)(1-ut)},\]其中$f(u,t)\in\Z[u,t]$,有形式\[f(u,t)=1+c_1(u)t+c_2(u)t^2+\cdots+c_g(u)t^g+uc_{g-1}(u)t^{g+1}+u^2 c_{g-2}(u)t^{g+2}+u^g t^{2g}.\]
- $f(u,t)$在$\mathbb{C}[u,t]$中不可约。
- $f(1,u)=\#G\mbox{的生成树}$。
- \[Z\left(u,\frac{1}{ut}\right)=(ut^2)^{1-g}Z(u,t)\]
- 若$G$为树,则$Z(G,u,t)=\frac{1}{(1-t)(1-ut)}$
最后值得注意的一点是,zeta函数,Tutte多项式,Smith标准型,特征值这些不变量似乎是相互无关的!可见Julian Clancy、Timothy Leake与Sam Payne最近的文章。
PS:对于计算$h^0$,Baker博客给出过一个链接,可供参考
拓展阅读(定理的证明大多来自这几篇):
[1]"Arithmetical Graph" by Dino Lorenzini,1989
[2]"Riemann-Roch Theorem and Abel-Jacobi theory on a finite graph" by Matthew Baker, Serguei Norine,2006
[3]"Two variable Zeta-functions on graphs and Riemann-Roch Theorems"by Dino Lorenzini,2011




