我们所用的是C.L.Evans "Partial Differential Equations"
$\def\dashint{\mathop{\mathchoice{\,\rlap{-}\!\!\int}
{\rlap{\raise.15em{\scriptstyle -}}\kern-.2em\int}
{\rlap{\raise.09em{\scriptscriptstyle -}}\!\int}
{\rlap{-}\!\int}}\nolimits}$
$\newcommand\argmin{\operatorname{arg\,min}}$
$\newcommand\esssup{\operatorname{ess\,sup}}$
$\newcommand\supp{\operatorname{supp}}$
1.Prelimary
1.1 Variational method
For a partial differential equation(for instance, the Poisson equation):
$$
\left\{ \begin{array}{rl}
-\Delta u(x) & = f(x) \quad\mbox{ if $x\in B\subseteq\mathbb{R}$}
\\ u(x)|_{\partial B} & = 0
\end{array} \right.
$$
We may define the operator that values the "Energy" of the function
Definition 1.Energy Operator $J(u)$ is defined as
$$J(u)=\int_{B}\left(\frac{1}{2}|\nabla u|^2+f(x)u(x)\right)dx$$
We may be interested in the minimum of the operator,
$$\bar{u}=\underset{u\in\mathcal{H}_{0}^{1}(B)}{\argmin}J(u)$$
By this definition, we may have the following theorem:
Theorem 1.(Existence of Weak Solution) $\bar{u}$ exists, and is the weak solution of the Poisson equation.
Proof: First part: existence of certain $\bar{u}$
-
First, note that
\[J(u)\ge \frac{1}{2}\int_{B}|\nabla u|^2-\epsilon\int_{B}u^2-\frac{1}{4\epsilon}\int_{B}f^2\]
This is done by AM-GM. By Poincaré Inequality, we know that
\[J(u)\ge \left(\frac{1}{2}-\epsilon C\right)\|u\|^2-\frac{1}{4\epsilon}\int_{B}f^2\]
which states that $J(u)$ has a finite infimum. -
Second, we may show that if $J(u_n) \searrow m$,where $m$ is the infimum. Then $u_n$ has a subsequence that converge to $\bar{u}$. That is, the uniform bound on $J(u_n)$ results in the uniform bound of $\|u\|^2$. This is obtained by Cauchy-Schwarz Inequality and Poincaré inequality,
\[J(u)\ge \frac{1}{2}\| u \|^2-\| f\|_{L^2}\| u \|_{L^2}\ge \frac{1}{2}\left(\| u \| -C \| f \|_{L^2}\right)^2-\frac{1}{2}C^2 \| f\|_{L^2}\]
That is to say, $\| u_n \|\le C\|f\|_{L^2}$ - By weak compactness, we know that there is a weak converging sequence $u_{n_k}\to \bar{u}$, $\|\bar{u}\| \le \underline{\lim}\|u_n\|$
-
The convexity functional $J(u)$ guarantee that
\[m=\lim_{n}J(u_n)=\lim_{n\to\infty}\frac{1}{2}\|u_n\|^2+\lim\int f u_n\ge \frac{1}{2}\|\bar{u}\|^2+\int f\bar{u}=J(\bar{u})\]
Second part: We derive that $\bar{u}$ is the weak solution .
Let $h(0)=J(\bar{u})\le J(\bar{u}+tv)=h(t)$ fot $t\in\mathbb{R}$. Where $v\in \mathcal{H}_{0}^{1}(B)$. This means $h'(0)=0$.
Since
\[h(t)=\frac{1}{2}\int |\nabla \bar{u}|^2+t\int \nabla \bar{u}\nabla v+\frac{1}{2}t^2\int|\nabla v|^2+\int f\bar{u} +t\int fv\]
The derivative at 0 is given by
\[0=\int \nabla \bar{u}\nabla v+\int fv\]
Also, by Green's formula
\[\int_{B}\nabla \bar{u}\nabla v=\int_{\partial B}v\frac{\partial \bar{u}}{\partial n}-\int_B v\Delta \bar{u}=-\int v\Delta u\]
Combining these two equations we get
\[\int_B (-\Delta \bar{u}+f)vdx\equiv 0 \textrm{ holds for all }v\in\mathcal{H}_{0}^{1}(B)\]
And done.$\square$
This proof also gives a sufficient and necessary condition for $\bar{u}$ to be the weak solution of the Poisson equation, that is
\[\int \nabla \bar{u}\nabla v+\int fv\equiv 0\quad \forall v\in\mathcal{H}_{0}^{1}(B)\]
The same method also provides us the truth that $J'(\bar{u})=0$. But the derivative of an operator remains to be defined, which will be mentioned in the generalized function section below.
1.2 Tools From ODE
Consider the ordinary differential equation:
\begin{equation*}
\begin{cases}
u'(t)=f(u(t),t)\\
u(0)=u_0
\end{cases}
\end{equation*}
where $f$ is continuous on $(u_0-1,u_0+1)\times(-\infty,+\infty)$, and Lipschitz in $u$. We want to prove the existence and uniqueness of the function. The easy proof is given by the recursion.
- First we define $T:X\to X$ be the operator:
\[T(\varphi)(t)=u_0+\int_{0}^{t}f(\varphi(s),s)ds\]
It's easy to check that $T(\varphi)(0)=0$, and $\exists t$ such that $|T(\varphi)(t)-u_0|\le \frac{1}{2}$( this can be done by Lipschitz condition). -
We may prove the contraction of the operator.
\begin{align*}\|T(\varphi_1)(t)-T(\varphi_2)(t)\|&\le\int_{0}^{t}\left|f(\varphi_1(s),s)-f(\varphi_2(s),s)\right|ds\\
&\le M\int_{0}^{t}\|\varphi_1-\varphi_2\|_{L^{\infty}}ds\le M\delta\|\varphi_1-\varphi_2\|_{L^{\infty}}\\
&\le \frac{1}{2}\|\varphi_1-\varphi_2\|_{L^{\infty}}
\end{align*}
This holds for $M\delta\le \frac{1}{2}$, $\delta=\min\{\frac{1}{2M},1\}$. This means $T$ is a contraction map(Since $M$ does not change, so $\delta$ does not change). -
(Homework 1)In this section, we prove that $T$ has a unique fixed point.
$\forall \varphi^{(0)}\in X$, we denote $\varphi^{(n)}=\overbrace{T\circ T\circ \cdots \circ T}^{n\textrm{ times}}(\varphi^{(0)})$.
So for all $n\in\mathbb{N}$,
\[\|\varphi^{(n)}(t)-\varphi^{(0)}(t)\|_{L^{\infty}}\le\sum_{k=1}^{n}\|\varphi^{(k)}(t)-\varphi^{(k-1)}(t)\|_{L^{\infty}}\le 2\|\varphi^{(1)}(t)-\varphi^{(0)}(t)\|\le 2P\]
where $P $ is a number greater than left hand side.So $\forall \epsilon>0,\exists N\in\mathbb{N},\frac{1}{2^{N-1}}\le\epsilon$, $\forall m>n>N$, we have
\[\|\varphi^{(m)}(t)-\varphi^{(n)}(t)\|_{L^{\infty}}\le \frac{1}{2^{n}}\|\varphi^{(m-n)}(t)-\varphi^{(0)}(t)\|_{L^{\infty}}\le \epsilon\]
By the completeness of $L^{\infty}$ we know that $\varphi^{(n)}$ is a Cauchy sequence and converge to a point $\varphi$. And since \[\lim_{n\to\infty}\|\varphi^{(n)}(t)-\varphi^{(n-1)}(t)\|_{L^{\infty}}=0\] we know that $T(\varphi)=\varphi$.To show the uniqueness, if $T(\psi)=\psi$, we have
\[0\le\|\psi-\phi\|_{L^{\infty}}=\|T(\varphi)-T(\psi)\|_{L^{\infty}}\le\frac{1}{2}\|\psi-\phi\|_{L^{\infty}}\]
which means $\phi\equiv \psi$. and the proof is done.
To show the tools from the ODE, we consider the Heat equation
$$
\left\{ \begin{array}{rl}
u_t & = \Delta u \quad\mbox{ in $\mathbb{R}$}
\\ u(x,0) & = u_0(x)
\end{array} \right.
$$
By the analysis in PDE course, we derive that
\[u(x,t)=e^{\Delta t}u_0=\int_{\mathbb{R}^n}H(x-y,t)u_0(y)dy\]
where $H(x,t)$ denotes the heat kernel, with representation
\[H(x,t)=\frac{1}{(4\pi t)^{d/2}}e^{-|x-y|^2/4t}\]
However, when handling this kind of problem
$$
\left\{ \begin{array}{rl}
u_t & = \Delta u +f(u,x,t)
\\ u(x,0) & = u_0(x)
\end{array} \right.
$$
The addition of non-linear term makes it hard to analysis, so we use the similar method in ODE, that is omitting the space term and get
\[u'=Au+f(u,t)\Rightarrow u(t)=e^{At}u(0)+\int_{0}^{t}e^{A(t-\tau)}f(u_0(\tau),\tau)d\tau\]
where $A$ denotes an operator, and the first term can be analyzed by the heat equation before,
\begin{align*}u(x,t)&=e^{\Delta t}u_0+\int_{0}^{t}e^{\Delta(t-\tau)}f(u(x,\tau),x,\tau)d\tau
\\&=\int_{\mathbb{R}^n}H(x-y,t)u_0(y)dy+\int_{0}^{t}\int_{\mathbb{R}^n}H(x-y,t-\tau)f(u(y,\tau),y,\tau)dyd\tau
\end{align*}
2.Generalized function
2.1 The generalized function
The generalized functions, sometimes called the distributions, are functions generalized to make some functions that with physical means(such as locally integrable) differentiable. The derivatives are generalized so as to meet the use of much physical applications.
The generalization should be done with some principles in hand, such as the Fundamental Theorem of Calculus should also holds in the generalized function space, the functions that is originally differentiable will also be differentiable, and the derivatives should be the same.
To generalize, we use interaction with functions. Instead of observing the function itself, we use some "test functions" to interact with the original one to see the property. The fundamental interaction is the inner product in $L^2$ space, that is
\[\langle f,g\rangle=\int_{\mathbb{R}^n}f(x)g(x)dx\]
where $f$ is locally integrable and $g$ is infinitely differentiable on a compact support set $C_{0}^{\infty}(\mathbb{R}^n)=D$
We define the generalized function as follows: $f:C_{0}^{\infty}(\mathbb{R})\to \mathbb{R}(\mathbb{C})$ that satisfies
- Linearity, $f(a g_1+bg_2)=af(g_1)+bf(g_2)$.
- Continuity, $f(g_n)\to f(g)$ if $g_n\to g$, here $g_n\to g$ is defined as (a)$D^{\alpha}g_n\to D^{\alpha}g$ uniformly and (b)$\exists K\subset\subset \mathbb{R}^n$ such that $g_n(x)=0$ if $x\not\in K$
We denote $D'$ as the space of generalized function.
(Homework 2)Show that locally integrable functions are generalized functions. That is $f\in L_{loc}^{1}(\mathbb{R}^n)\Rightarrow f\in D'$
Proof:
We have $f\in L_{loc}^{1}(\mathbb{R}^n)$ and $\varphi\in C_{0}^{\infty}(\mathbb{R}^n)$, we define operator
\[T_{f}(\varphi):=\int_{\mathbb{R}^n}f(x)\varphi(x)dx\]
This is clearly linear.
The only thing we needs to show is that $\varphi_n\to\varphi$ implies $T_{f}(\varphi_n)\to T_{f}(\varphi)$
\begin{align*}
|T_f(\varphi)|&=\left|\int_{\mathbb{R}^n}f(x)\varphi(x)dx\right|\le\int_{\mathbb{R}^n}|f(x)||\varphi(x)|dx\\
&=\int_{K}|f(x)||\varphi(x)|dx \le\|\varphi\|_{L^{\infty}}\int_{K}|f(x)|dx
\end{align*}
where $K$ is the support of $\varphi$. This holds for all $\varphi$, so we substitute $\varphi_n-\varphi$ into it and gets
\[|T_f(\varphi_n)-T_{f}(\varphi)|\le\|\varphi_n-\varphi\|_{L^{\infty}}\int_{K}|f(x)|dx \]
By definition we know that it converges to zero, that is $T_f \in D'$$\square$
(Homework 3) Define $D^{\alpha}$ in $D'$ so that it is consistent with the definition in classical function spaces.
Proof:By \[D^{\alpha}f(\varphi)=\int_{\mathbb{R}^n}D^{\alpha}f(x)\varphi(x)dx=(-1)^{|\alpha|}\int_{\mathbb{R}^n}f(x)D^{\alpha}\varphi(x)dx\]
this is consistent with all $\varphi\in C_{0}^{\infty}(\mathbb{R}^n)$ by integration by parts. Thus we define
\[D^{\alpha}f(\varphi):=(-1)^{|\alpha|}\int_{\mathbb{R}^n}f(x)D^{\alpha}\varphi(x)dx\]
(Homework 4)Prove that $D^{\alpha} f\in D'$ if $f\in D'$
Proof:Clearly,
\[D^{\alpha} f(a\varphi_1+b\varphi_2)=(-1)^{|\alpha|}\int_{\mathbb{R}^n}f(x)D^{\alpha}(a\varphi_1+b\varphi_2)dx=aD^{\alpha}f(\varphi_1)+bD^{\alpha}f(\varphi_2)\]
the linearity is obvious.
Also by \[|D^{\alpha}f(\varphi-\varphi_n)|=\left|\int_{\mathbb{R}^n}f(x)D^{\alpha}(\varphi-\varphi_n)\right|\]
and $D^{\alpha}\varphi\to D^{\alpha}\varphi_n$ uniformly, that is $\sup_{x\in K}|\varphi-\varphi_n|\to 0$
This means \[D^{\alpha}f(\varphi-\varphi_n)|\le\sup_{x\in K}|\varphi-\varphi_n|\left|\int_{K}fdx\right|\to0\]
this shows that $D^{\alpha}f\in D'\square$
Here we will show two examples of special generalized function.
(Homework 5(a))Let $h(x)$ be that $$
h(x)=\left\{ \begin{array}{rl}
0 \quad (x\le 0)\\
1 \quad (x>0)
\end{array} \right.
$$ Show that $Dh(x)=\delta$.
Proof:$\forall\varphi\in C_{0}^{\infty}(\mathbb{R}^n)$, we have
\[Dh(\varphi(x))=-\int_{\mathbb{R}}h(x)\varphi(x)dx=-\int_{0}^{+\infty}\varphi'(x)=\varphi(0)\]
This means $h'(x)\equiv \delta(x)$ and done.$\square$
(Homework 5(a))Let \[\Gamma(x)=\frac{1}{(n-2)|S^{n-1}||x|^{n-2}}.\quad(n\ge 3,n\in \mathbb{Z})\]
$|S|^{n-1}$ is the surface area of unit sphere with dimension $n$. Show that $$-\Delta \Gamma(x)=\delta_0$$
Proof:Let $B_R$ be the sphere with radius $R$ centered at the origin, we get
\[\int_{B_R}\Delta \Gamma\varphi dx=\int_{B_R\backslash B_{\varepsilon}}\Delta \Gamma\varphi dx+\int_{B_{\varepsilon}} \Delta\Gamma\varphi dx\]
When $x\not = 0$, we have
\[\Delta\Gamma(x)=\sum_{i=1}^{n}\frac{\partial^2}{\partial x_i^2}\Gamma(x)=-C\cdot\sum_{i=1}^{n}\frac{(n-2)(\sum_{k\not = i}x_k^2-(n-1)x_i^2)}{(\sum_{i=1}^{n}x_{i}^2)^{n-2}}\equiv0\]
This means the integration does not depends on the radius:
\[\int_{B_{R}}\Delta\Gamma\varphi dx=\int_{B_{\varepsilon}}\Delta\Gamma\varphi dx\]
By Green's formula
\begin{align*}\int_{B_{\varepsilon}}\Delta\Gamma\varphi dx &=-\int_{B_{\varepsilon}}\nabla\Gamma\cdot\nabla\varphi dx+\int_{\partial B_{\varepsilon}}\nabla\Gamma\cdot \vec{n}\varphi d\sigma \\
&=\int_{B_{\varepsilon}}\Gamma\Delta\varphi dx+\int_{\partial B_{\varepsilon}}(\nabla\Gamma\cdot \vec{n}\varphi-\Gamma\nabla\varphi\cdot \vec{n})d\sigma
\end{align*}
Since $\Delta\varphi$ and $\nabla\varphi\cdot \vec{n}$ are both bounded in $B_{\varepsilon}$. Also, by AM-GM
\[\int_{B_{\varepsilon}}\frac{1}{|r|^{n-2}}dx=\int_{B_{\varepsilon}}\frac{1}{\left|\sqrt{\sum x_i^2}\right|^{n-2}}dx\le\int_{B_{\varepsilon}}\frac{1}{|\prod x_i|^{\frac{n-2}{n}}}dx\le \prod\left(\int_{-\epsilon}^{\epsilon}\frac{dx_i}{|x_i|^{\frac{n-2}{n}}}\right)\to 0 \mbox{ as $\varepsilon\to 0$}\]
We obtain $\int_{B_{\varepsilon}}\Gamma dx$ converges to zero while $\varepsilon\to0$.
So the only term that does not vanish is $\int_{\partial B_{\varepsilon}}\nabla\Gamma\cdot \vec{n}\varphi d\sigma$.
Obviously \[\nabla\Gamma\cdot \vec{n}=\frac{\partial}{\partial r}\Gamma=-\frac{1}{|S^{n-1}||x|^{n-1}}.\]
Which gives the following equality:
\[\lim_{\varepsilon\to 0}\int_{\partial B_\epsilon}-\frac{\varphi(x)}{|S^{n-1}||x|^{n-1}}dx=\lim_{\varepsilon\to 0}\int_{\partial B_\epsilon}-\frac{\varphi(x)}{|S^{n-1}||\varepsilon|^{n-1}}dx\]
By continuity of $\varphi(x)$ it is clear that this limit equals $-\varphi(0)$. That is
\[\int_{\mathbb{R}^{n}}-\Delta\Gamma(x)\varphi(x)dx=\varphi(0)\]
2.2 Spaces of functions
In this section we define some spaces that will aid our research of generalized functions.
Definition 2.A normed linear subspace is a linear space equipped with a norm, where the norm on a linear space $X$ is defined as s map $X\to \mathbb{R}$ such that
- $\|x\|\ge 0,\|x\|=0$ iff $x=0$.
- $\|\lambda x\|=|\lambda|\|x\|$.
- $\|x+y\|\le\|x\|+\|y\|$.
A Banach space is a complete NLS.
The completion is given by "every Cauchy sequence converges" in the metric space.
Example 1. Let
\[L^p(\Omega)=\left\{f:\Omega\to\mathbb{R}\mid f\textrm{ is measurable, that is } \int_{\Omega}|f(x)|^pdx<+\infty\right\}\quad 1\le p\le \infty\]
with the norm $\|f\|_{L^p}:=(\int_{\Omega}|f(x)|^pdx)^{1/p}$When $p=\infty$, the norm is defined as
$\|f\|_{L^\infty}=\esssup_{x\in\Omega}|f(x)|$
And now we define the Hölder semi-norm:
Definition 3.We define $f\in C_{b}^{0,\alpha}(\Omega),(0<\alpha\le 1)$ if
\[[f]_{C^{\alpha}(\Omega)}=\sup_{x\not=y,x,y\in\Omega}\frac{|f(x)-f(y)|}{|x-y|^{\alpha}}<+\infty\]
(Homework 6)Prove that $\alpha>1$, $[f]_{C^{\alpha}(\Omega)}<\infty$ implies $f\equiv C$.
Proof:Since $\forall x,y\in\Omega$,
\[\frac{|f(x)-f(y)|}{|x-y|^{\alpha}}<c\]
And this constant is fixed and finite.So we take the definition of derivative:
for $x$ and $x+\epsilon$, where $\epsilon\to0$, we obtain:
\[|f'(x)|=\lim_{\epsilon\to 0}\frac{|f(x)-f(x+\epsilon)|}{|\epsilon|}<\lim_{\epsilon\to 0}c\epsilon^{\alpha-1}=0\]
This means for any point $x$, the derivative at $x$ exists and equals zero.This directly implies $f\equiv C$ for some $C$.$\square$
So we may derive the norm in Hölder space
\[\|f\|_{C^{k,\alpha}}=\sum_{|\beta|\le k}\|D^{\beta}f\|_{C^0(\bar{\Omega})}+\sum_{|\beta|= k}[D^{\beta}f]_{C^\alpha(\bar{\Omega})}\]
2.3 Weak Derivative
In this section, we will define the weak derivative that is extremely important in Sobolev space.
The weak derivative is somehow similar to the generalized derivative that we have defined before, but a slight difference is made.
Definition 4.For $f\in L_{loc}^{1}(\Omega)$,if there exists $v\in L^{1}_{loc}(\Omega)$ such that for all $\varphi\in C_{0}^{\infty}(\Omega)$ we have
\[(-1)^{|\alpha|}\int_{\Omega}f(x)D^{\alpha}\varphi(x)dx=\int_{\Omega}v(x)\varphi(x)dx\]
we say $v(x)$ is the $\alpha-$th weak derivative of $f$
Here we gave some examples to show the properties of weak derivative.
-
$\exists f\in L^{1}(-1,1)$ that $f$ is not weak differentiable
(Homework 7)Let $h(x)$ be
$$
h(x)=\left\{ \begin{array}{rl}
0 \quad (x\le 0)\\
1 \quad (x>0)
\end{array} \right.
$$
prove that it is not weak differentiable.
Proof:If weak derivative exists, denoted by $u$, $\forall \varphi\in C_{0}^{\infty}(-1,1)$ we have
\[\int_{u}\varphi dx=\varphi(0).\]
Since $u$ is locally integrable, $\forall \varepsilon>0$, $\exists \delta>0$ such that $M(A)<\delta$, $\int_{A}|u|dx<\frac{1}{2}$. Where $M(\cdot)$ denotes the measure of a set.So we take
$$
\varphi_{\delta}(x)=\left\{ \begin{array}{rl}
0 \quad (|x|\ge \frac{\delta}{2})\\
e^{-\frac{|x|}{\delta^2-4|x|^2}} \quad (|x|<\frac{\delta}{2})
\end{array} \right.
$$
Obviously, $\varphi_{\delta}\in C_{0}^{\infty}(-1,1)$, $|\varphi_{\delta}(x)|\le1$.
That is
\[1=\varphi(0)=\int_{-1}^{1}u\varphi_{\delta}dx\le\int_{-\delta}^{\delta}|u||\varphi_{\delta}|dx\le\int_{-\delta}^{\delta}|u|dx\le\frac{1}{2}\]
Which makes a contradiction.$\square$ - The two weak derivative of $f$ are equal almost everywhere. That is $D^{\alpha}f=v$,$D^{\alpha}f=u$,$u,v\in L_{loc}^{1}(\Omega)\Rightarrow u=v$ a.e.
-
(Homework 8)$D^{\alpha} f=u, D^{\alpha} f=v$, show that $u=v$ a.e.
Proof:Since $\int_{\Omega}(u(x)-v(x))f(x)dx\equiv 0$ for all $f\in C_{0}^{\infty}(\Omega)$, by the next homework we know that it is true. -
(Homework 9)
Weak derivative satisfies the testing principle, that is $f\in L_{loc}^{1}(\Omega)$, if \[\int_{\Omega}f(x)\varphi(x)dx=0\] holds $\forall \varphi\in C_{0}^{\infty}(\Omega)$, then $f=0$ a.e.
Proof:Easily, there exists sequence $ \phi_n \in C^\infty_c(\Omega) $ such that $ \phi_n \rightarrow \chi_{B(x,r)} $ locally uniformly.For sufficiently large $n$ if all $\phi_n $ are supported inside $K$ then you have the estimate for any $\epsilon >0 $
$$ \left|\int_\Omega (f\phi_n - f\chi_{B(x,r)})dx \right| \leq \int_\Omega |f||\phi_n - \chi_{B(x,r)}|dx \leq \epsilon\|f\|_{L^1(K\cap B(x,r))} $$
But as $\int_\Omega f\phi_n dx = 0 $ hence $\int_\Omega f\chi_{B(x,r)} dx = 0 $.
Considering lebesgue differentiation theorem,
\[f=\lim_{\delta\to 0}\frac{1}{|B(x,\delta)|}\int_\Omega ( f\chi_{B(x,r)})dx=0 \mbox{ a.e.}\].
3.Sobolev space and its properties
3.1 Basic ideas
When the definition of weak derivatives is finished, we may come to our final goal: the study of Sobolev space.
Definition 5.The Sobolev space is defined as follows:
\[W^{k,p}(\Omega)=\left\{f\in L^{p}(\Omega)|\forall \alpha,|\alpha|\le k, D^{\alpha}f \textrm{ exists as weak derivative and }\sum_{|\alpha|\le k}\int_{\Omega}|D^{\alpha}f|^{p}dx<\infty \right\}\]
Naturally, the norm of this space is defined as
\[\|f\|_{W^{k,p}(\Omega)}=\left(\sum_{|\alpha|\le k}\int_{\Omega}|D^{\alpha}f|^{p}dx\right)^{\frac{1}{p}}\cong \sum_{|\alpha|\le k}\left(\int_{\Omega}|D^{\alpha}f|^{p}dx\right)^{\frac{1}{p}}\]
Specially, $p=2$, $W^{k,p}(\Omega)\equiv H^{k}(\Omega)$.
To show the goodness of this space ,we may first show its completeness under this norm. That is , it is a Banach space.
Theorem 2.The Sobolev space $W^{k,p}(\Omega)$ is a Banach space.
Proof:The outline of the proof is shown as follows:
- Sobolev norm is really a norm.
- If $\{f_m\}_{m=1}^{\infty}$ is a Cauchy sequence in $W^{k,p}$, then $\{D^{\alpha}f_{m}\}_{m=1}^{\infty}$ is a Cauchy sequence in $L^p$.
- $D^{\alpha}f_{m}$ converges to $f_{\alpha}$ in $L^p$, thus $D^{\alpha}f=f_{\alpha}$, and $f_m\to f$.
So we may begin our proof.
For 1, Linearity and positivity is clear. To show the triangle inequality, we may use the Minkowski's inequality and done.
For 2,If a Cauchy sequence in $W^{k,p}$ is constructed, name $\{f_m\}_{m=1}^{\infty}$. $\forall$ index $\alpha$, $|\alpha|\le k,D^{\alpha}f_n\in L^p$ and
\[\|D^{\alpha}f_n-D^{\alpha}f_m\|_{L^p}\le\|f_n-f_m\|_{W^{k,p}}\to 0\]
By completeness of $L^p$, we have $f_m\to f$ in $L^p$ as well as $D^{\alpha}f_m\to f_{\alpha}$ in $L^p$.
For 3,We may first check that $D^{\alpha}f=f_{\alpha}$, thus $f\in W^{k,p}$.
Observing that \[D^{\alpha}f(\varphi)=(-1)^{|\alpha|}\int_{\Omega}f(x)D^{\alpha}\varphi(x) dx=\lim_{n\to\infty }(D^{\alpha}f_n)(\varphi(x))=f_{\alpha}(\varphi(x))\]
We know that $D^{\alpha}f=f_\alpha\in L^p$. Thus $f\in W^{k,p}$, and $D^{\alpha}f=f_{\alpha}$ for all $|\alpha|\le k$.
Since $D^{\alpha}f=f_{\alpha}$, it's obvious that $\|f_n-f\|_{W^{k,p}}\to 0$ by the addition of $|D^{\alpha}(f_n-f)|$ all converges to zero.$\square$
We may now define a useful operator, named "mollifier", to continue our journey to the studying of Sobolev space.
First, we define the weight function,
Definition 6.We call $\rho(x)$ to be a weight function if it satisfies:
- $\rho(x)\ge 0,\int_{\mathbb{R}^n}\rho(x)dx=1$
- $\rho(x)\in C_{0}^{\infty}(\mathbb{R}^n)$
- $\rho(x)=0$ if $|x|\ge 1$
As an example,
$$
\rho(x)=\left\{ \begin{array}{rl}
0 \quad (|x|\ge 1)\\
C_n e^{-\frac{1}{1-|x|^2}} \quad (|x|<1)
\end{array} \right.
$$
is a weight function, where $C_n$ is the normalizing constant related to dimension $n$.
We define a new function $\rho_{\varepsilon}(x)$ if we have $\rho(x)$ in hand, that is
\[\rho_{\varepsilon}(x)=\frac{1}{\varepsilon^n}\rho\left(\frac{x}{\varepsilon}\right)\]
This function has a good quality, that it can smoothen the functions that is originally really "bad". The convolution with $\rho_{\epsilon}$ can make the new function $C^{\infty}$, and as $\varepsilon\to 0$, the new function will converges to zero.
So we define the "mollifier" to be the operator, given by
Definition 7.$A_{\varepsilon}:L^p(\Omega)\to L^p(\Omega)$ with
\[A_{\varepsilon}(u)=u_{\varepsilon}(x)=(\rho_{\varepsilon}\star u)(x)=\int_{B_{\varepsilon}}u(x-y)\rho_{\varepsilon}(y)dy\]
The mollifier has the following properties:
- $\|A_{\varepsilon}u\|_{L^p}\le\|u\|_{L^p}$, which is a version of Minkowski's inequality.
- $u$ is continuous, $A_{\epsilon}u\to u$ uniformly on a compact subset.
-
(Homework Optional) $\|A_{\varepsilon}u- u\|_{L^{p}(\Omega)}\to 0$ as $\varepsilon\to 0$ when $\forall u\in L^p(\Omega)$
Proof:What we need to find is that
\[\lim_{\varepsilon\to 0}\|u-\rho_{\varepsilon}\star u\|_{L^p}=0\]
Since
\begin{align*}
|u(x)-\rho_{\varepsilon} \star u(x)|&= \left|\int_{\mathbb{R}^n}\rho_{\varepsilon}(y)(u(x-y)-u(x))dy\right|\\\
&\leq \int_{\mathbb{R}^n}\rho_{\varepsilon}(y)|u(x-y)-u(x)|dy\end{align*}
Thus
\begin{align*}
|u(x)-\rho_{\varepsilon} \star u(x)|^p&\leq \left(\int_{\mathbb{R}^n}\rho_{\varepsilon}(y)|u(x-y)-u(x)|dy\right)^p\\
&\le \int_{\mathbb{R}^n}\rho_{\varepsilon}(y)|u(x-y)-u(x)|^pdy\end{align*}
By Fubini's theorem, we know that
\begin{align*}\|u(x)-\rho_{\varepsilon} \star u(x)\|_{L^p}&\le \int_{\mathbb{R}^n}\int_{\mathbb{R}^n}\rho_{\varepsilon}(y)|u(x-y)-u(x)|^p dy \\ dx&=\int_{\mathbb{R}^n}\int_{\mathbb{R}^n}\rho_{\varepsilon}(y)|u(x-y)-u(x)|^p dx dy\\
&=\int_{\mathbb{R}^n}\|u^y-u\|_{L^p}^p\rho_{\varepsilon}(y) dy
\end{align*}
where $u^y(x)=u(x-y)$. Let $v(y)=\|u^y-u\|_{L^p}^p$.It's obvious that $g(0)=0$, and $g$ is bounded since
\[v(y)\le \|u^y\|_{L^p}+\|u\|_{L^p}=2\|u\|_{L^p}\]
Continuing the computation, we find
\[\|u(x)-\rho_{\varepsilon} \star u(x)\|_{L^p}\le \int_{\mathbb{R}^n}g(\varepsilon s)\rho(s) ds\]
Since $\varepsilon\to 0,g(\varepsilon s)\rho(s) \to g(0)\rho(s)$ point wise on $\mathbb{R}^n$, and the integrand is bounded since $|g(\varepsilon s)\rho(s)|\le \|g\|_{\infty}\rho(s)$. So by Dominated Convergence Theorem we know that
\[\lim_{\varepsilon\to 0}\int_{\mathbb{R}^n}g(\varepsilon s)\rho(s) ds =0\]
That is \[\lim_{\varepsilon\to 0}\|u-\rho_{\varepsilon}\star u\|_{L^p}=0.\] -
(Homework 10) $\|A_{\varepsilon}-I\|\ge 1$
(Actually, I think $\|A_{\varepsilon}-I\|\to 0$ as $\varepsilon\to 0$, I don't know whether this is an error caused by understanding of this homework or caused by wrong calculation.. )
NonProof:The statement does not hold in $L^1$, because
we have
\begin{align*}
|u(x)-\rho_{\varepsilon} \star u(x)|&= \left|\int_{B(0,\varepsilon)}\rho_{\varepsilon}(y)(u(x-y)-u(x))dy\right|\\\
&\leq \int_{B(0,1)}\rho(t)(u(x-\varepsilon t)-u(x))dt\\\
&\leq \int_{B(0,1)}\rho(t)\sum_{j=1}^n\int_0^1\left|\frac{\partial u}{\partial x_j}(x-\varepsilon ts)\right|dsdt,
\end{align*}
and integrating over $\mathbb R^n$ (in fact a compact subset)
\begin{align*}
\lVert u -\rho_{\varepsilon} \star u(x)\rVert_1 &\leq\int_{B(0,1)}\rho(t)\sum_{j=1}^n\int_0^1\int_{\mathbb R^n}\left|\frac{\partial u}{\partial x_j}(x-\varepsilon ts)\right|dxdsdt\\\
&=\varepsilon\int_{B(0,1)}\rho(t)\int_0^1\sum_{j=1}^n\int_{\mathbb R^n}\left|\frac{\partial u}{\partial x_j}(\varepsilon x'-\varepsilon ts)\right|dx'dsdt\\\
&\leq \varepsilon \int_{B(0,1)}\rho(t)\int_0^1\lVert u\rVert_{1,1}dsdt\\\
&= \varepsilon \lVert u\rVert_{1,1}.
\end{align*}
That is to say \[\|A_{\varepsilon}-I\|_{L^1}\le \varepsilon\]
The following theorems are the key in Sobolev spaces, which gave the clear view of the space itself with respect to other function spaces. These four theorems are:
- Density Theorem, which states that $C^{\infty}$ is dense in Sobolev space.
- Extension Theorem, which claims that the function in a Sobolev space in $U$ can be extended to $\mathbb{R}^n$.
- Embedding Theorem, consider Sobolev space embedded into other spaces.
- Compact embedding, gave stronger condition to the embedding statements.
3.2 Density Theorem
Theorem 3 $C^{\infty}(\Omega)\cap W^{k,p}(\Omega)$ is dense in $W^{k,p}(\Omega)$
To prove this theorem, first note that we have $\rho_{\varepsilon}\star u$ can approximate $u$ in $L^p$ space as well as $W_{loc}^{k,p}(\Omega)$. However, this assertion does not hold in $W^{k,p}(\Omega)$, because the function is not always locally integrable, so we need the localization and unit partition technique to resolve the problem.
Proof:First, we denote $\Omega_{\varepsilon}=\{x\in\Omega|d(x,\partial\Omega)>\varepsilon\}$, $V_{j}=\Omega_{\frac{1}{2^{n+2}}}\backslash \Omega_{\frac{1}{2^{n-1}}}$
It is obvious that
\[\Omega = \bigcup_{n=1}^{\infty}V_{n}\]
We may do the approximation on each $V_n$.
We choose some functions $\varphi_n$, satisfying these properties:
- $\supp \varphi_n \subset V_n$,$\varphi_n=1$ on $\Omega_{\frac{1}{2^n}}\backslash\Omega_{\frac{1}{2^{n-1}}}$
- $0\le\varphi_n\le 1,\varphi_n\in C^{\infty}$
- $\sum_{n=1}^{\infty}\varphi_n <+\infty$(This can be satisfied since we can scale it to a proper size.)
We denote
\[\varphi(x)=\sum_{n=1}^{\infty}\varphi_n(x)\]
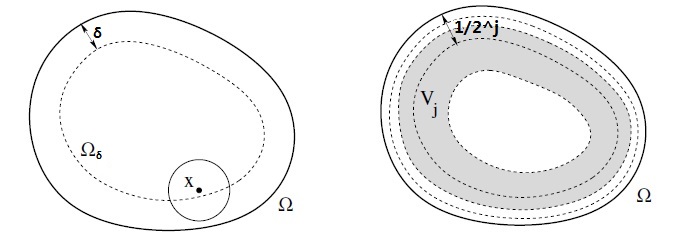
Here we let $\psi_n(x)=\frac{\varphi_n(x)}{\varphi(x)}$. Let $u^n(x)=u(x)\psi_n(x).$ By simple calculation, we know
\[u(x)=\sum_{n=1}^{\infty}u^n(x)\]
$u^n\in W^{k,p}(\Omega)$, as well as $u^n(x) \equiv 0$ when $x\not\in \Omega\backslash V_n$. By what we have proved before, we know that $\forall \varepsilon_n>0$, $\exists \delta_n>0$ such that
\[\|\rho_{\delta_n}\star u^n(x)-u^n(x)\|_{W^{k,p}}<\varepsilon_n\]
We take $\varepsilon_n=\frac{\varepsilon}{2^{n}}$, $w^n(x)=\rho_{\delta_n}\star u^n(x)$, and define
\[u_{\varepsilon}=\sum_{n=1}^{\infty}\rho_{\delta_n}\star u^n(x)\]
We have
\[\|u_{\varepsilon}-u\|_{W^{k,p}}\le\sum_{n=1}^{\infty}\|w^n-u^n\|_{W^{k,p}}\le\sum_{n=1}^{\infty}\frac{\varepsilon}{2^{n}}\le \varepsilon\]
For $\forall\varepsilon>0$, we can find this $u^{\varepsilon}$. Since the norm is finite, $u^{\varepsilon}\in W^{k,p}(\Omega)$. Since there is only finitely many $w^n\not=0$ in $V_n$, $u^{\varepsilon} \in C^{\infty}(\Omega)$. So the theorem is proved.$\square$
In the former proof, we makes the $W^{k,p}(\Omega)$ into countable $W^{k,p}_{loc}(\Omega)$ to generalize the problem. In the next theorem, we may generalize the problem into the closure of the set. But such generalization requires some restriction of the boundary.
Theorem 4.$C^{\infty}(\bar{\Omega})$ is dense in $W^{k,p}(\Omega)$ for $\Omega$ is bounded and $\partial \Omega$ is $C^1$
Why should the boundary be $C^1$? The reason is that we should "give place to" the mollifiers. Since the boundary which is $C^1$ has the following property:
The boundary of the area can be represented by a function, that is
\[x_n=\gamma(x_1,x_2,\cdots,x_{n-1})\]
If $x_n>\gamma(x_1,x_2,\cdots,x_{n-1})$, $x\in \Omega$. This can help us extend the function to a bit outside of the region, which require the $C^1$ condition.
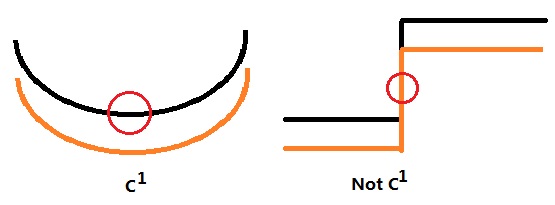
The left one is $C^1$, when a move in the boundary can cover a ball on the boundary. When not $C^1$, as is shown on the right hand, may not cover the ball with a distance moved. So we may begin our proof:
Proof:
-
For a point on the boundary, say $x^0\in\partial U$, $\partial U$ is $C^1$ and by inverse function theorem we know there exists an $C^1$ function $x_n=\gamma(x_1,x_2\cdots x_{n-1})$, where $x_i$ denotes the coordinate of $x$. And we represent the interior of the region, name $\Omega$, by
\[U=\Omega\cap B(x^0,r)=\{x_n>\gamma(x_1,x_2\cdots x_{n-1})\}\]
We let $V=\Omega \cap B(x^0,r)$, which gave the place for us to extending the function to somehow outside of the region. -
Then we use the shifted point to define the function outside the region: by scaling the moving the point,
\[x^{\varepsilon}:=x+\lambda \varepsilon e_n \quad(x\in V,\varepsilon>0)\]
we can get a sufficiently large $\lambda$ for $\forall x\in V$ and all $\varepsilon>0$, $B(x^{\varepsilon},\varepsilon)\subset U$.(PS:this $\lambda $ exists because of the $C^1$ condition.)We now use $u_{\varepsilon}(x):=u(x^{\varepsilon}),x\in V$ to approximate the original function, here the point in $V$ was transferred a bit into the region. We write $v^{\varepsilon}=\eta_{\varepsilon}\star u_{\varepsilon}$. So easily, we see that $v^{\varepsilon}\in C^{\infty}(\bar{V})$
-
We may claim that $v^{\varepsilon}\to u$ in $W^{k,p}(V)$, here we note that
\[\|D^{\alpha}v^{\varepsilon}-D^{\alpha}u\|_{L^p}\le\|D^{\alpha}v^{\varepsilon}-D^{\alpha}u_{\varepsilon}\|_{L^p}+\|D^{\alpha}u_{\varepsilon}-D^{\alpha}u\|_{L^p} \]
Note that the former is a natural approximation we have proved, the latter is only a slight move, so the claim that $v^{\varepsilon}\to u$. -
Since $\partial \Omega$ is compact, we know that there exist a finite cover with it with sphere with center $x_i^0$ and region $V_i$.Satisfying
\[\|v_i-u\|_{W^{k,p}(V_i)}\le\delta\]
Take $V_0\subset\subset \Omega$. With $\Omega \subset \cup_{i=0}^{N}V_i$. With the former theorem, there exist $v_0\in C^{\infty}(\bar{V_0})$ to approximate the $u$, say
\[\|v_0-u\|_{W^{k,p}(V_0)}\le\delta\] -
We define the approximating
\[v=\sum_{i=0}^{N}\psi_i v_i\]
where $\sum\zeta_i =1$. This is also a partition of space technique we have used before, by similar calculation
\[\|D^{\alpha}v-D^{\alpha}u\|_{L^p}\le\sum_{i=0}^{N}\|D^{\alpha}(\psi_i v_i)-D^{\alpha}\psi_i u\|_{L^p}\le C\sum_{i}^{N}\|v_i-u\|_{W^{k,p}}\le CN\delta\]
which proves the theorem.$\square$
3.3 Extension theorem
Here we state the extension theorem for Sobolev space, that a function in Sobolev space $W^{k,p}(\Omega)$ can be extended to $W^{k,p}(\mathbb{R})$.
Theorem 5.Assume $U$ is bounded, and $\partial U$ is $C^1$, $U\subset\subset V$ as $V$ is open. Then there exists a bounded linear operator:
\[E:W^{1,p}(U)\to W^{1,p}(\mathbb{R}^n)\]
satisfying the following conditions:
- $Eu=u$ a.e. in $U$.
- $\supp Eu\subset K\subset\subset U$.
- $\|E(u)\|_{W^{1,p}(V)}\le C\|u\|_{W^{1,p}(U)}$.
Note that we have the dense extension theorem:
Theorem 6.(Dense Extension Theorem)
$D\subset X$, where $X$ is a normed vector space, $Y$ is a Bananch space, $D$ is dense in $X$.
If $\exists A:D\to Y$ such that
\[\|Ax\|_{Y}\le C\|x\|_{X}\quad \forall x\in D\]
Then $\exists \bar{A}:X\to Y$ such that
\[\|\bar{A}x\|_{Y}\le C\|x\|_{X}\quad \forall x\in X\]
and $\bar{A}x=Ax$ $\forall x\in D$
Since we have the former theorems ,say, Dense Extension Theorem and the density theorem, the proof of the extension theorem is only to define the $E(u)$ for $u\in C^1(\bar{u})$.
The sketch for finding the linear operator is as follows:
- Chop off the boundary, and divide the boundary into localized ones, just as what we have done before in the density theorem, say, $u=\sum u_n$, where $u_n$ is defined on the localized circle near the boundary.
- Flattening the boundary, making it a plane which is easy to be discussed.
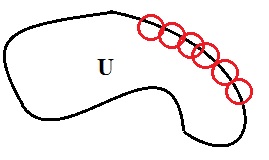
-
Working on the flattened space, find the function that is equal to the original function in the original set, and extend to the outside with another function, with the derivative on the boundary being well-defined.
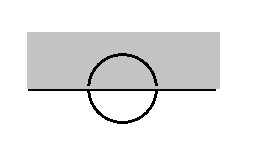
- Use compactness of boundary to say there is a global operator.
- Since the former only prove its correctness of the approximation in $C^{\infty}$ space, we may use the density theorem to prove its correctness in Sobolev space.
Here we show the proof of the theorem:
Proof:
-
First, we look at the function with a flat boundary:
We may assume that the boundary is given by $x_n>0,x\in U$ and $x_n<0,x\not\in U$, the boundary is $x_n=0$. We denote $x'$ be $x1,x2\cdots x_{n-1}$. The extension operator should obey:
\[E(u)(x',x_n)=\left\{ \begin{array}{rl}
u(x',x_n) &\quad x_n\ge 0
\\ \sum_{i=1}^{J} \alpha_i u(x',\lambda_i x_n) &\quad x_n<0
\end{array} \right.\]
Where $\sum \alpha_i=1$. Here we want $u_{x_n}^{-}=u_{x_n}^{+}$, that is
\[\frac{\partial u}{\partial x_n}(x',0)=\sum_{i=1}^{J}-\lambda_i\alpha_i\frac{\partial u}{\partial x_n}(x',0)\]
which immediately implies
\[\sum_{i=1}^{J}\lambda_i\alpha_i=-1\]
As an easy example, we let $J=2,\lambda_1=\frac{1}{2},\lambda_2=2$, obvious calculation implies $\alpha_1=2,\alpha_2=-1$.Here it is easy to check the inequality estimation:
\[\|u\|_{W^{1,p}(B)}\le C\|u\|_{W^{1,p}(B^+)}\]
where $B$ denotes the whole set of circle, $B^+$ denotes the circle intersect the original set. This is obvious since $\alpha_1,\alpha_2$ are all finite. -
Second, we may try to transform the non flat planes into flat ones, this is rather easy since the boundary is $C^1$, so we can find a $C^1$ mapping that flatten the boundary. The new function on $y$ is given by
\[y=\Phi(x),x=\Psi(y),\tilde{u}=u(\Psi(y))\]
Converting back to the x-coordinate, it's easy to see that inequality:
\[\|u\|_{W^{1,p}(w)}\le C\|u\|_{W^{1,p}(U)}\]
also holds, here $W$ denotes the converting back set. -
By the compactness of the boundary, there is a finite cover, thus we may extend the function to the union of $W_i$. We can use the technique we have used before, that is find a set of $C^{\infty}$ function with total $1$, denoted by $\psi_n(x)$. And
\[\bar{u}=\sum_{i=1}^{n} \psi_i \tilde{u}_i\]
is what we want. It's simple to see that this operator is linear. And the it satisfies:
\[\|\bar{u}\|_{W^{1,p}(\mathbb{R}^n)}\le C\|u\|_{W^{1,p}(U)}\] -
To show that correctness in Sobolev space, note that
$u_n$ in $C^{\infty}(\bar{U})$ converging to $u$ in $W^{1,p}(U)$, by linearity it implies
\[\|Eu_n-Eu_l\|_{W^{1,p}(\mathbb{R}^n)}\le C\|u_m-u_l\|_{W^{1,p}(U)}\]
Which is a Cauchy sequence. By completeness, the theorem is done.$\square$
Here we present an example:
(Homework 11)$f(x)\in C^{3}([0,1])$, extend it to $\tilde{f}(x)$, where $\supp \tilde{f} \subset[-\delta, 1+\delta]$
Proof:
We use the similar method in the former proof of the theorem.
First, we extend the function $f$ to $[-2\delta,1+2\delta]$ with also $C^n$, this can be realized because we can use the similar approximation near $0$, where $x<0$,
\[\bar{f}(x)=\sum_{i=1}^{n}\alpha_i f(w_i x)\]
with $\sum_{i=1}^{n} \alpha_i =1$. $w_i$ s can soon be solved by the number of equations is smaller than the number of variables. By similar way we can analyze the function on $x=1$.
Secondly, we take $\psi(x)=\rho_{\delta}\star\chi_{[-\delta,1+\delta]}$, and we use the multiplication:
\[\tilde{f}(x)=\bar{f}(x)\psi(x)\]
This is $C^3$ by $\psi$ is infinitely differentiable, $\psi(x)\equiv 1$ when $0\le x\le1$(Obvious). So $f(x)=\tilde{f}(x)$ in $x\in [0,1]$. Moreover, $\tilde{f}$ has support in $[-\delta,1+\delta]$ since $\psi(x)=0$ when $x\le -\delta$ or $x>-\delta$. So $\tilde{f}$ is the extension.$\square$
3.4 Sobolev Embedding Theorem
Before the Sobolev type inequality, first we may study the Hölder inequality:
Theorem 7(The Hölder inequality)
$1\le p,q\le \infty$ with $1/p+1/q=1$. Then, for all measurable real- or complex-valued functions f and g on the set $\Omega$,
\[\|fg\|_1\le\|f\|_p\|g\|_q\]
(Homework 12)
Generalization:
$p_i\ge 1$ and $\sum_{i=1}^{n}\frac{1}{p_i}=1$. Show that
\[\int_{\Omega}\left|\prod_{i=1}^{n}f_i(x)\right|\le\prod_{j=1}^{n}\|f\|_{p_i}\]
Proof:By induction, we know $n=1$ it holds, when $n-1$ holds, we would like to generalize it into $n$. We can then divide them into two cases
-
If $p_n=\infty$, then
\[\sum_{k-1}^{n-1}\frac{1}{p_k}=1\]
So\[\left\|\prod_{i=1}^{n}f_i\right\|_1\le\left\|\prod_{i=1}^{n-1}f_i\right\|_1\|f_n\|_{\infty}\le\prod_{i=1}^{n}\|f\|_{p_i}\] -
If $p_n<\infty$, then we let $p=\frac{p_n}{p_n-1}$,$q=p_n$, we have
\[\left\|\prod_{i=1}^{n}f_i\right\|_1\le\left\|\prod_{i=1}^{n-1}f_i\right\|_p\|f_n\|_q\le\left(\left\|\prod_{i=1}^{n-1}f_i^p\right\|_1\right)^{\frac{1}{p}}\|f_n\|_{p_n} \]
We let $p_i'=p_i/p$, so $\sum p_i'=1$, the inequality becomes
\[\left(\left\|\prod_{i=1}^{n-1}f_i^p\right\|_1\right)^{\frac{1}{p}}\|f_n\|_{p_n} \le \left(\prod_{i=1}^{n-1}\left\|f_i^p\right\|_{p_i'}\right)^{\frac{1}{p}}\|f_n\|_{p_n}=\prod_{i=1}^{n-1}\left\|f_i^{p_i'}\right\|_{p_i}\|f_n\|_{p_n}=\prod_{i=1}^{n}\|f\|_{p_i}\]
By the inequality before, we can now state our Sobolev inequality, which is the most fundamental theory in Sobolev space.
The Gagaliardo-Nirenberg-Sobolev inequality is shown as follows:
Theorem 8.Assume $1\le p<n$, $u\in C_{0}^{1}(\mathbb{R}^n)$, then
\[\|u\|_{L^{p^*}(\mathbb{R}^n)}\le C(n,p)\|\nabla u\|_{L^p(\mathbb{R^n})}\]
where $1/p^{*}=1/p-1/n$, $C$ is a constant depending on $n$ and $p$.
Proof:To prove this theorem, we may first prove the easiest case:
$p=1,n=2$. We get $p^{*}=1$
$u(x_1,x_2)=\int_{-\infty}^{x_2}u_{x_2}(x_1,y_2)dy_2$. So
\[|u(x_1,x_2)|\le\int_{-\infty}^{x_2}|u_{x_2}(x_1,y_2)|dy_2\le\int_{-\infty}^{\infty}|u_{x_2}(x_1,y_2)|dy_2 \]
Also, by similar way, we get
\[|u(x_1,x_2)|\le\int_{-\infty}^{\infty}|u_{x_1}(y_1,x_2)|dy_1\]
Thus
\begin{align*}
\|u\|_{L^2(\mathbb{R}^2)}& =\iint_{\mathbb{R}^2}|u(x_1,x_2)|^2 dx_1dx_2 \le \iint_{\mathbb{R}^2}\left(\int_{-\infty}^{\infty}|u_{x_1}(y_1,x_2)|dy_1\int_{-\infty}^{\infty}|u_{x_2}(x_1,y_2)|dy_2\right) dx_1dx_2
\\&=\left(\iint_{\mathbb{R}^2} |u_{x_2}(x_1,y_2)|dy_2 dx_1\right)\left(\iint_{\mathbb{R}^2} |u_{x_1}(y_1,x_2)|dy_1 dx_2\right)
\\&\le \left(\iint_{\mathbb{R}^2} |\nabla u|dx_2 dx_1\right)^2=\|\nabla u\|_{L^1(\mathbb{R}^2)}
\end{align*}
This case is thus proven.
Consider $p=1,n=3$, we get $p^*=\frac{3}{3-1}=\frac{3}{2}$.
By similar way as before, we get
\[|u(x)|\le \int_{\mathbb{R}} |u_{x_i}(\hat{x}|_{x_i\to y_i})| dy_i\le \int_{\mathbb{R}} |\nabla u(\hat{x}|_{x_i\to y_i})| dy_i \]
When $\hat{x}|_{x_i\to y_i}$ denotes that $x_i$ is replaced by $y_i$.
Thus
\[|u(x)|^3\le \prod_{i=1}^{3}\int_{\mathbb{R}}|\nabla u(\hat{x}|_{x_i\to y_i})| dy_i\]
We use this inequality, thus
\begin{align*}\int_{\mathbb{R}}|u(x)|^{\frac{3}{2}}dx_{1}&\le \int_{\mathbb{R}}\left(\prod_{i=1}^{3}\int_{\mathbb{R}}|\nabla u(\hat{x}|_{x_i\to y_i})| dy_i\right)^{\frac{1}{2}}dx_1\\&=\left(\int_{\mathbb{R}}|\nabla u(\hat{x}|_{x_1\to y_1})| dy_1 \right)^{\frac{1}{2}}\left(\prod_{i=2}^{3}\iint_{\mathbb{R}^2}|\nabla u(\hat{x}|_{x_1\to y_1,x_i\to y_i})| dy_1 dy_i \right)^{\frac{1}{2}}\end{align*}
Integrating by $x_2$ again, we get
\[\iint_{\mathbb{R}^2}|u|^{\frac{3}{2}}dx_{1}dx_2 \le \left(\iint_{\mathbb{R}^2}|\nabla u(\hat{x}|_{x_1\to y_1,x_2\to y_2})| dy_1 dy_2 \right) \left(\iiint_{\mathbb{R}^3}|\nabla u(\hat{x}|_{x_1\to y_1,x_2\to y_2,x_3\to y_3})| dy_1 dy_2 dy_3 \right)^{\frac{1}{2}} \]
Easily we see that
\[\iint_{\mathbb{R}^2}|u|^{\frac{3}{2}}dx_{1}dx_2 dx_3\le \left(\iiint_{\mathbb{R}^3}|\nabla u(\hat{x}|_{x_1\to y_1,x_2\to y_2},x_3\to y_3)| dy_1 dy_2 dy_3 \right)^{\frac{3}{2}} \]
The the case is proven.$\square$
(Homework Optional) Prove the $n=4$ case. $p^*=4/3$
Proof:Here the proof is similar, we get
\[|u(x)|\le \int_{\mathbb{R}}|\nabla u|(\hat{x}_{x_i\to y_i})dy_i\]
Thus
\[|u(x)|^4\le \prod_{i=1}^{4}\int_{\mathbb{R}}|\nabla u(\hat{x}|_{x_i\to y_i})| dy_i\]
Thus when we integrate via $x_1$, we get
\[\int_{\mathbb{R}}|u(x)|^{\frac{4}{3}}dx_1 \le \left(\int_{\mathbb{R}}|\nabla u|dx_1\right)^{\frac{1}{3}}\left(\prod_{i=2}^{4}\iint_{\mathbb{R}^2}|\nabla u|dx_1dy_i \right)^{\frac{1}{3}}\]
Then integrate via $x_2$, we get
\[\iint_{\mathbb{R}}|u(x)|^{\frac{4}{3}}dx_1 dx_2\le \left(\iint_{\mathbb{R}^2}|u(x)|dx_1dx_2\right)^{\frac{2}{3}}\left(\prod_{i=3}^{4}\iiint_{\mathbb{R}^3}|\nabla u|dx_1dx_2 dy_i \right)^{\frac{1}{3}} \]
Integrating via $x_3$, we get
\[\iiint_{\mathbb{R}^3}|u(x)|^{\frac{4}{3}}dx_1 dx_2 dx_3 \le \left(\iiint_{\mathbb{R}^3}|u(x)|dx_1dx_2dx_3\right) \int_{\mathbb{R}^4}|\nabla u|dx_1dx_2dx_3dx_4\]
Integrating via $x_4$, hence the result is
\[\|u(x)\|_{L^{\frac{4}{3}}(\mathbb{R})} \le\|\nabla u\|_{L^4(\mathbb{R})}\]
To prove the general $n$, we note that a step of integral has taken all of $x_1,x_2\cdots x_n$ if we integrate them $n$ times ,and the the $|\nabla u|dy_i$ all becomes $|\nabla u|dx_1 dx_2\cdots dx_n$.
By similar way, we know that
\[\int_{\mathbb{R}^n}|u|^{\frac{n}{n-1}}dx\le \left(\int_{\mathbb{R}^n}|\nabla u|dx\right)^{\frac{n}{n-1}}\]
To prove the general $1<p<n$. We apply it to $v=|u|^{\frac{np}{n-p}}$ to transform it into $p=1$ case:
We should note that
(Homework 13) $u\in C_0^1(\mathbb{R}^n)$ implies $|u|^\gamma(x)\in C_0^1(\mathbb{R}^n), (\gamma >1)$
This can be verified by taking derivative, since
\[\nabla|u|^\gamma = \gamma |u|^{\gamma-1} \nabla u\]
Hence it is $C^1$, and has value $0$ on the boundary.
So we should choose $\gamma>1$ such that it will give the correct answer, that is
\[\left(\int_{\mathbb{R}^n}|u|^{\frac{\gamma n}{n-1}}\right)^{\frac{n-1}{n}}\le \int_{\mathbb{R}^n}\gamma |u|^{\gamma-1} |\nabla u|dx \le \left(\int_{\mathbb{R}^n}|u|^{(\gamma-1)\frac{p}{p-1}}dx\right)^{\frac{p-1}{p}}\left(\int_{\mathbb{R}^n}|\nabla u|^p dx\right)^{\frac{1}{p}} \]
So we select
\[\gamma =\frac{p(n-1)}{n-p}>1\]
and the proof is done.$\square$
The next theorem will demonstrate the embedding of $W^{1,p}$ into $L^{p^*}$. The theorem states the following truth:
Theorem 9.Let $\Omega$ be bounded,open subset in $\mathbb{R}^n$ and has $\partial \Omega$ be $C^1$. Then $\exists C>0$, that for any $u\in W^{1,p}(\Omega)$
\[\|u\|_{L^{\frac{np}{n-p}}(\Omega)}\le C\|u\|_{W^{1,p}(\Omega)}\]
The spirit of the proof is to approximate $u$ by the compact supported functions, and use the estimation we used before and get the desired result, here we present the proof:
-
By the extension theorem, $\exists E$ to be the extension function, and $Eu=\bar{u}\in W^{1,p}(B_R)$, as $\bar{\Omega}\in B_R$. By the extension theorem before, we know
\[\|E(u)\|_{W^{1,p}(B_R)}\le C\|u\|_{W^{1,p}(B_R)}\]
Also, we may use the mollifier to fulfill approximating our goal and finally prove it: -
$\rho_{\epsilon}\star E(u)\in C_{0}^{\infty}(\mathbb{R}^n)$ as
\[D^{\alpha}\left(\rho_{\epsilon}\star E(u)\right)=\rho_{\epsilon}\star D^{\alpha}E(u)\to D^{\alpha}E(u) \in L^p\]
Also, by what we have proven $\rho_{\epsilon}\star E(u) \to E(u)\in W^{1,p}$.We can claim that
\begin{align*}\|\rho_{\epsilon}\star E(u)\|_{L^{\frac{np}{n-p}}}&\le \gamma \|\nabla \rho_{\epsilon}\star E(u)\|_{L^p}=\gamma \| \rho_{\epsilon}\star \nabla E(u)\|_{L^p}\\&\le \gamma\|\nabla E(u)\|_{L^p(B_R)}\le\gamma \|E(u)\|_{W^{1,p}(B_R)}\le \gamma C\|u\|_{W^{1,p}(\Omega)}\end{align*}
So if we let $\varepsilon\to 0$, we get
\[\|u\|_{L^{\frac{np}{n-p}}(\Omega)}\le\|E(u)\|_{L^{\frac{np}{n-p}}(B_R)}\le \gamma C\|u\|_{W^{1,p}(\Omega)}\]
and the theorem is done.$\square$
We have achieved a byproduct by the proof before:
Theorem 10.Assume $u\in C^1(\mathbb{R}^n)$, then $$[u]_{C^{0,\gamma}(\mathbb{R}^n)}\le C\|\nabla u\|_{L^p(\mathbb{R}^n)}$$
for $n<p<\infty,\gamma=1-\frac{n}{p}$.
This inequality is called the Morrey's inequality. The inequality states that $W^{1,p}$ can be embedded into the H\"older space $C^1(\mathbb{R}^n)$.Sketch of the proof is proving three inequalities to get the result. The proof is given as follows:
Proof:First, we may prove that
(Homework 14)\[\dashint_{B(x,r)}|u(x)-u(y)|dy\le C\int_{B(x,r)}\frac{|\nabla u(y)|}{|y-x|^{n-1}}dy\]
To prove this lemma, we should first note that $\forall w\in \partial B(0,1)$, if $0<s<r$, we have
\[|u(x+sw)-u(x)|\le\left|\int_{0}^{s}\frac{d}{dt}u(x+tw)dt\right|\le\int_{0}^{s}|\nabla u(x+tw)|dt\]
Hence, we get
\begin{align*}\int_{\partial B(0,1)}|u(x+tw)-u(x)|dS&\le \int_{0}^{s}\int_{\partial B(0,1)}|\nabla u(x+tw)|dSdt\\&=\int_{0}^{s}\int_{\partial B(0,1)}|\nabla u(x+tw)|\frac{t^{n-1}}{t^{n-1}}dSdt\end{align*}
Let $y=x+tw$, so that $t=|x-y|$. Then from polar coordinate, we have
\[\int_{\partial B(0,1)}|u(x+sw)-u(x)|dS\le\int_{B(x,s)}\frac{|\nabla u(y)|}{|x-y|^{n-1}}dy\le\int_{B(x,r)}\frac{|\nabla u(y)|}{|x-y|^{n-1}}dy \]
Integrating from $0$ to $r$ we get
\[\int_{B(x,r)}|u(y)-u(x)|dy\le \frac{r^n}{n}\int_{B(x,r)}\frac{|\nabla u(y)|}{|x-y|^{n-1}}dy\]
Which gives the answer.
Then we give the proof of the theorem:
For $|u(x)|$,and $|x-y|<1$ we have
\begin{align*}
|u(x)|&\le \dashint_{B(x,1)}|u(x)-u(y)|dy+\dashint_{B(x,1)}|u(y)dy\\
&\le C\int_{B(x,r)}\frac{|\nabla u(y)|}{|x-y|^{n-1}}dy+C\|u\|_{L^p}\\
&=C\left(\int_{\mathbb{R}^n}|\nabla u|^pdy\right)^{\frac{1}{p}}\left(\int_{B(x,1)}\frac{1}{|x-y|^{\frac{(n-1)p}{p-1}}}dy\right)^{\frac{p}{p-1}}+C\|u\|_{L^p(\mathbb{R}^n)}\\
&\le C\|u\|_{W^{1,p}(\mathbb{R}^n)}
\end{align*}
The inequality holds by H\"older inequality and note that
\[\int_{B(x,1)}\frac{1}{|x-y|^{\frac{(n-1)p}{p-1}}}dy<\infty\]
So this implies
\[\sup_{\mathbb{R}^n}|u|\le C\|u\|_{W^{1,p}(\mathbb{R}^n)}\]
So we write $r=|x-y|$, and we have
\[|u(x)-u(y)|dy\le\dashint_{W}|u(x)-u(z)|dz+\dashint_{W}|u(y)-u(z)|dz\]
where $W=B_{R}(x)\cap B_R(y)$. Hence by similar method:
\begin{align*}
\dashint_{W}|u(x)-u(z)|dz &\le C\dashint_{B(x,r)}|u(x)-u(z)|dz\\
&\le C\left(\int_{B(x,r)}|du|^pdz\right)^{\frac{1}{p}}\left(\int_{B(x,r)}\frac{1}{|x-z|^{\frac{(n-1)p}{p-1}}}dz\right)^{\frac{p}{p-1}}
\\&\le C r^{1-\frac{n}{p}}\|\nabla u\|_{L^p(\mathbb{R}^n)}
\end{align*}
By this estimation, we get
\[|u(x)-u(y)|\le C r^{1-\frac{n}{p}}\|\nabla u\|_{L^p(\mathbb{R}^n)}=C|x-y|^{1-\frac{n}{p}}\|\nabla u\|_{L^p(\mathbb{R}^n)} \]
Thus
\[[u]_{C^{0,1-n/p}(\mathbb{R}^n)}=\sup_{x\not = y}\left\{\frac{|u(x)-u(y)|}{|x-y|^{1-n/p}}\right\}\le C \|\nabla u\|_{L^p(\mathbb{R}^n)} \]
Also, we have the extension of the theorem before, that is, the Sobolev space is embedded into its extension on $\bar{\Omega}$. The theorem states as follows:
Theorem 11.Let $\Omega$ be a bounded open subset of $\mathbb{R}^n$, and suppose $\partial \Omega$ is $C^1$. Then $\exists C(n,p,\Omega)$ such that for $u\in W^{1,p}(\Omega)$,there $\exists u^*$ we have
\[\|u^*\|_{C^{0,\gamma}}(\bar{\Omega}) \le C\|u\|_{W^{1,p}(\Omega)}\]
where $u^*=u$ a.e.
The spirit of this proof is really similar to the proof of Theorem 9, that is, first approximate by functions on other space, then use the estimation we have given before to get the result.
Proof:Because of the $C^1$ boundary of $\partial \Omega$, we can get an extension $Eu=\bar{u}\in W^{1,p}(\mathbb{R}^n)$ such that $\bar{u}=u$ in $\Omega$ and have compact support with inequality
\[\|\bar{u}\|_{W^{1,p}(\mathbb{R}^n)}\le C\|u\|_{W^{1,p}(\Omega)}\]
Since it has compact support, so there exist $\{u_m\}_{m=1}^{\infty}\in C_{0}^{\infty}(\mathbb{R}^n)$ to approximate it. That is
\[u_m\to \bar{u} \in W^{1,p}(\mathbb{R}^n)\]
Also, according to former theorem,$\{u_m\}_{m=1}^{\infty}$ is also a Cauchy sequence, thus $\exists u^*$, s.t.
\[u_m\to u^* \in C^{0,1-n/p}(\mathbb{R}^n)\]
So, it's easy to see that $u=u^*$ a.e. Since Theorem 4 provides us that
\[\|u_m\|_{ C^{0,1-n/p}(\mathbb{R}^n)}\le C \|u_m\|_{ W^{1,p}(\mathbb{R}^n)}\Rightarrow \|u^*\|_{ C^{0,1-n/p}(\mathbb{R}^n)}\le C \|u\|_{ W^{1,p}(\mathbb{R}^n)}\]
Hence we complete the proof.$\square$
The theorems all present us the good qualities of $W^{1,p}$, we can present the results we have got here:
$$
W^{1,p}(\Omega) \hookrightarrow\left\{ \begin{array}{lll}
L^q(\Omega) &\quad \frac{1}{q}=\frac{1}{p}-\frac{1}{n}\quad &1\le p<n
\\ C^{0,\gamma}(\bar{\Omega}) &\quad \gamma =1-\frac{n}{p}\quad & p>n\\
L^q(\Omega) &\quad q <\infty \quad &p=n
\end{array} \right.
$$
With $\Omega=\mathbb{R}^1$ or $\Omega\subset \mathbb{R}^1$ is bounded and has $C^1$ boundary.
We can now present the general case of Sobolev inequality,
Let $\Omega$ be a bounded open subset of $\mathbb{R}^n$, $\partial \Omega$ is $C^1$. Thus
$$
W^{k,p}(\Omega) \hookrightarrow\left\{ \begin{array}{lll}
L^q(\Omega) &\quad \frac{1}{q}=\frac{1}{p}-\frac{k}{n}\quad & kp<n
\\ C^{k-\lfloor\frac{n}{p}\rfloor-1,\gamma}(\bar{\Omega}) &\quad \gamma =\lfloor\frac{n}{p}\rfloor+1-\frac{n}{p}\quad & p>n\\
C^{k-\frac{n}{p}-1,\gamma}(\bar{\Omega}) &\quad 0<\gamma<1 \quad &p=n
\end{array} \right.
$$
To show the sharpness of some of the conditions, we present the example below:
(Homework 15)Show that \[W^{k,p}(\Omega) \not\hookrightarrow C^{k-\frac{n}{p}-1,1}(\bar{\Omega})\]
when $\frac{n}{p}$ is an integer.
Proof:Consider $\mathbb{R}^2$, $u\in W^{2,2}(\Omega)$, where $\Omega$ is a disk of radius $1/2$ centered at the origin. Let \[u(x,y) = \frac{x-y}{\sqrt{-\ln(x^2+y^2)}}\]
Using only the Laplacian for computing the 2-seminorm we have
\[\|u\|^2_{W^{2,2}(\Omega)} = \|u\|^2_{L^2(\Omega)} + \|\nabla u\|^2_{L^2(\Omega)} + \|\Delta u\|^2_{L^2(\Omega)}<\infty\]
But
\[
\frac{\partial u}{\partial x} = -\frac{x (x-y)}{(x^2+y^2) \sqrt{-\ln(x^2+y^2)}} + \frac{1}{ \sqrt{-\ln(x^2+y^2)}}
\]
goes to infinity near the origin. Thus the H\"older norm goes to infinity as Sobolev norm is finite.
So we present our proof of the General Sobolev inequality as follows:
Proof:
-
If $kp<n$
The sketch is that
\[W^{k,p}(\Omega)\hookrightarrow W^{k-1,p_1}\hookrightarrow W^{k-2,p_2}\hookrightarrow \cdots\hookrightarrow W^{0,p_k} \hookrightarrow L^{p_k}(\Omega)\]
where $\frac{1}{p_i}=\frac{1}{p}-\frac{i}{n}$This is true because we have the Gagliardo-Nirenberg-Sobolev inequality. Note that the immediate fact:
\[\|D^{\beta}u\|_{L^{p_1}(\Omega)}\le C\|D^{\alpha}u\|_{L^p(\Omega)}\le C\|u\|_{W^{k,p}(\Omega)}\]
where $|\alpha|=k,|\beta|=k-1$.Thus $u\in W^{k-1,p_1}$. By the similar estimation, we know the chain shown before. -
If $kp>n$ and $\frac{n}{p}$ is not an integer,
By the result in the first part, we know that for $m=\lfloor k-\frac{n}{p}\rfloor,r=k-\frac{n}{p}-m$, we have
\[W^{k,p}(\Omega)\hookrightarrow W^{m+1,q}\]
where $\frac{1}{q}=\frac{1}{p}-\frac{k-(m+1)}{n}$, an immediate result is that
\[\frac{1}{q}-\frac{1}{n}=\frac{1}{p}-\frac{k-m}{n}=\frac{1}{np}(n-p(k-m))<0\]
The Morrey's inequality yields:
\[W^{1,q}(\Omega)\hookrightarrow C^{0,\gamma}(\bar{\Omega})\]
where $\gamma=1-\frac{n}{q}=k-m-\frac{n}{p}$, and by the definition of the norms we can easily get that
\[W^{m+1,q}(\Omega)\hookrightarrow C^{m,\gamma}(\bar{\Omega})\] and we get the final result:
\[W^{k,p}(\Omega)\hookrightarrow W^{m+1,q}\hookrightarrow C^{m,\gamma}(\bar{\Omega})=C^{\lfloor k-\frac{n}{p}\rfloor,\lfloor \frac{n}{p}\rfloor+1-\frac{n}{p}}(\bar{\Omega})\] -
If $kp>n$ and $k-\frac{n}{p}=m$ is an integer, by similar proof before, we know
\[W^{k,p}(\Omega)\hookrightarrow W^{m+1,q}(\Omega)\]
where $\frac{1}{q}=\frac{1}{n}$. By Gagliardo-Nirenberg-Sobolev inequality, we know that $D^{\alpha}u\in L^r(\Omega)$ for all $n\le r<\infty$ and all $|\alpha|\le m$. Therefore, by Morrey's inequality, we know $D^{\alpha}u \in C^{0,1-\frac{n}{q}}$ for all $n<q<\infty$ and $|\alpha|\le m-1$. Thus we have
\[W^{k,p}(\Omega)\hookrightarrow W^{m+1,q}(\Omega)\hookrightarrow C^{m-1,\gamma}(\bar{\Omega})\]
holds for all $0<\gamma<1$.$\square$
3.5 Compact Embedding
We can now show the compact embedding of Sobolev space, as a general consequence of what we have observed before. We should give the definition first:
Definition 8.$X$ and $Y$ are Banach Spaces, $X\subset Y$. We say that $X$ is compactly embedded into $Y$, say $X\hookrightarrow\hookrightarrow Y$, is
- $X\hookrightarrow Y$
- Every bounded sequence in $X$ there is a converging subsequence in $Y$.
We may finally present the core of the Sobolev space here, say the compact embedding theorem:
Theorem 13.Assume $\Omega$ is a bounded open subset of $\mathbb{R}^n$, $\partial \Omega$ is $C^1$. Suppose $1\le p<n$, then
\[W^{1,p}(\Omega)\hookrightarrow\hookrightarrow L^q(\Omega)\]
for $1>\frac{1}{q}>\frac{1}{p}-\frac{1}{n}$.
To prove the theorem , first note that we have already proven that
\[W^{1,p}(\Omega)\hookrightarrow L^q(\Omega)\]
What we needs is the pre-compactness. We can use Azeala-Ascoli theorem here to come to the result. What we needs to find is the uniform bounded and equi-continuous property of each bounded array.
Proof:
-
If $\{u_m\}_{m=1}^{\infty}$ is a bounded sequence in $W^{1,p}(\Omega)$, what we should find is a subsequence $\{u_{m_j}\}_{j=1}^{\infty}$ that converges in $L^q(\Omega)$. First, WLOG, by extension theorem, we may assume that $\Omega=\mathbb{R}^n$ and $u_m$ has compact support within a bounded open set. By $\{u_{m_j}\}_{j=1}^{\infty}$ is bounded we say that
\[\sup\|u_m\|_{W^{1,p}(V)}< \infty\] -
We reuse $u_{m}^{\epsilon}=\rho_{\epsilon}\star u_m$, whereas $\rho_{\epsilon}$ is the mollifier we have defined before, to approximate the original sequence. And we get the core estimate
\[\|u^{\epsilon}(x)-u(x)\|_{L^1(\Omega)}\le \epsilon C\|\nabla u\|_{L^1(\Omega)}\]
The purpose of this estimation is to show that $u_m^{\epsilon}(x)\to u_m(x)$ uniformly. -
To prove the former statement, first note that
\[u^{\epsilon}(x)-u(x)=\int_{B(0,1)}(u(x-\epsilon y)-u(x))\rho(y)dy=-\epsilon\int_{B(0,1)}\left(\int_{0}^1\nabla u(x-\epsilon t y)\cdot ydt\right) dy\]
Thus
\begin{align*}\int_{\mathbb{R}^n}|u^{\epsilon}(x)-u(x)|dx &\le \epsilon\int_{\mathbb{R}^n}dx\left(\int_{B(0,1)}\left(\int_{0}^1\nabla u(x-\epsilon t y)\cdot ydt\right) dy\right) \\
&\le \epsilon \int_{B(0,1)} dy\int_{0}^1 ds\left(\int_{\mathbb{R}^n}|\nabla|(x)dx\right) \le C_n \epsilon \|\nabla u\|_{L^1}\le C \epsilon \|\nabla u\|_{L^p}
\end{align*}
We can also prove the theorem that
\[\|u^{\epsilon_j}-u^{\epsilon_l}\|_{L^1}\le CM(\epsilon_j+\epsilon_l)\]
This is proven by \textcolor{blue}{Homework} 9.So it's obvious that $u_m^{\epsilon}\to u_m$ uniformly
-
We should also note that By interpolation inequality with $1\le q<p^*$ that
\[\|u^{\epsilon}-u\|_{L^q(\Omega)}\le \|u^{\epsilon}-u\|_{L^1(\Omega)}^{\theta}\|u^{\epsilon}-u\|_{L^{p^*}(\Omega)}^{1-\theta}\]
where $\frac{1}{q}=\theta+\frac{1-\theta}{p^*}$, so by GNS inequality we have
\[\|u^{\epsilon}-u\|_{L^q(\Omega)}\le \|u^{\epsilon}-u\|_{L^1(\Omega)}^{\theta}\] -
Hence we now claim that for fixed $\epsilon$, sequence $\{u_m^{\epsilon}\}_{m=1}^{\infty}$ is uniformly bounded and equi-continuous. Since
\[|u_{n}^{\epsilon}(x)|\le \frac{1}{\epsilon^n}\int_{\mathbb{R}^n}|u(x-y)|\rho\left(\frac{y}{\epsilon}\right)dy\le \frac{C}{\epsilon^n}\|u\|_{L^1}\]
Also
\[|\nabla u_{n}^{\epsilon}(x)|=\frac{1}{\epsilon^n}\int_{\mathbb{R}^n}|u(y)|(\nabla\rho)\left(\frac{x-y}{\epsilon}\right)dy\le \frac{C}{\epsilon^{n+1}}\|u\|_{L^1}\]
where $C=\max(\nabla \rho)$From these two statements, we know that there exists subsequence $\{u_{n_k^i}^{\epsilon}\}$ is uniform bounded and equi-continuous for a fixed $\epsilon$, so we let $\epsilon_n=\frac{1}{2^n}$. And we choose the diangonal ones, that is
$\{u_{n_{l}^l}^{\epsilon_l}\}_{n=1}^{\infty}$(simplified as $u^{\epsilon_{l}}$) And we obtain
\[\|u^{\epsilon_{l_1}}-u^{\epsilon_{l_2}}\|_{L^q(\Omega)}\le\|u^{\epsilon_{l_1}}-u^{\epsilon_{l_2}}\|_{L^1(\Omega)}^{\theta}\le \left(CM\left(\frac{1}{2^{l_1}}+\frac{1}{2^{l_2}}\right)\right)^{\theta}\]
So the sequence is a Cauchy sequence in $L^q(\Omega)$. We may assume it converges to $\bar{u}$ -
We now claim that $\{u_{n_l}\}_{l=1}^{\infty}$ converges to $\bar{u}$. This is because
\[\|u_{n_l}-\bar{u}\|_{L^q(\Omega)}\le\|u_{n_l}-u^{\epsilon_l}\|_{L^q(\Omega)}+\|u^{\epsilon_l}-\bar{u}\|_{L^q(\Omega)}\]
The former and latter one all converges to zero. So the theorem is proven.$\square$





 浙公网安备 33010602011771号
浙公网安备 33010602011771号