$\newcommand\Im{\operatorname{Im}}$
$\newcommand\Ker{\operatorname{Ker}}$
$\newcommand\grad{\operatorname{grad}}$
$\newcommand\div{\operatorname{div}}$
$\newcommand\rot{\operatorname{rot}}$
$\newcommand\R{\mathbb{R}}$
本文主要来自于 Ib H. Madsen,Jxrgen Tornehave《从微积分到上同调》
故事要从牛顿-莱布尼兹公式说起。
(微积分基本定理)若$f(x)$是定义在开区间$(a,b)$上的连续函数$\Rightarrow$存在$F$,使得$F'=f$.
这个定理是现代微积分的基石。但是由于这个定理只描述了一元函数的情况,人们自然想“是否能把它推广到二元函数”?比如说,给定了一个函数$f=(f_1,f_2):U\to \mathbb{R}^2$,为定义在$\mathbb{R}^2$上开集$U$的光滑函数,那是否存在$F:U\to\mathbb{R}$,使得$\nabla F=f$?
也就是说,是否$\exists F$,使得\[\frac{\partial f_1}{\partial x_2}=\frac{\partial}{\partial x_2}\left(\frac{\partial F}{\partial x_1}\right)=\frac{\partial}{\partial x_1}\left(\frac{\partial F}{\partial x_2}\right)=\frac{\partial f_2}{\partial x_1}\]
(PS:这也给出了一个$F$存在的必要条件,也就是需要$\frac{\partial f_1}{\partial x_2}=\frac{\partial f_2}{\partial x_1}$)
但是满足了必要条件却不一定存在这样的$F$,书中就给出了这样一个经典的例子:
例子1 $U=\mathbb{R}^2\backslash \{0\},f:U\to\mathbb{R}^2, (x_1,x_2)\mapsto (\frac{-x_2}{x_1^2+x_2^2},\frac{x_1}{x_1^2+x_2^2})$
我们认为,不存在$F:U\to\mathbb{R}^2$,使得$\frac{\partial F}{\partial x_1}=f_1,\frac{\partial F}{\partial x_2}=f_2$. 否则的话就有
\[\frac{d}{d\theta}F(\cos{\theta},\sin{\theta})=\frac{\partial F}{\partial x_1}(\cos{\theta},\sin{\theta})(-\sin{\theta})+\frac{\partial F}{\partial x_2}(\cos{\theta},\sin{\theta})(\cos{\theta})=1\]
但是另外又有\[\int_{0}^{2\pi}\frac{d}{d\theta}F(\cos{\theta},\sin{\theta})d\theta=F(\cos{\theta},\sin{\theta})|_{0}^{2\pi}=0\]
矛盾!
例子2 $U=\{(x_1,x_2)\in\mathbb{R}^2|x_1^2+x_2^2<1\}$为开集,则$f:U\to\mathbb{R}^2,(x_1,x_2)\mapsto (x_1^2+x_2,x_1)$有“原函数” $F(x_1,x_2)=\frac{1}{3}x^3+x_1x_2$
为什么这个函数存在所谓的“原函数”呢?其实这和区域的性质有关,实际上,定义在这个单位圆盘上满足必要条件的函数都有“原函数”。更推广地我们可以刻画这个区域,也即“星形区域”(Star-shaped).
定义 $U\in\mathbb{R}^2$为开集,$U$被称为关于$x_0$的星形区域,如果对于$\forall x\in U$,线段$\overline{x_0 x}\subset U$.
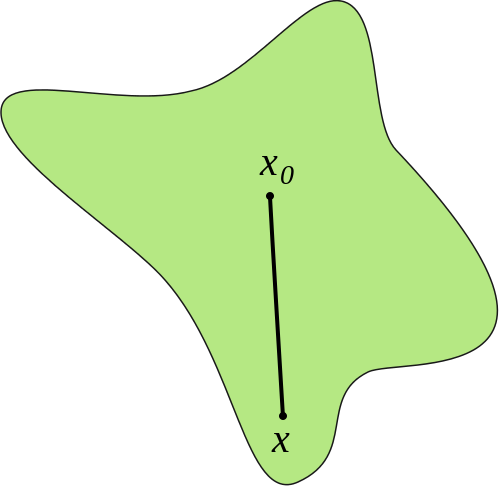
如图就是一个星形区域。而例1中的区域并非星形的,因为任意$x_0$,它关于原点的对称点不能连线段在区域内。
星形区域有什么好的性质呢?正如前面所说,在这个区域内,就有$\frac{\partial f_1}{\partial x_2}=\frac{\partial f_2}{\partial x_1}$与存在原函数$F$等价!具体定理叙述如下:
定理1 $U\in\mathbb{R}^2$是开的星形区域,且$f:U\to\mathbb{R}^2$光滑(实际上只要可导似乎就行了),$f=(f_1,f_2)$.且$\frac{\partial f_1}{\partial x_2}=\frac{\partial f_2}{\partial x_1}$,那么$\exists F:U\to\mathbb{R}$ 光滑,且有$\frac{\partial F}{\partial x_1}=f_1,\frac{\partial F}{\partial x_2}=f_2$.
WLOG,我们可设$U$关于$x_0=0\in \mathbb{R}^2$是星形的。令
\[F(x_1,x_2)=\int_{0}^{1}(x_1 f_1(tx_1,tx_2)+x_2 f_2(tx_1,tx_2))dt\]
那么计算$\frac{\partial}{\partial x_1}F(x_1,x_2)$,可以得到
\[\begin{align*}\frac{\partial}{\partial x_1}F(x_1,x_2)&=\int_0^1 [f_1(tx_1,tx_2)+tx_1\frac{\partial f_1}{\partial x_1}(tx_1,tx_2)+tx_2\frac{\partial f_2}{\partial x_1}(tx_1,tx_2)]dt\\ &= \int_{0}^1\frac{d}{dt}(tf(tx_1,tx_2))=f_1(x_1,x_2)\end{align*}\]
同理亦可得另一边的等式。$\square$
为什么星形区域有两者等价,而去掉一点的区域却不行呢?我们再用场论的符号来叙述下以上的事实。
$U\in\mathbb{R}^2$,我们要研究的是$C^{\infty}(U,\mathbb{R}^k)=\{\mbox{smooth function on }U\}$,这个可看成一个线性空间。
我们定义符号$\grad:C^{\infty}(U,\mathbb{R})\to C^{\infty}(U,\mathbb{R}^2)$,使得$\grad(f)=(\frac{\partial f_1}{\partial x_1},\frac{\partial f_2}{\partial x_2})$
以及$\rot:C^{\infty}(U,\mathbb{R}^2)\to C^{\infty}(U,\mathbb{R})$,使得$\rot((f_1,f_2))=\frac{\partial f_1}{\partial x_2}-\frac{\partial f_2}{\partial x_1}$
则我们可以给出如下的链:
$$\require{AMScd}
\begin{CD}
C^{\infty}(U,\mathbb{R}) @>{\grad}>> C^{\infty}(U,\mathbb{R}^2) @>{\rot}>> C^{\infty}(U,\mathbb{R})
\end{CD}$$
有两条性质
- $\rot\circ\grad = 0$(由于导数可交换)
- $\Im(\grad)\in\Ker(\rot)$(由1立刻得到)
为了刻画这两者之间的包涵关系,我们定义
$$H^1(U):=\frac{\Ker(\rot)}{\Im(\grad)}={\alpha+\Im(\grad)}$$
这样一个商群就是所谓的第一上同调群,代表元$[\alpha]=[\beta]\Leftrightarrow \alpha-\beta\in\Im(\grad)$,值得一提的是$H^1(U)$通常是有限维的。
前面的定理1让我们知道,对于开星形区域$U$,就有$\Ker(\rot)\in\Im(\grad)$,从而$H^1(U)$中只有$0$元(这也是定理1的重述)。而从例子1我们知道,对于$U=\mathbb{R}^2\backslash\{(0,0)\}$,$H^1(U)\not = 0$.
同样我们可以定义第0上同调群,也就是$H^0(U)=\Ker(\grad)$
我们同样可以计算某些区域的第0上同调群,定理如下:
定理2 $U$为$\mathbb{R}^2$中连通开集,那么有$H^0(U)=\mathbb{R}$
这个证明也很显然,因为$f$总在一个局部为常数,而且集合连通,使$f$为常数的区域既开又闭,从而在整个区域上都为常数。
考虑完二维的情况,我们同样可以考虑三维的情况,这时候有这样一个链
$$\begin{CD}
C^{\infty}(U,\mathbb{R}) @>{\grad}>> C^{\infty}(U,\mathbb{R}^3) @>{\rot}>> C^{\infty}(U,\mathbb{R}^3)@>{\div}>> C^{\infty}(U,\mathbb{R})
\end{CD}$$
这三个东西的定义经过计算同样有 $\rot\circ\grad=0,\div\circ\rot=0$
所以类似地我们定义几个上同调群,即
$$H^0(U)=\Ker(\grad),H^1(U)=\frac{\Ker(\rot)}{\Im(\grad)},H^2(U)=\frac{\Ker(\div)}{\Im(\rot)}$$
(读到这想必也发现了,同调与上同调无非就是两个算子$\partial_1\circ\partial_2=0$定义出的群$\Ker(\partial_1)/\Im(\partial_2)$而已,没什么高深的知识,不过在拓扑中却非常有用)
定理3 在$\mathbb{R}^3$中的开星形区域$U$,有$H^0(U)=\mathbb{R},H^1(U)=0,H^2(U)=0$
前两个同调用前面的方法即可,我们需要算的是$H^2(U)=0$,只需要对于$\forall F\in\Ker(\div)$,找到$G$使得$\rot(G)=F$。而显然
\[G(\vec{x})=\int_0^1(F(t\vec{x})\times(t\vec{x}))dt\]
满足条件。
同样我们也举出例子,让$H^1(U)\not = 0$.
例3 $S=\{(x_1,x_2,x_3)\in\mathbb{R}^3,x_1^2+x_2^2=1,x_3=0\}$,而区域$U=\mathbb{R}^3\backslash S$,则令$$f(x_1,x_2,x_3)=\left(\frac{-x_1x_3}{x_3^2+(x_1^2+x_2^2-1)^2},\frac{-x_2x_3}{x_3^2+(x_1^2+x_2^2-1)^2},\frac{x_1^2+x_2^2-1}{x_3^2+(x_1^2+x_2^2-1)^2}\right)$$
我们声称$\rot(f)=0$,即$[f]\in H^1(U)$但是$H^1(U)\not = 0$,否则若$\exists F\in C^{\infty}(U,\mathbb{R})$,使得$\grad{F}=f$
那么考虑曲线$\gamma(t)=(\sqrt{1+\cos{t}},0,\sin{t}),-\pi\le t\le \pi$,则有$\frac{d}{dt}F(\gamma(t))=1,\int_{-\pi}^{\pi}\frac{d}{dt}F(\gamma(t))dt=0$.
从上我们可以大致有这样一点想法:如果$H^1(U)\not = 0$,那就有个$1$维的“洞”,那么是不是$H^2(U)\not =0$就表明有$2$为的洞了呢?这个博主还不是很明白,需要继续学习,来补充这篇文章。



