GCM

GaloisCounter Mode (GCM)

运算符与函数

$0^s$	包含了$s$个$0$的比特串。
$\mbox{CIPH}_K⁡(X)$	在密钥$K$下对分组$X$应用分组密码得到的输出。
$\mbox{GCTR}_K⁡(ICB,X)$	在密钥K下对包含初始组计数$ICB$的比特串X应用包含给定分组加密的 $\mbox{GCTR}$函数的输出。
$\mbox{GHASH}_H⁡(X)$	在hash子密钥H下对比特串X应用$\mbox{GHASH}$函数的输出。
$\mbox{inc}_s⁡(X)$	比特串X的最右$s$个比特自增并模$2^s$后表示为二进制形式的输出。
$int⁡(X)$	二进制比特串$X$对应的整数。
$\mbox{len}⁡(X)$	比特串$X$的比特长度。
$\mbox{LSB}_s⁡(X)$	比特串$X$的最右$s$个比特组成的比特串。
$\mbox{MSB}_s⁡(X)$	比特串$X$的最左$s$个比特组成的比特串。
$⌈x⌉$	不小于实数$x$的最小整数。
$[x]_s$	非负整数$x$表示为$s$比特的二进制字符串，其中$x<2^s$。
$X≫1$	弃置比特串$X$的最右比特并在左侧增加$0$比特而产生的比特串。
$X∥Y$	两个比特串$X$和$Y$的级联。
$X⊕Y$	两个相同长度比特串$X$和$Y$按比特进行异或运算。
$X•Y$	两个分组$X$和$Y$的积，视作二进制伽罗瓦域的元素。
$X^i$	$X$在“$•$”乘法的$i$次幂，其中$i$为正整数。
$x⋅y$	两个整数$x$和$y$的积。

GCM的算数组件
递增函数
对于满足\(\mbox{len}(X)≥s\)的正整数\(s\)与比特串\(X\)，记\(\mbox{inc}_s⁡(X)\)为\(s\)-bit的递增函数，定义如下：

$\mbox{inc}_s⁡(X)=\mbox{MSB}_{\mbox{len}(X)-s}⁡(X)∥[\mbox{int⁡}(\mbox{LSB}_s⁡(X) )+1 \mbox{ mod } 2^s]_s$

分组倍乘运算符
令\(R\)为比特串\(11100001∥0^{120}\)。对于给定的两个分组\(X\)和\(Y\)，如下的Algorithm计算分组的“积”，记为\(X•Y\)：
Algorithm：\(X•Y\)
输入：
  分组\(X\)，\(Y\)。
输出：
  分组\(X•Y\)。
步骤：

1. 记\(x_0x_1…x_{127}\)为\(X\)的比特序列。
2. 令\(Z_0=0^{128}\)与\(V_0=Y\)。
3. 对于\(i=0\)到\(127\)，以如下方式计算分组\(Z_{i+1}和V_{i+1}\)：\( Z_{i + 1} = \begin{cases} Z_{i} & {\text{if}~x_{i} = 0} \\ {Z_{i} \oplus V_{i}} & {\text{if}~x_{i} = 1} \end{cases}\)\(V_{i + 1} = \begin{cases} {V_{i} \gg 1} & {\text{if}~{{\text{L}\text{SB}}_{1}\left( V_{i} \right)} = 0} \\ {\left( {V_{i} \gg 1} \right) \oplus R} & {\text{if}~{{\text{L}\text{SB}}_{1}\left( V_{i} \right)} = 1} \end{cases}\)
4. 返回\(Z_{128}\)。

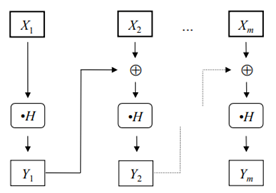
\(\mbox{GHASH}\)函数
Algorithm：\(\mbox{GHASH}_H⁡(X)\)
预准备：
  分组\(H\)，hash子密钥。
输入：
  满足\(\mbox{len}⁡(X)=128m\)的比特串\(X\)，其中\(m\)为正整数。
输出：
  分组\(\mbox{GHASH}_H⁡(X)\)。
步骤：

1. 记\(X_1,X_2,…,X_{m-1},X_m\)为满足\(X=X_1∥X_2∥⋯∥X_{m-1}∥X_m\)的唯一组序列。
2. 令\(Y_0\)为“零组”，即\(0^{128}\)。
3. 对于\(i=1\)到\(m\)，计算\(Y_i=(Y_{i+1}⊕X_i )•H\)。
4. 返回\(Y_m\)。

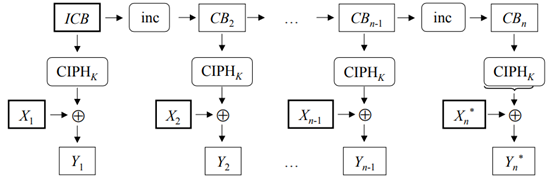
\(\mbox{GCTR}\)函数
Algorithm：\(\mbox{GCTR}_K⁡(ICB,X)\)
预准备：
  长度为128-bit的分组密码\(\mbox{CIPH}\)；
  密钥\(K\)。
输入：
  初始组计数\(ICB\)；
  任意长度比特串\(X\)。
输出：
  长度为\(\mbox{len}⁡(X)\)的比特串\(Y\)。
步骤：

1. 若\(X\)为空串，则返回为空串的\(Y\)。
2. 令\(n=\mbox{len}⁡(X)⁄128\)。
3. 记\(X_1,X_2,…,X_{n-1},X_n^*\)为满足\(X=X_1∥X_2∥⋯∥X_{n-1}∥X_n^*\)的唯一比特串序列，其中\(X_1,X_2,…,X_{n-1}\)为完整的组。
4. 令\({CB}_1=ICB\)。
5. 对于\(i=2\)到\(n\)，计算\({CB}_i=\mbox{inc}_{32}⁡({CB}_{i-1})\)。
6. 对于\(i=1\)到\(n-1\)，计算\(Y_i=X_i⊕\mbox{CIPH}_K⁡({CB}_i)\)。
7. 计算\(Y_n^*=X_n^*⊕\mbox{MSB}_{\mbox{len} ⁡(X_n^*)}⁡(\mbox{CIPH}_K⁡({CB}_n ) )\)。
8. 令\(Y=Y_1∥Y_2∥⋯∥Y_{n-1}∥Y_n^*\)。
9. 返回\(Y\)。

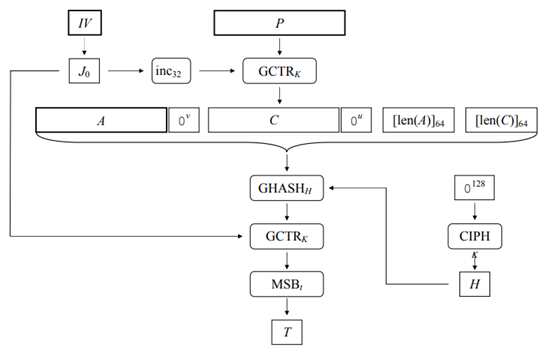
认证加密函数的算法(Algorithm for the Authenticated Encryption Function)

Algorithm: \(\mbox{GCM-AE}_K⁡(IV,P,A)\)
预准备：
  长度为128-bit的分组密码\(\mbox{CIPH}\)；
  密钥\(K\)；
  定义支持的输入-输出长度；
  支持的key相关标签长度\(t\)。
输入：
  初始化向量\(IV\)；
  明文\(P\)；
  额外认证数据\(A\)。
输出：
  密文\(C\)；
  认证标签\(T\)。
步骤：

1. 令\(H=\mbox{CIPH}_K⁡(0^{128})\)。
2. 定义如下的分组\(J_0\)：
   若\(\mbox{len}⁡(IV)=96\)，则令\(J_0=IV∥0^{31}∥1\)。
   若\(\mbox{len}⁡(IV)≠96\)，则令\(s=128⌈\mbox{len}(IV)⁄128⌉-\mbox{len}⁡(IV)\)，且令\(J_0=\mbox{GHASH}_H⁡(IV∥0^{s+64}∥[\mbox{len}⁡(IV) ]_{64})\)。
3. 计算\(C=\mbox{GCTR}_H⁡(\mbox{inc}_{32}⁡(J_0 ),P)\)。
4. 计算\(u=128⋅⌈\mbox{inc}⁡(C)⁄128⌉-\mbox{len}⁡(C)\)且令\(v=128⋅⌈\mbox{len}⁡(A)⁄128⌉-\mbox{len}⁡(A)\)。
5. 定义如下的分组\(S\)：\(S=\mbox{GHASH}_H⁡(A∥0^v∥C∥0^u∥[\mbox{len}⁡(A)]_{64}∥[\mbox{len}⁡(C)]_{64})\)
6. 计算\(T=\mbox{MSB}_t⁡(\mbox{GCTR}_K⁡(J_0,S) )\)。
7. 返回\((C,T)\)。

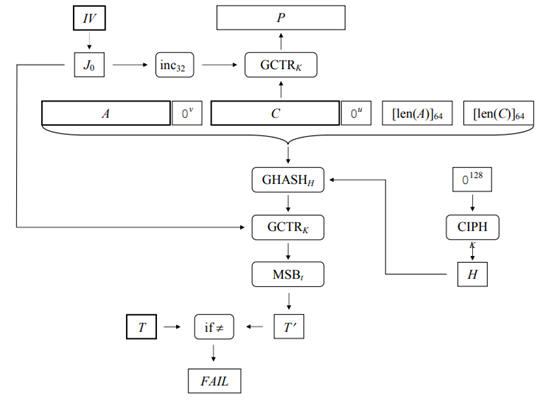
认证解密函数的算法(Algorithm for the Authenticated Decryption Function)

Algorithm:\(\mbox{GCM-AD}_K⁡(IV,C,A,T)\)
预准备：
  长度为128-bit的分组密码\(\mbox{CIPH}\)；
  密钥\(K\)；
  定义支持的输入-输出长度；
  支持的key相关标签长度\(t\)。
输入：
  初始化向量\(IV\)；
  密文\(C\)；
  额外认证数据\(A\)；
  认证标签\(T\)。
输出：
  明文\(P\)或非可信标识\(FAIL\)。
步骤：

1. 若\(IV\)，\(A\)或\(C\)的长度不支持，或\(\mbox{len}⁡(T)≠t\)，则返回\(FAIL\)。
2. 令\(H=\mbox{CIPH}_K⁡(0^{128})\)。
3. 定义如下的分组\(J_0\)：
   若\(\mbox{len}(IV)=96\)，则令\(J_0=IV∥0^{31}∥1\)。
   若\(\mbox{len}⁡(IV)≠96\)，则令\(s=128⌈\mbox{len}(IV)⁄128⌉-\mbox{len}⁡(IV)\)，且令\(J_0=\mbox{GHASH}_H⁡(IV∥0^{s+64}∥[\mbox{len}⁡(IV) ]_{64})\)。
4. 令\(P=\mbox{GCTR}_K⁡(\mbox{inc}_{32}⁡(J_0 ),C)\)。
5. 令\(u=128⋅⌈\mbox{len}⁡(C)⁄128⌉-\mbox{len}⁡(C)\)且令\(v=128⋅⌈\mbox{len}⁡(A)⁄128⌉-\mbox{len}⁡(A)\)。
6. 定义如下的分组\(S\)：
   \(S=\mbox{GHASH}_H⁡(A∥0^v∥C∥0^u∥[\mbox{len}⁡(A)]_{64}∥[\mbox{len}⁡(C)]_{64})\)
7. 计算\(T'=\mbox{MSB}_t⁡(\mbox{GCTR}_K⁡(J_0,S))\)。
8. 若\(T=T'\)，则返回\(P\)，否则返回\(FAIL\)。

参考
NIST-SP-800-38D Recommendation for Block Cipher Modes of Operation GaloisCounter Mode (GCM) and GMAC