Montgomery Curves and Weierstrass Curves

Weierstrass Curves
Weierstrass Curves形如

$y^2=x^3+Ax+B$
其中$4A^3+27B^2\ne 0$，这种形式称为Weierstrass Form。

Weierstrass Curves上的运算
在椭圆曲线(此处即为Weierstrass Curves)上，可以定义点之间的加法运算，其满足：

1. 单位元$O$为无穷远点
2. 对于曲线上的两点$P$和$Q$，取经过$P$和$Q$的直线，这条直线与椭圆曲线相较于最多三个点，其中两个点是$P$和$Q$，如果第三个点存在且不与$P$和$Q$重合，记第三个点为$-R$，那么满足$P+Q-R=O$，即$P+Q=R$。
3. 对一点$R=(x_3,y_3)$，其加法逆元$-R=(x_3,-y_3)$，也即点$R$沿$x$轴的对称点。

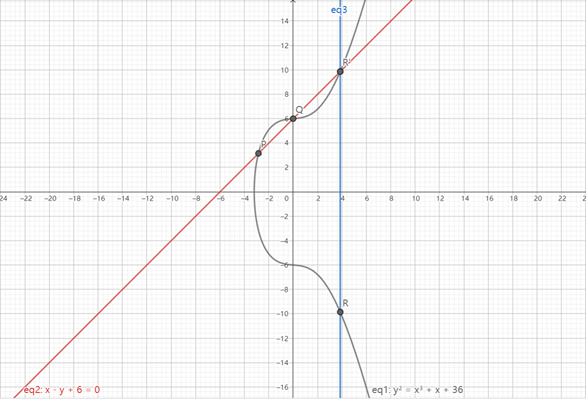
那么，对于Weierstrass Curves在有限域上的运算便有：

1. 有限域的加法逆元
   $P(x,y)$的加法逆元是$(x,-y(\mathrm{mod}p))=(x,p-y)$
2. 斜率的计算分为两种情况，分别为$P=Q$(也即$P$和$Q$为曲线上的切点)和$P\ne Q$，计算过程如下：$k=\{\begin{array}{cc}\frac{3x_1^2+a}{2y_1}& P=Q\\ \frac{y_2-y_1}{x_2-x_1}& P\ne Q\end{array}$
3. 有限域的加法
   $P(x_1,y_1)，Q(x_2,y_2)\mathrm{和}R(x_3,y_3)$三点（其中$R$是直线$PQ$与曲线交点关于$x$轴的对称点，即有$R=P+Q$）有如下关系：$\{\begin{array}{l}{x}_3\equiv k^2-x_1-x_2\left(\text{mod}p\right)\\ y_3\equiv k\left(x_1-x_3\right)-y_1\left(\text{mod}p\right)\end{array}$
   
   
   

Weierstrass Curves上的基点运算
下面以曲线

$y^2\equiv x^3+2x+1(\mathrm{mod}13)$ 在模$13$运算下为例，也即$A=2$，$B=1$，$p=13$，${\mathbb{F}}_p={\mathbb{F}}_{13}$。选取基点(base point)$G=(8,3)$，不妨可以验证基点$G$是否在曲线之上。通过计算有 $y^2=3^2\equiv 9(\mathrm{mod}13)=529=8^3+2\cdot 8+1=x^3+2x+1$ 可见选取的基点$G$位于曲线之上。

1.$2G$的计算
下面首先进行$2G$的计算，对于这种形如$2^{k}G$的运算可以认为是$P=Q=2^{\frac{k}{2}}G$的情况进行计算。对于此处，即有$P=Q=(8,3)$对应上节所述的切点情况，计算过程如下：

$k\equiv \frac{3\cdot 8^2+3}{2\cdot 3}(\mathrm{mod}13)\equiv 12\cdot 6^{-1}(\mathrm{mod}13)\equiv 12\cdot 11(\mathrm{mod}13)\equiv 2(\mathrm{mod}13)$ $x\equiv 2^2-8-8(\mathrm{mod}13)\equiv -12(\mathrm{mod}13)\equiv 1(\mathrm{mod}13)$ $y\equiv 2(8-1)-3(\mathrm{mod}13)\equiv 11(\mathrm{mod}13)$ 如此计算获得了$2G$对应的点坐标为$2G=(1,11)$。

2.$3G$的计算
对于$3G$的计算，可以认为$P=2G=(1,11)$，$Q=G=(8,3)$，$3G=P+G$，也即上节所述的非切点的情况，计算过程如下：

$k\equiv \frac{3-11}{8-1}(\mathrm{mod}13)\equiv -8\cdot 7^{-1}(\mathrm{mod}13)\equiv 5\cdot 2(\mathrm{mod}13)\equiv 10(\mathrm{mod}13)$ $x\equiv {10}^2-8-1(\mathrm{mod}13)\equiv 91(\mathrm{mod}13)\equiv 0(\mathrm{mod}13)$ $y\equiv 10(1-0)-11(\mathrm{mod}13)\equiv -1(\mathrm{mod}13)\equiv 12(\mathrm{mod}13)$ 如此计算获得了$3G$对应的点坐标为$3G=(0,12)$。

通过类似与上述过程的运算，可以依次获得$4G=(2,0)$，$5G=(0,1)$，$6G=(1,2)$，$7G=(8,10)$。在计算$8G$时，若是通过$P=Q=4G$的方式进行计算会发现$4G$的$y$为$0$，从而导致$k$指向无穷大，亦或是通过$P=7G$，$Q=G$的方式进行计算会发现$G$和$7G$具有相同的$x$，同样导致$k$指向无穷大。
事实上，此处有$8G=O$，也即$8G$对应了椭圆曲线的无穷远点(类似于整数中的$0$)。对于无穷远点，同样可以进行加法运算，如对$P=O$，$Q=G$进行加法有

$P+Q=O+G=G$ 此外，对于椭圆曲线而言其存在阶(Order)的概念。如上述的曲线，因$9G=8G+G=O+G=G\Rightarrow 8G=0$，故对于基点$G=(8,3)$有$\text{ord}(G)=8$。阶的概念描述了椭圆曲线在有限域${\mathbb{F}}_p$中对于基点$G$生成元素的个数。需要注意，对于相同椭圆曲线的不同基点选择，可能对应了不同的阶，如对于基点$G=(1,2)$有$\text{ord}(G)=4$，读者可自行计算验证。

Montgomery curve
对于椭圆曲线而言，Montgomery curve形式同样是较为常用表达形式，具体如下：

$K{y}^2=x^3+J{x}^2+x$ 其中，$K(J^2-4)\ne 0$。 事实上，现阶段应用最为广泛的椭圆曲线之一——Curve25519，便是采用了这种形式的曲线，其具有如计算迅速等优点。对于Curve25519具有如下形式： $y^2\equiv x^3+486662x^2+x(\mathrm{mod}{2}^{255}-19)$

对于Montgomery curve，可以在一定条件下转换为Weierstrass Curves，转换过程可以通过如下过程：
1.消除等式左侧系数$K$
定义

$\{\begin{array}{l}u=\frac{x}{K}\\ v=\frac{y}{K}\end{array}$

带入Montgomery curve表达式$K{y}^2=x^3+J{x}^2+x$有

$K{\left(Kv\right)}^2={\left(Ku\right)}^3+J{\left(Ku\right)}^2+Ku$ $v^2=u^3+\frac{J}{K}{u}^2+\frac{1}{K^2}u$

2.消除等式右侧二次项
定义

$\{\begin{array}{l}u=a-\frac{J}{3K}\\ v=b\end{array}$

带入上述表达式有

$\begin{array}{ccc}{b}^2& =& {\left(a-\frac{J}{3K}\right)}^3+\frac{J}{K}{\left(a-\frac{J}{3K}\right)}^2+\frac{1}{K^2}\left(a-\frac{J}{3K}\right)\\ & =& \left(a^3-\frac{J}{K}{a}^2+\frac{J^2}{3K^2}a-\frac{J^3}{27K^3}\right)+\frac{J}{K}\left(a^2-\frac{2J}{3K}a+\frac{J^2}{9K^2}\right)+\frac{1}{K^2}\left(a-\frac{J}{3K}\right)\\ & =& a^3+\left(-\frac{J}{K}+\frac{J}{K}\right)a^2+\left(\frac{J^2}{3K^2}-\frac{2J^2}{3K^2}+\frac{1}{K^2}\right)a+\left(-\frac{J^3}{27K^3}+\frac{J^3}{9K^3}-\frac{J}{3K^3}\right)\\ & =& a^3+\frac{3-J^2}{3K^2}a+\frac{2J^3-9J}{27K^2}\end{array}$

此时，$(a,b)$即为Weierstrass Curves上的点。转换式为：

$\{\begin{array}{l}x=Ka-\frac{J}{3}\\ y=Kb\end{array},\{\begin{array}{l}A=\frac{3-J^2}{3K^2}\\ B=\frac{2J^3-9J}{27K^2}\end{array}$

例如，就上节所述的Weierstrass Curves

$b^2\equiv a^3+2a+1\left(\text{mod}13\right)$

转换为Montgomery curve有

$y^2\equiv x^3+6x^2+x\left(\text{mod}13\right)$ $\{\begin{array}{l}x\equiv a+11\left(\text{mod}13\right)\\ y\equiv b\left(\text{mod}13\right)\end{array}$

此外Montgomery curve同样可以转换为Twisted Edwards curve(形式如$a{x}^2+y^2=1+d{x}^2{y}^2$)，此处不再赘述。





参考
椭圆曲线 - 杰哥的知识库 (jia.je)
密码学[3]：椭圆曲线-腾讯云开发者社区-腾讯云 (tencent.com)