Logistic Regression
可以从线性回归推到logistic regression.
首先介绍线性回归。
线性回归是非常基础的模型,它的几个假设有:
(1)假设对x的测量数据没有误差
(2)假设y的期望是系数和x的线性组合
(3)假设误差独立同分布,分布为\(N(0,\sigma^2)\)
(4)假设变量x之间没有多重共线性(即设计矩阵列满秩。设计矩阵的列数为x变量数,行数为样本数)(如果变量x之间有多重共线性,那么,利用最小二乘法求解问题,将导致解不稳定。针对这一问题,可以利用脊回归解决)
对于样本\({(x_1,y_1),(x_2,y_2),......,(x_p,y_p)}\),线性回归的学习模型是$$f(x_i) = wx_i+b$$损失函数使用均方误差$$\sum_{i = 1}p(f(x_i)-y_i)2$$然后基于损失函数最小化求解参数w和b。
接下来先讲一下 logistic function
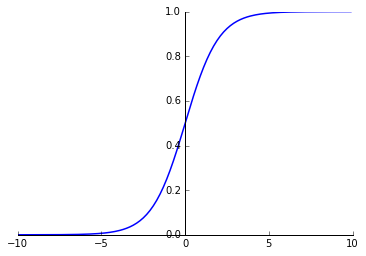
由于logistic function非常陡峭,如果将\(f(x_i)\)通过这个函数映射之后,结果要么接近于0,要么接近于1,所以可以据此进行二分类。
Logistic Regression
将\(z = wx+b\)与\(y = logistic(z)\)复合之后得到$$y = \frac{1}{1+e^{-(wx+b)}}$$变换一下得到$$ln\frac{y}{1-y} = wx+b$$
现在想求参数w和b。不妨记\(\beta = (w;b), \hat{x} = (x;1)\),那么$$ln\frac{y}{1-y} = \beta^T\hat{x}$$
如果将y看作x分成正例的可能性,1-y看作x被分到负例的概率,则\(\frac{y}{1-y}\)反映了x作为正例的相对可能性,称为“几率”。
接下来就可以利用“极大似然法”估计\(\beta\)了。
记$$p(y_i|x_i;w,b) = y_ip_1(\hat{x_i};\beta) + (1-y_i)p_0(\hat{x_i};\beta)$$
对数似然函数为$$l(w,b) = \sum_{i = 1}^plnp(y_i|x_i;w,b)$$
接下来$$\begin{eqnarray}l(w,b)
&=& \sum_{i = 1}^pln[y_ip_1(\hat{x};\beta)+(1-y_i)p_0(\hat{x};\beta)]\
&=& \sum_{i = 1}pln[y_i\frac{e{\betaT\hat{x_i}}}{1+e{\betaT\hat{x_i}}}+(1-y_i)\frac{1}{1+e{\beta^T \hat{x_i}}}]\ &=& \sum_{i = 1}pln[\frac{e{y_i\betaT\hat{x_i}}}{1+e{\beta\hat{x_i}}}]\
&=& \sum_{i = 1}p[y_i\betaT\hat{x_i}-ln(1+e^{\beta\hat{x_i}})]
\end{eqnarray}$$
最大化\(l(w,b)\) = 最小化\(-l(w,b)\),这就将求参数问题转换成了最优化问题求解。求解这种无约束的凸优化问题可以利用梯度下降法、牛顿法等。
Logistic Regression的优点
(1)直接对分类可能性进行建模,无需实现假设数据分布,避免因假设分布不准确所带来的问题。
(2)还可以得到近似概率预测,这对许多利用概率辅助决策的任务很重要。
(3)对率函数是任意阶可导的凸函数,有很好的数学性质,现有的许多数值优化算法都可以直接用于求取最优解。
例子
使用西瓜书中的西瓜数据,实现一下西瓜书中的Logistic Regression练手,但是感觉代码不优雅。。。贴出来接受指正。
`
python
import numpy as np
#使用的数据集
X = np.array([[0.697,0.460],
[0.774,0.376],
[0.634,0.264],
[0.608,0.318],
[0.556,0.215],
[0.403,0.237],
[0.481,0.149],
[0.437,0.221],
[0.666,0.091],
[0.243,0.267],
[0.245,0.057],
[0.343,0.099],
[0.639,0.161],
[0.657,0.198],
[0.360,0.370],
[0.593,0.042],
[0.719,0.103]])
Y = np.array([1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0])
class LogisticRegression():
def __init__(self,max_iter= 300,B = None,lable = None):
self.max_iter = max_iter
self.B = B
self.lable = lable
def fit(self,X,Y):
"""
X:训练数据,矩阵维度为:n_samples * n_features
Y:n_samples个类标
"""
self.lable = list(set(Y))
changeY = np.zeros(Y.shape[0])
k = 0
for i in self.lable:
changeY[np.where(Y == i)[0]] = k
k+=1
Y = changeY
X = np.asarray(X)
Y = np.asarray(Y)
if X.shape[1] == 0:
print('没有特征变量')
return 0
elif X.shape[0] == 0:
print('没有样本')
elif X.shape[0] != Y.shape[0]:
print('X与Y的样本量不同')
else:
B = self.main_function(X,Y)
self.B = B
return self
def main_function(self,X,Y):
"""
利用梯度下降求目标函数最优解
"""
#合并偏执项b
X = np.concatenate((X,np.ones((X.shape[0],1))),axis = 1)
#初始化系数变量
B = np.random.uniform(0,1,X.shape[1])
#优化的目标函数
X = np.mat(X)
BX = B*X.T
L = -(BX*np.mat(Y).T)+ np.sum(np.log(1+np.exp(BX)))
L_sub = L
aiter = 0
while aiter < self.max_iter:
aiter += 1
#判断
if L_sub<1e-10:
break
#更新B
B1 = np.zeros((X.shape[1]))
B2 = np.mat(np.zeros((X.shape[1],X.shape[1])))
for i in range(X.shape[0]):
p1 = np.exp(B*X[i,:].T)/(1+np.exp(B*X[i,:].T))
p1 = p1[0,0]
B1 = B1+(-X[i,:]*(Y[i]-p1))
B2 = B2+(X[i,:].T*X[i,:]*p1*(1-p1))
#更新B
B = B - B1*np.linalg.inv(B2)
BX = B*X.T
L_1 = L
L = -(BX*np.mat(Y).T)+ np.sum(np.log(1+np.exp(BX)))
L_sub = L_1-L
return B
def predict(self,X):
"""
给定数据集进行预测
"""
X = np.concatenate((X,np.ones((X.shape[0],1))),axis = 1)
X = np.mat(X)
labels = np.zeros((X.shape[0]))
ratio = []
for i in range(X.shape[0]):
BX = self.B*X[i].T
p1 = BX/(1+BX)
p2 = 1/(1+BX)
ratio.append(np.array(p1/p2).flatten()[0])
#分类阈值
if p1 > p2:
labels[i] = int(self.lable[1])
else:
labels[i] = int(self.lable[0])
return np.array(labels),ratio
def ROC(ratio,Y):
import operator
"""根据样本作为正例的可能性p1.和作为负例的可能性p0的比值ratio,
计算假正例率和正正例率"""
ratio_dict = {}
k = 0
for i in ratio:
ratio_dict[k] = i
k += 1
#排序
ratio_s = sorted(ratio_dict.items(),key = operator.itemgetter(1),
reverse = True)
Y_s = []
for i in ratio_s:
Y_s.append(Y[i[0]])
num_P = Y_s.count(1) #实际正例数 = (TP+FN)
num_F = Y_s.count(0) #实际反例数 = (TN+FP)
x_FPR = [] #假正例率 FPR = FP/(TN+FP)
y_TPR = [] #真正例率 TPR = TP/(TP+FN)
#计算真正例和假正例个数
count_FP = 0
count_TP = 0
for i in range(len(ratio)):
if Y_s[i] == 1: #真正例
count_TP += 1
else: #假正例
count_FP += 1
x_FPR.append(count_FP/num_F)
y_TPR.append(count_TP/num_P)
#AUC
area = 0
for i in range(len(ratio)-1):
area += (x_FPR[i+1] - x_FPR[i])*(y_TPR[i+1]+y_TPR[i])
AUC = area/2
#画图
import matplotlib.pyplot as plt
plt.figure()
plt.plot(x_FPR,y_TPR)
plt.title('ROC(AUC = %.2f)'%AUC)
plt.xlabel('FPR')
plt.ylabel('TPR')
`






