笛卡尔树（递归，二叉树）

题意

笛卡尔树是由一系列不同数字构成的二叉树。

树满足堆的性质，中序遍历返回原始序列。
最小笛卡尔树表示满足小根堆性质的笛卡尔树。

例如，给定序列\(\{8,15,3,4,1,5,12,10,18,6 \}\)，则生成的最小堆笛卡尔树如图所示。

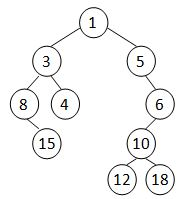
现在，给定一个长度为\(N\)的原始序列，请你生成最小堆笛卡尔树，并输出其层序遍历序列。

题目链接：https://www.acwing.com/problem/content/4282/

数据范围

\(1 \leq N \leq 30\)

思路

思路很简单，递归建树。每次找到区间最小值，将左边区间作为左子树，右边区间作为右子树，然后递归下去即可。

本题难点在于递归需要传什么参数。在这道题当中，传入参数为区间的左端点和右端点，返回根节点的下标。

代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 55;

int n;
int a[N], L[N], R[N];

int build(int l, int r)
{
    int mi = 2147483647, root;
    for(int i = l; i <= r; i ++) {
        if(a[i] < mi) {
            mi = a[i];
            root = i;
        }
    }
    if(root - 1 >= l) L[root] = build(l, root - 1);
    if(r >= root + 1) R[root] = build(root + 1, r);
    return root;
}

void bfs(int u)
{
    queue<int> que;
    que.push(u);
    while(que.size()) {
        int t = que.front();
        que.pop();
        printf("%d ", a[t]);
        if(L[t]) que.push(L[t]);
        if(R[t]) que.push(R[t]);
    }
}

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++) scanf("%d", &a[i]);
    int root = build(1, n);
    bfs(root);
    return 0;
}