第3章 图嵌入

简介

图嵌入（Graph Embedding）的目的是将给定图中的每个节点映射到一个低维的向量表示。这种向量表示通常被称为节点嵌入（Node Embedding），它保留了原图中节点的一些关键信息。图中的节点可以从两个域观察：一是原图域，其中节点通过边彼此连接；二是嵌入域，其中每个节点被表示为连续的向量。因此，从这两个域的角度来看，图嵌入的目标是将每个节点从图域映射到嵌入域，使得图域中的信息可以保留在嵌入域中。

这里有两个关键的问题，一个是哪些信息需要被保留？其答案是节点的邻域信息、节点的结构角色、社区信息和节点状态。另一个问题是，如何保留这些信息？解决这个问题的核心思想就是利用嵌入域中的节点表示重构要保留的图域信息。

下面给出图嵌入的通用框架：

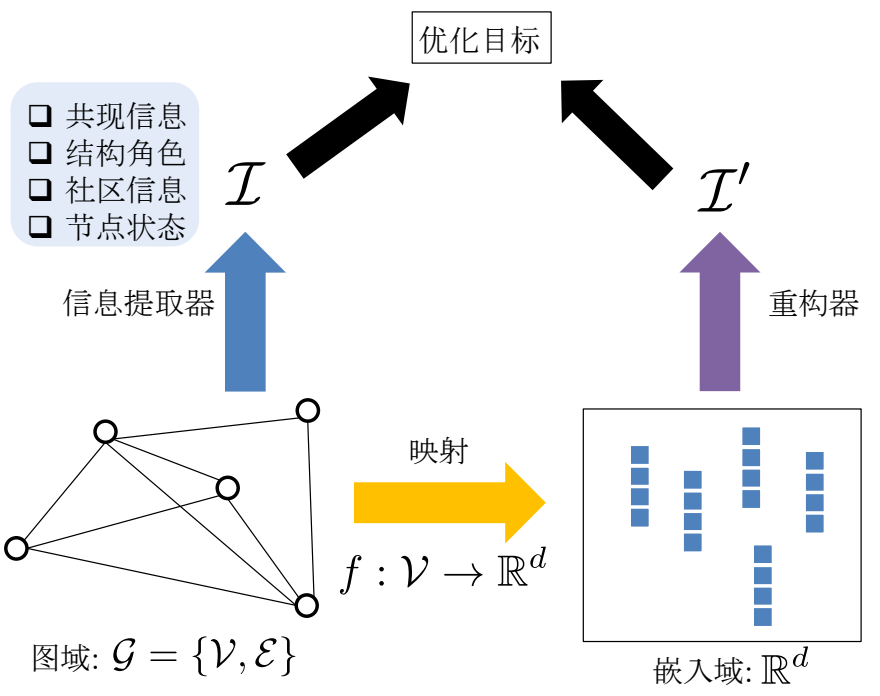
如图所示，图嵌入的通用框架有四个关键组件：

• 将节点从图域映射到嵌入域的映射函数
• 提取图域中需要保留的关键信息\(I\)的信息提取器
• 利用嵌入域的嵌入重新构造所提取的图信息\(I\)的重构器，重构的信息表示为\(I'\)
• 通过对基于提取的信息\(I\)和重构的信息\(I'\)的目标进行优化，学习映射和（或）重构器中涉及的所有参数

简单图的图嵌入

简单图是静态的、无向的、无符号的和同质的。可以按照保留的信息对算法进行分类，这些信息包括：节点共现、结构角色、节点状态和社区结构

保留节点共现

保留图中节点共现的流行方法之一是执行随机游走。如果一些节点倾向于在某些随机游走中共同出现，则认为这些节点是相似的。接着优化一个映射函数，使得学习到的节点表示能够重构出随机游走中提取的“相似性”。保留节点间共现关系的经典图嵌入算法是DeepWalk。

映射函数

映射函数\(f(v_i) = \boldsymbol{u}_i = \boldsymbol{W}^T \boldsymbol{e}_i\)。其中\(\boldsymbol{e}_i\)为one-hot向量，对于节点\(v_i\)，\(\boldsymbol{e}_i\)只有第\(i\)个元素是\(1\)，其余元素是\(0\)。矩阵\(\boldsymbol{W}\)的第\(i\)行是节点\(v_i\)的表示。

基于随机游走的共现提取器

给定一个图G中的起始节点\(v^{(0)}\)，从它的邻居中随机选中（一般是等概率）一个节点并前进到这个节点，接着从该选中的节点开始重复上述过程，直到一共访问了\(T\)个节点，这样就能得到一个节点的序列。这些被访问的节点组成的序列是图上长度为\(T\)的随机游走。

为了生成随机游走能够捕获整个图的信息，每个节点都被用作起始节点生成\(\gamma\)个随机游走。因此，在遍历整个图后，总共会获得\(|V|\cdot \gamma\)个随机游走。

将这些随机游走看作是自然语言中的句子，然后使用Skip-gram算法，保存节点间的共现关系。具体来说，两个节点的共现被表示为元组\((v_{con}, v_{cen})\)，其中\(v_{cen}\)表示中心节点，\(v_{con}\)表示它的某个上下文节点。对于每个随机游走，遍历其中的节点，将所有的共现关系添加到共现列表\(I\)中。

重构器和目标

为了通过嵌入域重构共现信息，需要通过节点嵌入推断在\(I\)中各个元组出现的概率。任意给定的元组\((v_{con}, v_{cen}) \in I\)中都有两种节点角色，即中心节点\(v_{cen}\)和上下文节点\(v_{con}\)。一个节点可以同时扮演两个角色，即中心节点和其他节点的上下文节点。因此，两个不同的映射函数被用于生成节点扮演两种不同角色时的表示：\(f_{cen}(v_i) = \boldsymbol{W_{cen}}^T \boldsymbol{e}_i\)和\(f_{con}(v_i) = \boldsymbol{W_{con}}^T \boldsymbol{e}_i\)。

对于一个元组\((v_{con}, v_{cen})\)，共现关系可以解释为在中心节点\(v_{cen}\)的上下文中观察\(v_{con}\)。通过\(f_{con}\)和\(f_{cen}\)两个映射函数与Softmax函数，对在\(v_{cen}\)的上下文中观察\(v_{con}\)的概率进行建模，如下所示：

\[p(v_{con}|v_{cen}) = \frac{exp(f_{con}(v_{con})^T)f_{cen}(v_{cen})}{\sum\limits_{v \in V}exp(f_{con}(v)^T)f_{cen}(v_{cen})} \]

假设共现列表\(I\)中的这些元组是相互独立的，因此重构\(I\)的概率可以建模如下：

\[I' = \prod_{(v_{con}, v_{cen}) \in I} p(v_{con}|v_{cen}) \]

由于\(I\)中存在重复的元组。为了去掉重复项，可以将其重新表述如下：

\[\prod_{(v_{con}, v_{cen}) \in set(I)} p(v_{con}|v_{cen})^{\#(v_{con}, v_{cen})} \]

为了使得更加准确地重构原图信息，因此要使得概率尽可能大，因此可以定义损失函数为上式的负对数。

加速学习过程

（1）分层Softmax
为了降低计算复杂度，可以先建立二叉树，然后通过根节点到节点\(v_con\)的路径对概率\(p(v_{con}|v_{cen})\)建模。给定由树节点序列\((p^{(0)}, p^{(1)})\)