第2章 图论基础
简介
本章将主要介绍以下内容:
- 图的表示
- 图的性质
- 复杂图
- 图上的计算任务
图的表示
- 图的定义:一个图可以被表示为\(G = \{V, E\}\),其中\(V = \{v_1, \dots, v_N\}\)是大小为\(N = |V|\)的节点集合,\(E = \{e_1, \dots, e_M\}\)是大小为\(M\)的边的集合。
注意:在没有特殊说明的情况下,本章只讨论无向图。
- 邻接矩阵:描述图的一个\(N \times N\)的01矩阵\(\boldsymbol{A}\)。如果点\(v_i\)和点\(v_j\)之间有边,则\(\boldsymbol{A_{i, j}} = 1\);反之,\(\boldsymbol{A_{i, j}} = 0\)
例子:
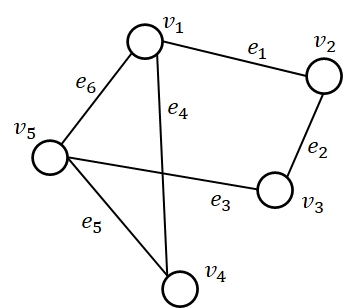

图的性质
度
- 度(Degree):度表示这个节点和其他节点相邻的次数,一般用\(d(v_i)\)来表示
- 邻域(Neighborhood):节点\(v_i\)的邻域\(N(v_i)\)是所有和它相邻的节点的集合。
- 定理(握手定理):一个图中所有节点的度之和是图中边的数量的两倍
- 推论:无向图邻接矩阵的非零元素的个数是边的数量的两倍
连通度
- 途径(Walk):图的途径是节点和边的交替序列,从一个节点开始,以一个节点结束,其中每条边与紧邻的节点相关联。途径的长度是途径中包含边的数量。
- 迹(Trail):迹是边各不相同的途径
- 路(Path):路是节点各不相同的途径,也称路径
- 定理:对于图\(G\)及其邻接矩阵\(\boldsymbol{A}\),用\(\boldsymbol{A}^n\)表示该邻接矩阵的\(n\)次幂。那么\(\boldsymbol{A}^n\)的第\(i\)行第\(j\)列的元素等于长度为\(n\)的\(v_i-v_j\)途径的个数(数学归纳法可证)
- 子图(Subgraph):图\(G\)的一个子图由\(G\)节点集的子集和边集的子集组成,并且子图的节点集必须包含边集涉及的所有节点。
- 连通分量(Connected Component):给定一个图\(G\),若一个子图任意一对节点之间都至少存在一条路,并且子图中的任何节点都不与除子图节点外的其他节点相连,那么这个子图就是一个连通分量。
- 连通图(Connected Graph):图中任意一对节点之间都至少存在一条路,即图中只有一个连通分量。
- 最短路(Shortest Path):给定连通图中的任意两点,连接这两点的长度最小的路被称为这两点之间的最短路。最短路的长度被称为两点间的距离。
- 图的直径(Diameter):图中最长的最短路的长度。
中心性
节点的中心性(Centrality)用来衡量节点在图上的重要程度。
- 度中心性(Degree Centrality):利用节点的度来衡量节点的重要性(有多少人认为你厉害),即:\(c_d(v_i) = d(v_i) = \sum\limits_{j = 1}^N \boldsymbol{A_{i, j}}\)
- 特征向量中心性(Eigenvector Centrality):衡量节点的中心性时同时考虑邻居节点的中心性(认为你厉害的人有多厉害),即:\(c_e(v_i) = \frac{1}{\lambda}\sum\limits_{j = 1}^N \boldsymbol{A_{i, j}} \cdot c_e(v_j) \Rightarrow \lambda \cdot \boldsymbol{c_e} = \boldsymbol{A} \cdot \boldsymbol{c_e}\)。显然,\(\boldsymbol{c_e}\)是矩阵的特征向量,\(\lambda\)是对应的特征值。中心性的值通常为正数,所以选择中心性需要考虑所有元素均为正数的特征向量。根据Perron-Frobenius定理,一个元素全为正的实方阵具有唯一的最大特征值,其对应的特征向量的元素全为正。因此可以选择最大的特征值\(\lambda\),将它的相应的特征向量作为中心性向量。
- Katz中心性(Katz Centrality):是特征向量中心性的一个变体,不仅考虑邻居的中心性,还考虑了自己的中心性(你认为自己厉害),即:\(c_k(v_i) = \alpha \sum\limits_{j=1}^N \boldsymbol{A_{i,j}}c_k(v_j) + \beta\)。将其用矩阵表示,\(c_k = \alpha \boldsymbol{A}c_k + \beta \Rightarrow (\boldsymbol{I} - \alpha \boldsymbol{A})c_k = \beta\)。\(\alpha\)太大会导致方程无意义,太小会使得中心性没有意义。在实践中,经常令\(\alpha < \frac{1}{\lambda_{\max}}\),这就保证了矩阵\(\boldsymbol{I} - \alpha \boldsymbol{A}\)的可逆性。那么\(c_k\)可以按照如下方式计算:\(c_k = (\boldsymbol{I} - \alpha \boldsymbol{A})^{-1} \beta\)。
- 介数中心性(Betweenness Centrality):检查节点是否在图中处于重要位置。节点\(v_i\)的介数中心性可以定义为:\(c_b(v_i) = \sum\limits_{v_s \neq v_i \neq v_t} \frac{\sigma_{st}(v_i)}{\sigma_{st}}\)。其中\(\sigma_{st}\)表示所有从节点\(v_s\)到节点\(v_t\)的最短路数目,\(\sigma_{st}(v_i)\)表示这些路中经过节点\(v_i\)的路的数目。显然,介数中心性的值会随着图的增大而增大,因此需要进行归一化处理。一种有效的方法是将所有节点的中心性除以其中的最大值。当任意一对节点之间的最短路都通过节点\(v_i\)时,介数中心性达到最大值,即\(\frac{\sigma_{st}(v_i)}{\sigma_{st}} = 1\)。在一个无向图中,共有\(\frac{(N - 1)(N - 2)}{2}\)个不包含节点\(v_i\)的节点对,所以介数中心性的最大值是\(\frac{(N - 1)(N - 2)}{2}\)。所以\(v_i\)归一化后的介数中心性\(c_{nb}(v_i)\)可以定义为:\(c_{nb}(v_i) = \frac{2 \times \sum\limits_{v_s \neq v_i \neq v_t} \frac{\sigma_{st}(v_i)}{\sigma_{st}}}{(N - 1)(N - 2)}\)
复杂图
- 异质图(Heterogeneous Graphs):节点的种类可以有多种,边的种类也可以有多种。如:描述出版物及其引用关系的学术网络中,有三种类型的节点(作者、论文、会议),不同类型的边描述不同类型节点之间的不同关系。
- 二分图(Bipartite Graphs):节点集被分为两个不相交的子集,每一子集内的任意点之间没有边相连接。如:用户与商品之间的购买关系。
- 多维图(Multi-dimensional Graphs):同一对节点之间存在多种不同的关系。如:淘宝网,用户与商品之间存在着多种不同的行为(点击、购买、评论)。
- 符号图(Signed Graphs):边集可以被分为两个不相交的子集,这两个子集分别包含正边和负边。如:社交网络中,用户可以关注和屏蔽其他用户。
- 超图(hypergraphs):超边可以描述超越两两之间关系的更高维度的关系,如:
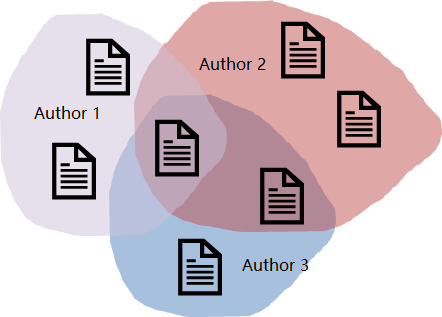
- 动态图(Dynamic Graphs):图中的每个节点或每条边都与时间戳相关联,如:

图的计算任务
图上有各种各样的计算任务,这些任务主要分为两大类:
- 节点任务,整个数据通常表示为一个图,节点作为数据样本
- 图任务,数据往往包括一组图,每个数据样本是一个图
侧重于节点的任务
- 节点分类
- 链接预测
侧重于图的任务
- 图分类


 浙公网安备 33010602011771号
浙公网安备 33010602011771号