笔记4：多层感知器（自定义模型）

导入相关库

import torch
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from torch import nn
import torch.nn.functional as F
%matplotlib inline

数据预处理

查看数据相关信息

data = pd.read_csv('E:/datasets2/1-18/dataset/daatset/HR.csv')

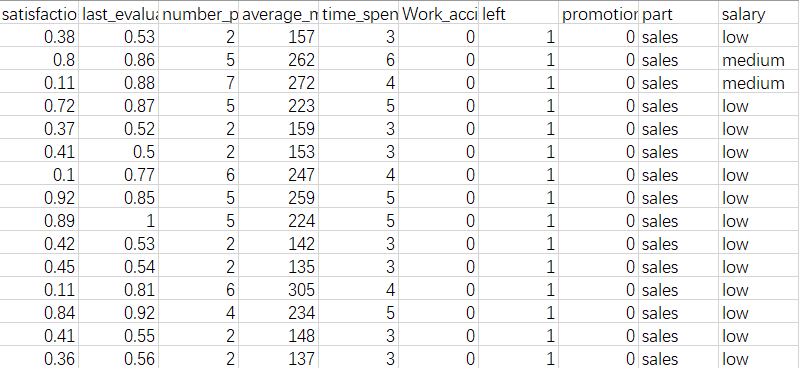
先通过data.info()查看数据的相关信息

由于part和salary都是object类型，因此需要查看都是什么值
分别调用data.part.unique()和data.salary.unique()，结果如下：

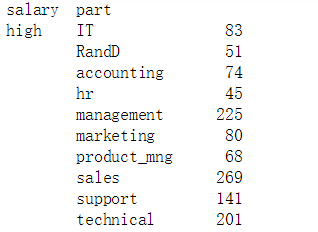
（让我们看一下职业与收入的关系吧，调用data.groupby(['salary', 'part']).size()，结果如下：

数据预处理

我们可以将part和salary用one-hot编码来表示，并且把原来的part和salary删除

data = data.join(pd.get_dummies(data.salary))
del data['salary']
data = data.join(pd.get_dummies(data.part))
del data['part']

定义数据

Y_data = data.left.values.reshape(-1, 1)
Y = torch.from_numpy(Y_data).type(torch.FloatTensor)
X_data = data[[col for col in data.columns if col != 'left']].values
X = torch.from_numpy(X_data).type(torch.FloatTensor)

这里是学习其他特征与left的关系，left取值有两个，分别是0和1。

自定义模型

class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear_1 = nn.Linear(20, 64)
        self.linear_2 = nn.Linear(64, 64)
        self.linear_3 = nn.Linear(64, 1)
        self.relu = nn.ReLU()
        self.sigmoid = nn.Sigmoid()
    def forward(self, input):
        x = self.linear_1(input)
        x = self.relu(x)
        x = self.linear_2(x)
        x = self.relu(x)
        x = self.linear_3(x)
        x = self.sigmoid(x)
        return x

几个注意点：

• super().__init__() 继承父类
• linear_1的输入是20，因为有20个特征，输出是64，因为设置的隐藏层数为64；linear_3的输出是1，因为最后是输出一个值

因为nn.ReLU()和nn.Sigmoid()没有参数，因此可以采用更加简单并且常用的写法：

class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear_1 = nn.Linear(20, 64)
        self.linear_2 = nn.Linear(64, 64)
        self.linear_3 = nn.Linear(64, 1)
    def forward(self, input):
        x = F.relu(self.linear_1(input))
        x = F.relu(self.linear_2(x))
        x = F.sigmoid(self.linear_3(x))
        return x

然后用如下代码获得一个模型：

def get_model():
    model = Model()
    optimizer = torch.optim.Adam(model.parameters(), lr = 0.0001)
    return model, optimizer

model, optimizer = get_model()
loss_func = nn.BCELoss()

参数定义

batch_size = 64
num_batch = len(data) // batch_size
epochs = 100

训练过程

for epoch in range(epochs):
    for i in range(num_batch):
        start = i * batch_size
        end = start + batch_size
        x = X[start: end]
        y = Y[start: end]
        y_pred = model(x)
        loss = loss_func(y_pred, y)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
    with torch.no_grad():
        print('epoch: ', epoch, 'loss: ', loss_func(model(X), Y).data.item())

几个关键点：

• .item()方法可以获得数值
• 因为输出损失函数的值，这部分的计算不能积累梯度，因此要在torch.no_grad()下进行