软工结队博客
[软工]结对项目作业
| 项目 | 内容 |
|---|---|
| 这个作业属于哪个课程 | 2020春季计算机学院软件工程(罗杰 任健) |
| 这个作业的要求在哪里 | 结对项目作业 |
| 我在这个课程的目标是 | 学习工程化开发软件,体验团队开发和结队开发 |
| 这个作业在哪个具体方面帮助我实现目标 | 体验结队编程的过程 |
| 班级 | 006 |
| 项目地址 | https://github.com/BUAA-SE/extremely-weak-GeoGebra |
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | 估计这个任务需要多少时间 | 10 | 10 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 100 | 180 |
| · Design Spec | 生成设计文档 | 50 | 70 |
| · Design Review | 设计复审 (和同事审核设计文档) | 40 | 50 |
| · Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 50 | 80 |
| · Design | 具体设计 | 80 | 100 |
| · Coding | 具体编码 | 300 | 500 |
| · Code Review | 代码复审 | 50 | 70 |
| · Test | 测试(自我测试,修改代码,提交修改) | 150 | 240 |
| Reporting | 报告 | ||
| ·Test Report | 测试报告 | 30 | 40 |
| ·Size Measurement | 计算工作量 | 20 | 20 |
| ·Postmortem & Process Improvement Plan | 事后总结, 并提出过程改进计划 | 20 | 30 |
| ·Size Measurement | 合计 | 900 | 1290 |
3.看教科书和其它资料中关于 Information Hiding,Interface Design,Loose Coupling 的章节,说明你们在结对编程中是如何利用这些方法对接口进行设计的。
- 关于信息隐藏的原则,我们设计的类有许多私有的方法和属性,仅开放了极其有限的部分作为public,例如我们的核心的core类,仅提供了ui界面可能会用到的部分方法,例如
addLine和delLine方法, - 关于接口设计,我们提供了一个core类,core类中包括了ui需要用到的各种方法,这样,我们之后的改动都可以仅仅在core类中进行修改即可,使得各部分之间的耦合性就大大降低了,同时我们还设计了get和set方法,进一步确保了接口的安全性
- 关于松耦合,例如line和circle类之间是几乎完全不产生依赖的,同时,我们将整体的代码用core类来统一,其他各个类之间几乎是不产生依赖的,例如
computationalGeometry类和skipList类等
4.计算模块接口的设计与实现过程。设计包括代码如何组织,比如会有几个类,几个函数,他们之间关系如何,关键函数是否需要画出流程图?说明你的算法的关键(不必列出源代码),以及独到之处
最主要的有三个类,一个是计算几何相关的computationalGeometry类,一个是扫描线算法要用到的数据结构skipList类,一个是计算模块Core类。
其中Core类和skipList类都会用到computationalGeometry类,当然Core类还会用到skipList类。
然后就是和基本上次一样的点类,直线类,圆类,就不再具体叙述。
在具体实现时,我对于不同规模的数据采取了不同的算法,当数据范围较小时采用bruteForce()暴力算法,当数据规模教大的时候采用sweepLine()扫描线算法。
$bruteForce$()
做法基本和上次相同,唯一不同的是加入了判断点是否在当前的几何对象上的判断,并对直线结构体进行了修改,代码如下:
struct Line {
int id;//直线编号
char tp;//'L', 'S', 'R'
Point u;
Vector v;
//假设输入为点A和点B,则u = A, v是向量AB
}
bool computationalGeometry::pointOnSegment(const Point& A, const Line& L) {
//A一定是在L所在的直线上,利用点积判断A具体的位置
if (L.tp == 'L') return true;
if (L.tp == 'R') {
return dcmp((A - L.u) * L.v) >= 0;
}
return dcmp((A - L.u) * (A - (L.u + L.v))) <= 0;
}
$sweepLine()$
传统的扫描线做法是用来处理$n$条线段的交点问题,在这里我们需要支持直线和射线,这也是我做法关键之处:把直线和射线都转化成线段然后直接跑扫描线。根据题目所给的范围可以求出,任意两个几何对象的交点坐标范围是在$1e10$这个级别,大概3e10, 4e10的样子,于是我把所有直线和射线都在$x=1e11$和$x=-1e11$处截取,这样就全部变成了线段。
至于独到之处,大概是处理了网上算法处理不了的多线共点的情况。我每次会和某一个时间点相关的全部几何对象拿出来一起处理。当两条线段的交在当前事件点时,为了保证他们是良序的,根据情况把$1e11$和$-1e11$带入计算,即使用他们在交换之后的大小关系或者交换之前的大小关系。
在具体处理时,我是按照先插入,如果产生的交点和当前时间点相同,则把相关线段继续提取出来。网上的做法是交换相交的两条线段的位置,多条线段的时候则需要把他们直接翻转。于是我先从跳表中删除了需要翻转但是不需要删除的线段,再删除了需要删除的线段,同时判断它相邻的两个线段是否产生了新的交点。接下来再把需要翻转的线段重新插入了回去,之所以能做到翻转是因为我会根据情况来判断他们的大小关系,同时判断它和它相邻的两条线段是否有交点。
同时,因为巨大的精度误差,假设直线$l$和直线$m$交于点$A$,把$A$的横坐标带入直线以后算出来的纵坐标的误差很大,于是我改成了再一次求直线$l$和直线$m$的交点,判断他们的交点的横坐标和当前事件点的横坐标是否相同。但是这样仍然有精度问题,lineIntersectionWithLine(L1, L2)和lineIntersectionWithLine(L2, L1)求出来的交点不同,于是我求交点的时候保证$L1.id<L2.id$,这样就没有问题。说起来简单,debug的时候改了一年,C++有bigDecimal多好。
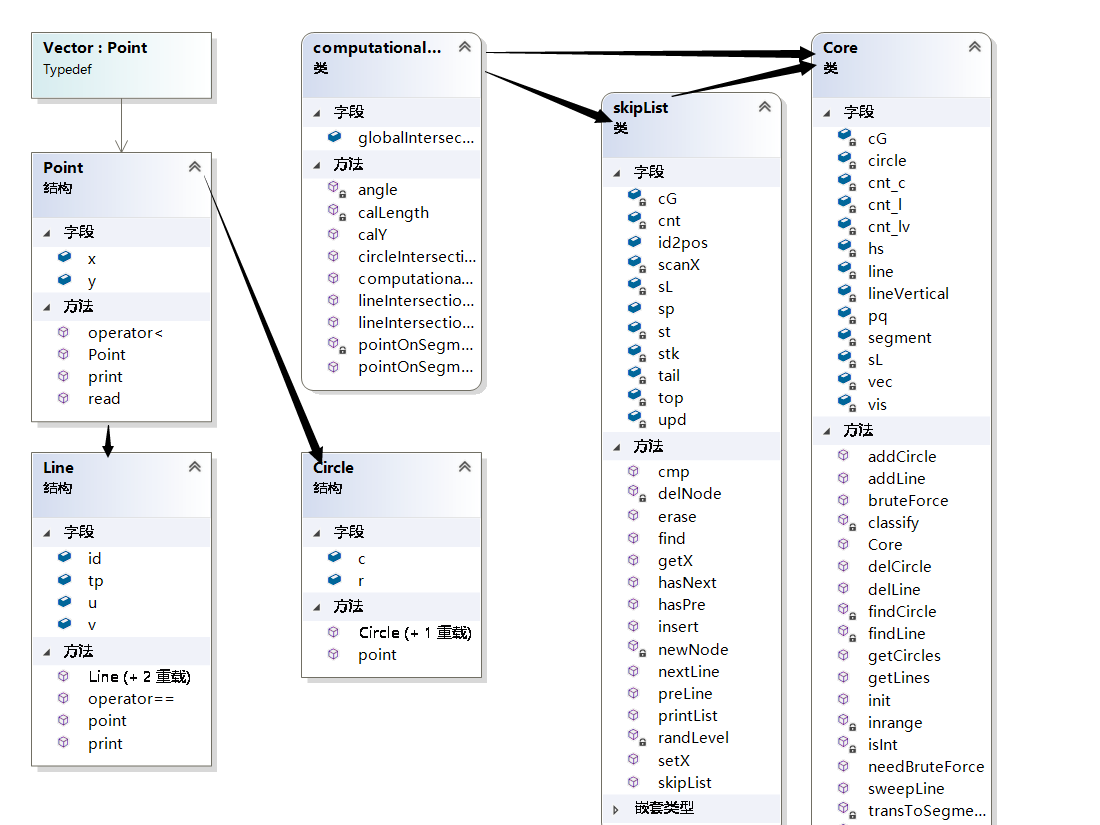
5.阅读有关 UML 的内容。画出 UML 图显示计算模块部分各个实体之间的关系(画一个图即可)。
这里说明一下,由于计算模块的代码主要是由一名队员完成的,所以我们的这一部分的类图基本上是一致的.
6.算模块接口部分的性能改进。记录在改进计算模块性能上所花费的时间,描述你改进的思路,并展示一张性能分析图(由VS 2015/2017的性能分析工具自动生成),并展示你程序中消耗最大的函数。
暴力部分的性能还是不错的,没有花时间在这部分进行优化,主要还是对扫描线算法部分进行的性能改进。
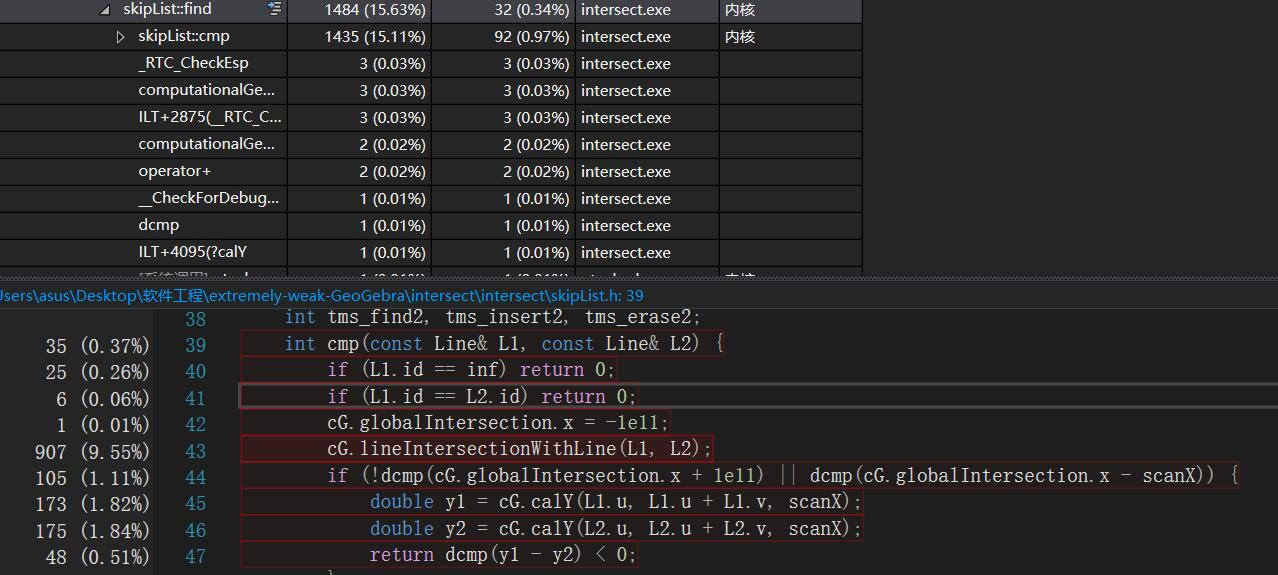
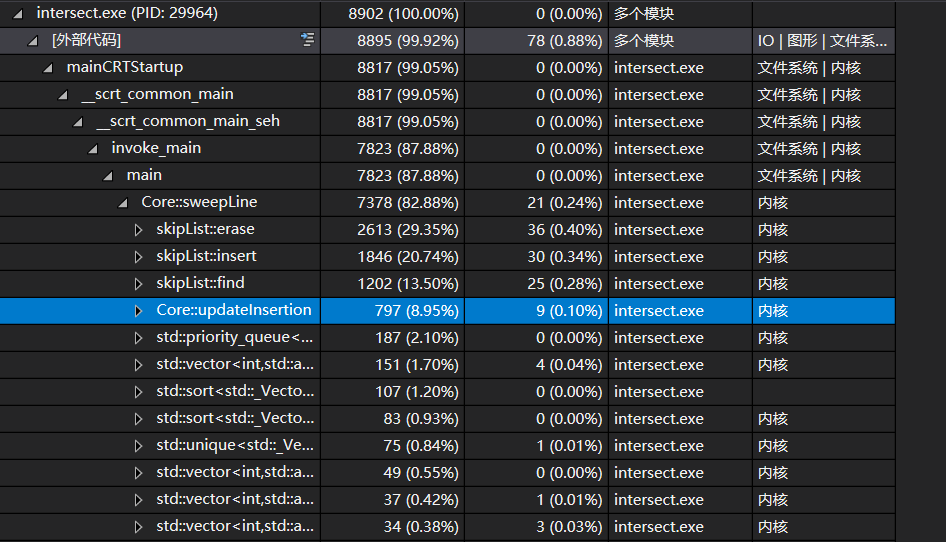
可以看出,跳表的删除、查找、插入操作花了大量的时间,其中很大一部分花在了算交点上。我发现在算交点的时候有冗余的判断,在大量的调用下会浪费很多时间,去掉以后快了不少。
然后我发现查找其实可以在插入的时候把线段的编号和跳表的节点绑定起来,这样就可以做到$O(1)$查找,直接就优化掉了$\frac{1}{3}$的时间下来。
最后性能的瓶颈就只剩下$insert$和$erase$,对于我每次要删除和插入的线段,他们在跳表中的位置是相邻的,利用这个性质可以省去很多不必要的比较,但是我还有很多其他课程要学习,所以没有再继续优化。
这些函数单次的时间其实很少,主要是调用次数特别的庞大,在这里展示一下比较部分的代码,总的来说它耗时最多。
int cmp(const Line& L1, const Line& L2) {
if (L1.id == inf) return 0;
if (L1.id == L2.id) return 0;
if (dcmp(L1.v ^ L2.v)) {
if (L1.id < L2.id) {
Vector u = L1.u - L2.u;
double t = (L2.v ^ u) / (L1.v ^ L2.v);
cG.globalIntersection = L1.u + L1.v * t;
}
else {
Vector u = L2.u - L1.u;
double t = (L1.v ^ u) / (L2.v ^ L1.v);
cG.globalIntersection = L2.u + L2.v * t;
}
}
else {
return dcmp(cG.calY(L1.u, L1.u + L1.v, scanX) - cG.calY(L2.u, L2.u + L2.v, scanX)) < 0;
}
if (dcmp(cG.globalIntersection.x - scanX)) {
return dcmp(cG.calY(L1.u, L1.u + L1.v, scanX) - cG.calY(L2.u, L2.u + L2.v, scanX)) < 0;
}
if (sp < 0) {
return dcmp(cG.calY(L1.u, L1.u + L1.v, -1e11) - cG.calY(L2.u, L2.u + L2.v, -1e11)) < 0;
}
return dcmp(cG.calY(L1.u, L1.u + L1.v, 1e11) - cG.calY(L2.u, L2.u + L2.v, 1e11)) < 0;
}
7.看 Design by Contract,Code Contract 的内容:描述这些做法的优缺点,说明你是如何把它们融入结对作业中的。
优点:
- 给程序员提供了一种规范,使得其能够非常具体的规定一个模块,包括这个模块的调用前后的过程,
- 很大程度上确保了程序的正确性和规范性,减少了代码出现bug的风险,也大大方便了测试.
- 为编程提供一定的指导价值
缺点:
-
影响编程,程序员更多的去考虑这些规范而不是模块功能本身
-
编程的限制过多,编程效率下降.
在结队作业中,我们对core类进行了一些契约,比如要求其中必须含有存储交点的容器,和存储线和圆的容器,同时要求core类中必须有add方法和del方法,如果使用add方法则必须保证add之后,在存储线容器中必须增加add之后的线,并且一旦计算完交点,则必须对存储交点的容器进行一次更新操作.
8.计算模块部分单元测试展示。展示出项目部分单元测试代码,并说明测试的函数,构造测试数据的思路。并将单元测试得到的测试覆盖率截图,发表在博客中。要求总体覆盖率到 90% 以上,否则单元测试部分视作无效。
我们的core部分的代码是以一个core类串联起整个代码的,在core类中主要有5大方法分别是addLine,delLine,addCircle,delCircle,bruteForce,所以我们的单元测试也主要围绕着四部分展开,对于添加和删除的方法,其代码比较简单,我们主要对其进行了异常的测试,对于bruteForce方法,是我们的核心方法,它用来计算core类中的交点,所以我们的单元测试也围绕着这一方法展开.我们将其分为三大部分进行测试,分别是线与线的测试,线与圆的测试,圆与圆的测试
线与线的测试
在线与线的测试中,我们又分为直线有交点,直线无交点,线段有交点,线段无交点,射线有交点,射线无交点,以及直线与射线与线段的混杂测试七个小类
测试代码如下:
core.init();
//直线有交点
core.addLine(Point(0, 0), Point(3, 6), 'L');
core.addLine(Point(0, 1), Point(1, 2), 'L');
Assert::AreEqual(core.bruteForce(), (int)1);
//直线无交点
core.init();
core.addLine(Point(0, 0), Point(1, 2), 'L');
core.addLine(Point(1, 3), Point(3, 7), 'L');
Assert::AreEqual(core.bruteForce(), (int)0);
//射线有交点
core.init();
core.addLine(Point(0, 0), Point(3, 6), 'R');
core.addLine(Point(2, 0), Point(2, 5), 'R');
Assert::AreEqual(core.bruteForce(), (int)1);
//射线无交点
core.init();
core.addLine(Point(0, 0), Point(1, 2), 'R');
core.addLine(Point(-7, -7), Point(-9, -9), 'R');
Assert::AreEqual(core.bruteForce(), (int)0);
//线段有交点
core.init();
core.addLine(Point(0, 0), Point(3, 6), 'S');
core.addLine(Point(2, 0), Point(2, 5), 'S');
Assert::AreEqual(core.bruteForce(), (int)1);
//线段无交点
core.init();
core.addLine(Point(0, 0), Point(1, 2), 'S');
core.addLine(Point(-7, -7), Point(-9, -9), 'S');
Assert::AreEqual(core.bruteForce(), (int)0);
//直线,射线,线段混合
core.init();
core.addLine(Point(0, 0), Point(2, 2), 'L');
core.addLine(Point(0, 2), Point(2, 0), 'S');
core.addLine(Point(1, 2), Point(-1, 3), 'S');
core.addLine(Point(-1, 0), Point(2, 3), 'R');
core.addLine(Point(-1, 0), Point(-2, 4), 'R');
core.addLine(Point(-2, 0), Point(0, -1), 'R');
Assert::AreEqual(core.bruteForce(), (int)5);
线与圆的测试
在线与圆的测试中,我么分为了直线与圆有交点,直线与圆无交点,线段与圆有交点,线段与圆无交点,射线与圆有交点,射线与圆无交点,以及直线与射线与线段与圆的混杂七大类
core.init();
core.addLine(Point(1, 2), Point(3, 6), 'L');
core.addCircle(Point(0, 0), 10);
Assert::AreEqual(core.bruteForce(), (int)2);
core.init();
core.addLine(Point(1, 2), Point(3, 6), 'L');
core.addCircle(Point(5, -5), 1);
Assert::AreEqual(core.bruteForce(), (int)0);
core.init();
core.addLine(Point(0, 2), Point(0, 5), 'R');
core.addCircle(Point(0, 0), 2);
Assert::AreEqual(core.bruteForce(), (int)1);
core.init();
core.addLine(Point(0, 3), Point(0, 5), 'R');
core.addCircle(Point(0, 0), 1);
Assert::AreEqual(core.bruteForce(), (int)0);
core.init();
core.addLine(Point(-1, 0), Point(1, 0), 'S');
core.addCircle(Point(0, 0), 1);
Assert::AreEqual(core.bruteForce(), (int)2);
core.init();
core.addLine(Point(0, 0), Point(0, 1), 'S');
core.addCircle(Point(0, 0), 10);
Assert::AreEqual(core.bruteForce(), (int)0);
core.init();
core.addLine(Point(0, 0), Point(20, 20), 'L');
core.addLine(Point(0, 20), Point(20, 0), 'S');
core.addLine(Point(10, 20), Point(-10, 30), 'S');
core.addLine(Point(-10, 0), Point(20, 30), 'R');
core.addLine(Point(-10, 0), Point(-20, 40), 'R');
core.addLine(Point(-20, 0), Point(0, -10), 'R');
core.addCircle(Point(0, 0), 40);
core.addCircle(Point(30, 0), 10);
core.addCircle(Point(0, 0), 20);
core.addCircle(Point(100, 100), 30);
Assert::AreEqual(core.bruteForce(), (int)23);
圆与圆的测试
在圆与圆的测试中我们测试了外离,外切,内含,内切,相交五大类
core.init();
core.addCircle(Point(0, 0), 10);
core.addCircle(Point(0, 0), 1);
Assert::AreEqual(core.bruteForce(), (int)0);
core.init();
core.addCircle(Point(0, 0), 1);
core.addCircle(Point(5, 0), 1);
Assert::AreEqual(core.bruteForce(), (int)0);
core.init();
core.addCircle(Point(0, 0), 10);
core.addCircle(Point(1, 0), 10);
Assert::AreEqual(core.bruteForce(), (int)2);
core.init();
core.addCircle(Point(0, 0), 1);
core.addCircle(Point(2, 0), 1);
Assert::AreEqual(core.bruteForce(), (int)1);
core.init();
core.addCircle(Point(0, 0), 3);
core.addCircle(Point(2, 0), 1);
Assert::AreEqual(core.bruteForce(), (int)1);
异常测试
异常测试的测试内容见下一项问题,异常测试的代码如下.
core.init();
Assert::AreEqual(core.addLine(Point(0, 0), Point(3, 6), 'A'), -1);
Assert::AreEqual(core.addLine(Point(0, 0), Point(0, 0), 'L'), -2);
Assert::AreEqual(core.addLine(Point(1e6, 0), Point(0, 0), 'L'), -3);
Assert::AreEqual(core.addLine(Point(0, -1e6), Point(0, 0), 'L'), -3);
Assert::AreEqual(core.addLine(Point(0, 0), Point(1e6, 0), 'L'), -3);
Assert::AreEqual(core.addLine(Point(0, 0), Point(0, -1e6), 'L'), -3);
Assert::AreEqual(core.addLine(Point(0, 0), Point(3.3, 0), 'L'), -4);
Assert::AreEqual(core.addLine(Point(1.1, 0), Point(0, 0), 'L'), -4);
Assert::AreEqual(core.addLine(Point(0, 2.2), Point(0, 0), 'L'), -4);
Assert::AreEqual(core.addLine(Point(0, 0), Point(0, 4.4), 'L'), -4);
Assert::AreEqual(core.addLine(Point(0, 0), Point(1, 1), 'L'), 0);
Assert::AreEqual(core.addLine(Point(0, 0), Point(-1, -1), 'L'), -5);
core.init();
Assert::AreEqual(core.addLine(Point(0, 0), Point(1, 1), 'S'), 0);
Assert::AreEqual(core.addLine(Point(0, 0), Point(-1, -1), 'S'), 0);
Assert::AreEqual(core.addLine(Point(1, 1), Point(-1, -1), 'R'), -5);
core.init();
Assert::AreEqual(core.addLine(Point(0, 0), Point(2, 2), 'R'), 0);
Assert::AreEqual(core.addLine(Point(0, 1), Point(3, 4), 'R'), 0);
Assert::AreEqual(core.addLine(Point(-1, -1), Point(1, 1), 'R'), -5);
Assert::AreEqual(core.addLine(Point(0, 0), Point(-1, -1), 'R'), 0);
Assert::AreEqual(core.addLine(Point(0, 0), Point(10, 10), 'L'), -5);
core.init();
core.addCircle(Point(0, 0), -1);
core.addCircle(Point(999999, 999999), 1);
core.addCircle(Point(1.1, 0), 1);
core.addCircle(Point(0, 1.1), 1);
core.addCircle(Point(0, 0), 5);
core.addCircle(Point(0, 0), 5);
单元测试覆盖率
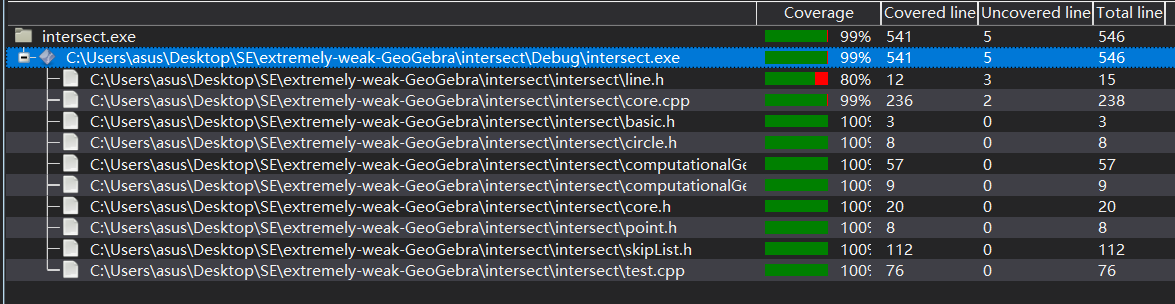
9.算模块部分异常处理说明。在博客中详细介绍每种异常的设计目标。每种异常都要选择一个单元测试样例发布在博客中,并指明错误对应的场景。
| 异常种类 | 错误场景 | 异常理由 | 单元测试样例 |
|---|---|---|---|
| 圆的半径为负数 | C 0 0 -1 | 圆的半径不可能为负数 | core.addCircle(Point(0, 0), -1); |
| 坐标超出范围 | C 0 0 9999999 | 不符合题目要求 | core.addCircle(Point(999999, 999999), 1); |
| 坐标是小数 | C 0 0 1.1 | 不符合1题目要求 | core.addCircle(Point(1.1, 0), 1); |
| 两个圆重合 | C 0 0 1 C 0 0 1 | 两个圆重合,交点有无数个 | core.addCircle(Point(0, 0), 5);core.addCircle(Point(0, 0), 5); |
| 输入的格式不符合规范 | A 0 0 Q 0 0 1 1 |
不符合要求的输入 | Assert::AreEqual(core.addLine(Point(0, 0), Point(3, 6), 'A'), -1); |
| 线的两个坐标相同 | L 0 0 0 0 | 无法从中推出线的表达式 | Assert::AreEqual(core.addLine(Point(0, 0), Point(0, 0), 'L'), -2); |
| 线重合 | L 0 0 1 1 R 0 0 1 1 |
线重合会产生无数个交点 | Assert::AreEqual(core.addLine(Point(0, 0), Point(1, 1), 'R'), 0); Assert::AreEqual(core.addLine(Point(0, 0), Point(1, 1), 'L'), 0); |
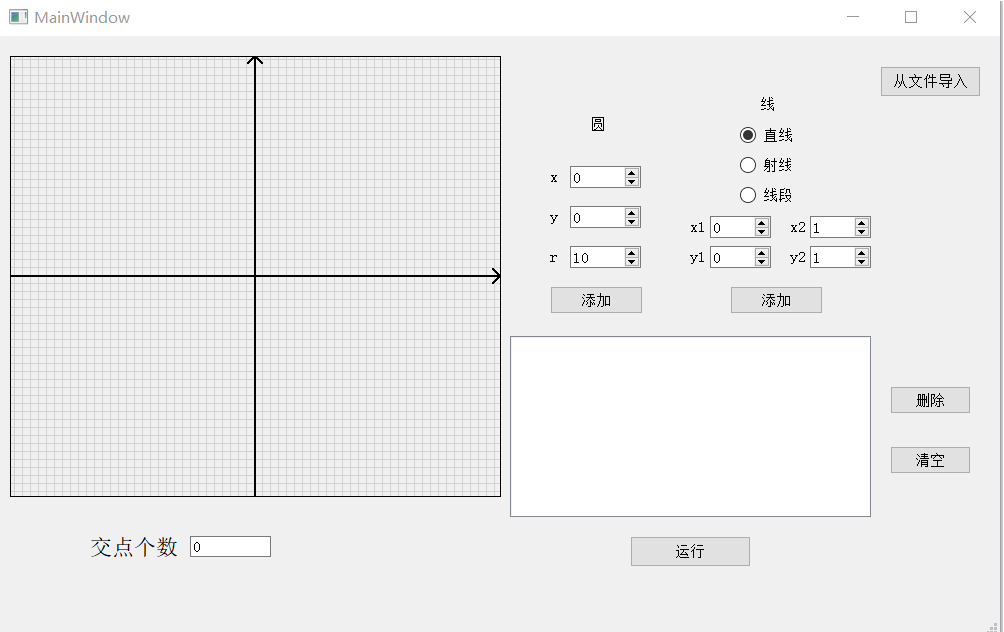
10.界面模块的详细设计过程。在博客中详细介绍界面模块是如何设计的,并写一些必要的代码说明解释实现过程。
-
使用qt进行ui设计
在查阅了一些资料以及进行了一些调研之后,我们决定使用qt进行ui模块的开发,使用的语言为c++,
-
坐标变换
在qt中坐标是以左上角为原点,向右为x轴,向下为y轴,我们需要将原点定位到坐标轴的中心,所以需要对每个坐标的x加上width/2,对于每个坐标的y,将其变换方向为向上,并加上height/2,
-
画布设计
首先对画布进行填充,使其被若干横线和总线进行方格化分割,然后画出x轴和y轴
//画边框 QPainter painter(ui->widget); QBrush brush("#D3D3D3"); QPen pen(QColor(0, 0, 0)); //pen.setWidth(3); brush.setStyle(Qt::CrossPattern); painter.setBrush(brush); painter.setPen(pen); painter.drawRect(0,0,width,height); //画坐标轴 QPen pen2(QColor(0, 0, 0)); pen2.setWidth(2); painter.setPen(pen2); painter.drawLine(0,height/2,width,height/2); painter.drawLine(width,height/2,width-7,height/2-7); painter.drawLine(width,height/2,width-7,height/2+7); painter.drawLine(width/2,0,width/2,height); painter.drawLine(width/2,0,width/2-7,7); painter.drawLine(width/2,0,width/2+7,7); -
添加和删除
添加:
可以选择圆和直线的类型,并输入相关的坐标和半径信息之后,点击添加按钮,即可自动生成一个"L x1 y2 x2 y2"或者"C x y r"的格式的信息并将其放入到文本框内
//添加圆 connect(ui->addButton1,&QPushButton::clicked,[=](){ if(ui->cir_r->value()>0){ line_qt cir; cir.type = 'C'; cir.x1 = ui->cir_x->value(); cir.y1 = ui->cir_y->value(); cir.x2 = ui->cir_r->value(); string name = "C "+to_string(cir.x1)+" "+to_string(cir.y1)+" "+to_string(cir.x2); QString name2= QString::fromStdString(name); QListWidgetItem * item = new QListWidgetItem(name2); ui->listWidget->addItem(item); } }); //添加直线 connect(ui->addButton2,&QPushButton::clicked,[=](){ char type; if(ui->isLine_L->isChecked()) type = 'L'; else if(ui->is_Line_R->isChecked()) type = 'R'; else if(ui->isLine_S->isChecked()) type = 'S'; else return; line_qt l; l.type = type; l.x1 = ui->line_x1->value(); l.y1 = ui->line_y1->value(); l.x2 = ui->line_x2->value(); l.y2 = ui->line_y2->value(); string name = ""; name.append(1,l.type); name = name+" "+to_string(l.x1)+" "+to_string(l.y1)+" "+to_string(l.x2)+" "+to_string(l.y2); QString name2= QString::fromStdString(name); QListWidgetItem * item = new QListWidgetItem(name2); ui->listWidget->addItem(item); });删除:
删除操作是先点击文本框内某一项,然后点击删除即可将其从文本框中删除.
//删除 connect(ui->del_button,&QPushButton::clicked,[=](){ int row = ui->listWidget->currentRow();//获取当前鼠标所选行 ui->listWidget->takeItem(row);//删除该行 }); //清空 connect(ui->clear_button,&QPushButton::clicked,[=](){ ui->listWidget->clear(); }); -
运行
点击运行,即可绘制出文本框中的线和圆,并计算交点的个数交点的个数在左下角呈现.
//运行 connect(ui->run_button,&QPushButton::clicked,[=](){ int size =ui->listWidget->count(); string str; stringstream ss; out.open(path,ios::out); char type; double x1,y1,x2,y2 = 0; // core.init(); out<<size<<"\n"; lines.clear(); for(int i=0;i<size;i++) { line_qt l; ss.clear(); str = ui->listWidget->item(i)->text().toStdString(); out<<str<<"\n"; ss<<str; ss>>type; if(type=='C'){ ss>>x1>>y1>>x2; } else{ ss>>x1>>y1>>x2>>y2; } l.type = type; l.x1 = x1; l.x2 = x2; l.y1 = y1; l.y2 = y2; lines.push_back(l); //addL(l); } out.close(); int inter_num; computationalGeometry cg; inter_num = cg.caclInter("input.txt"); QString st = QString::fromStdString(to_string(inter_num)); ui->lineEdit->setText(st); qDebug()<<inter_num<<endl; qDebug()<<st<<endl; // cg.test(); update(); }); -
导入
从文件进行线和圆的信息的导入,并将导入后的信息输入到文本框内,
//文件 connect(ui->fileButton,&QPushButton::clicked,[=](){ QString path = QFileDialog::getOpenFileName(this,"打开文件","C:\\Users"); QFile file(path); file.open(QIODevice::ReadOnly); ui->listWidget->clear(); QTextStream in(&file); int n; in>>n; char type; double x1,x2,y1,y2 = 0; for(int i = 0;i<n;i++){ in>>type; if(type=='C'){ in>>x1>>y1>>x2; string name = "C "+to_string(x1)+" "+to_string(y1)+" "+to_string(x2); QString name2= QString::fromStdString(name); QListWidgetItem * item = new QListWidgetItem(name2); ui->listWidget->addItem(item); } else{ in>>x1>>y1>>x2>>y2; string name = ""; name.append(1,type); name = name+" "+to_string(x1)+" "+to_string(y1)+" "+to_string(x2)+" "+to_string(y2); QString name2= QString::fromStdString(name); QListWidgetItem * item = new QListWidgetItem(name2); ui->listWidget->addItem(item); } } file.close(); });
11.界面模块与计算模块的对接。详细地描述 UI 模块的设计与两个模块的对接,并在博客中截图实现的功能。
-
向ui模块载入core.dll
在ui.pro工程文件中加入core的头文件所在地址
INCLUDEPATH += E:\6wenming\qt_pros\pro4\core接着将core.dll复制到ui.exe所在的目录下
-
调用core.dll中的函数
在ui模块只使用了core.dll中的一个函数
int calInter(string path),这个函数的功能是传入一个文件的路径,然后这个函数从路径所在的文件中读取数据并计算交点,返回交点的个数
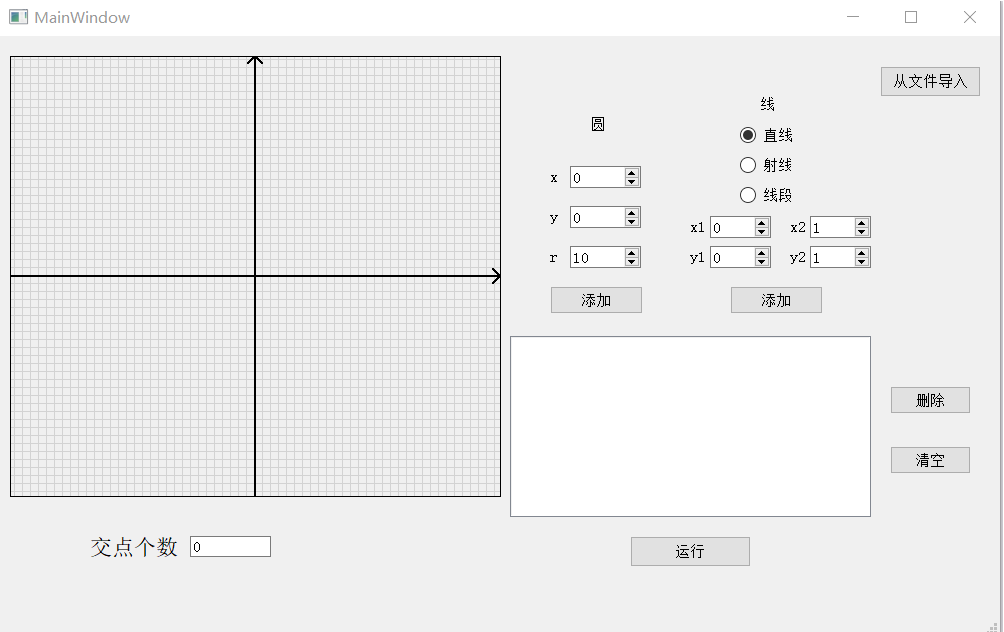
添加圆:
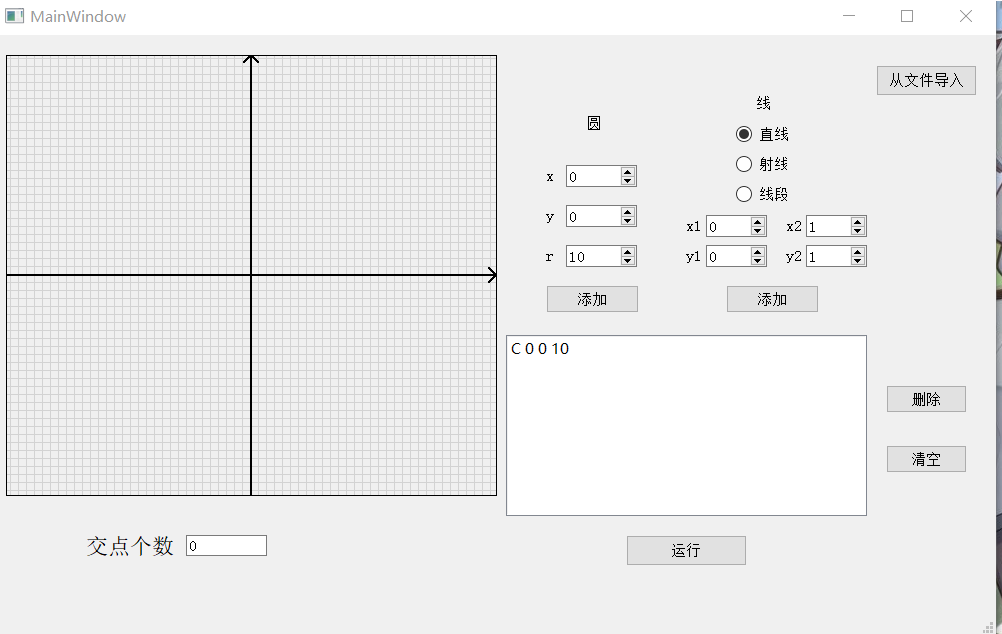
添加直线:
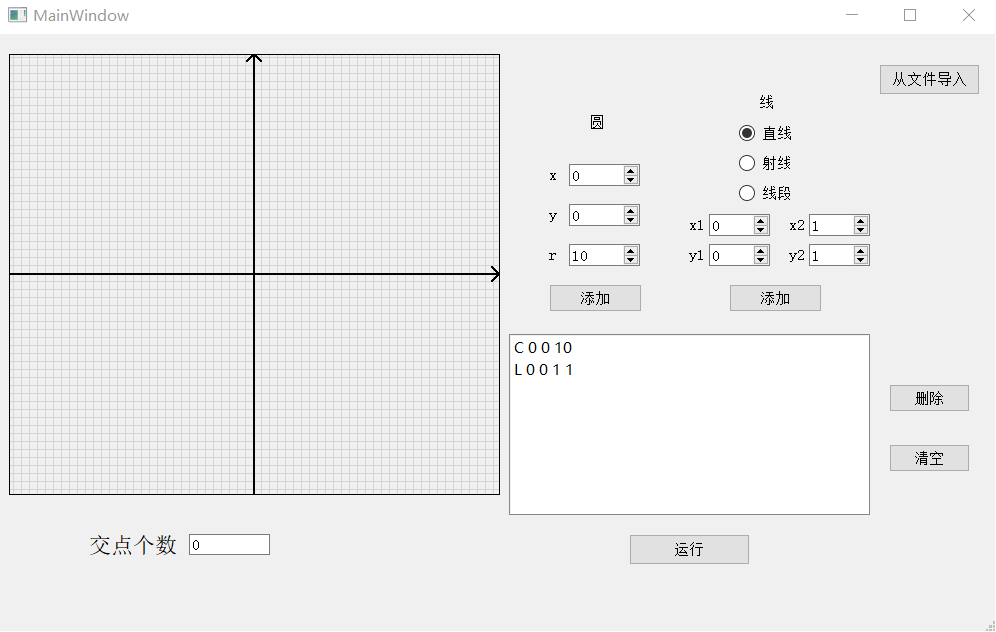
删除:
删除前:
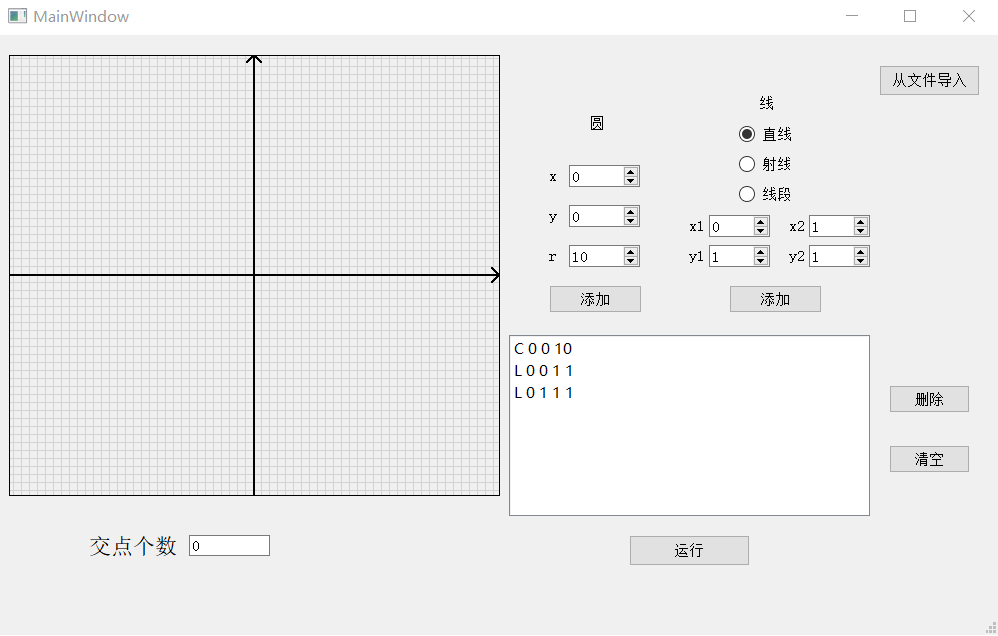
删除后(以删除第二项为例)
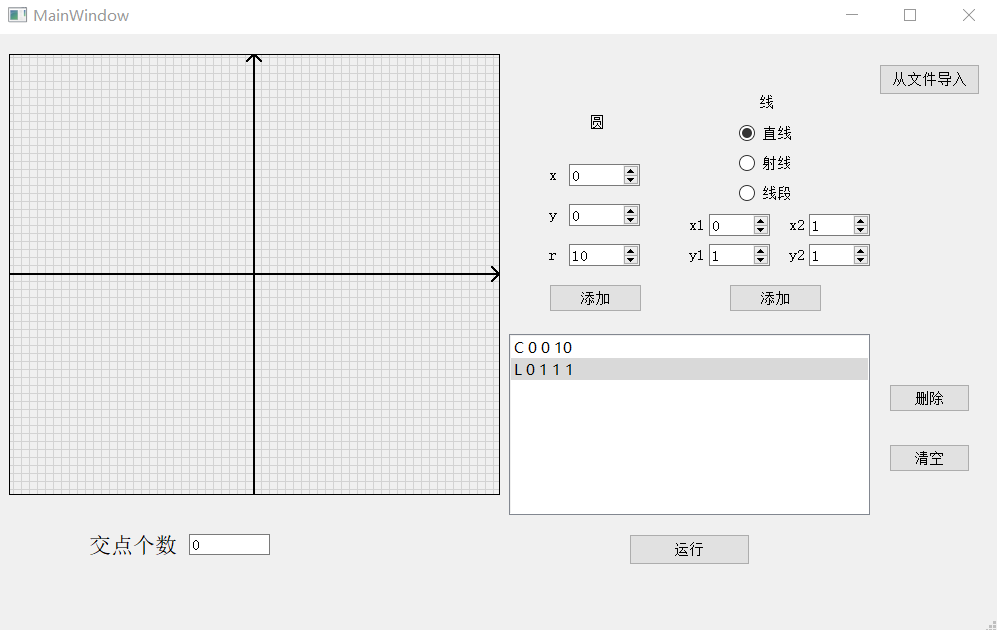
运行(绘制图,同时求交点)
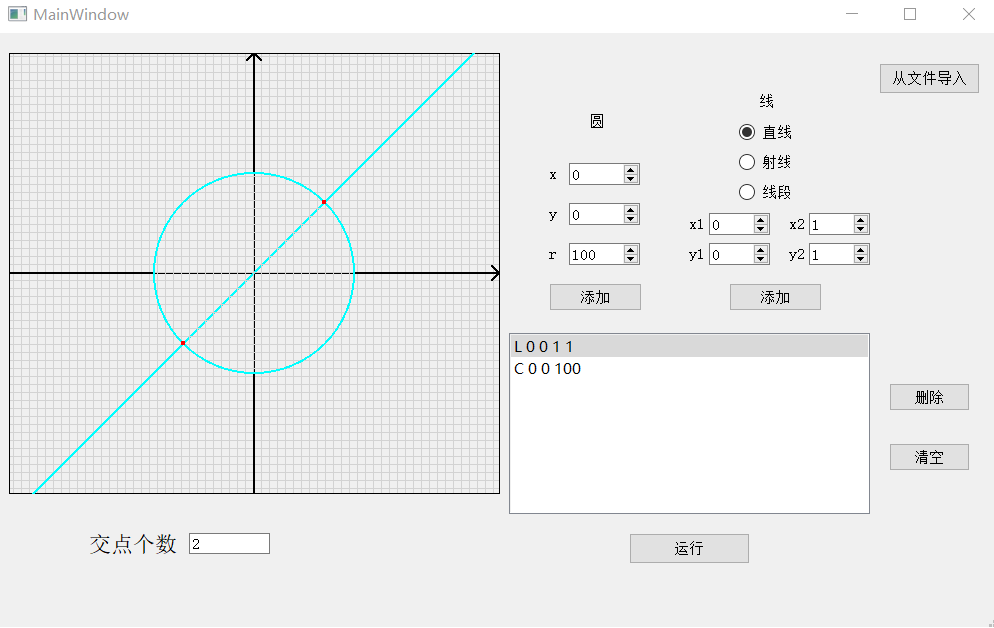
从文件导入:
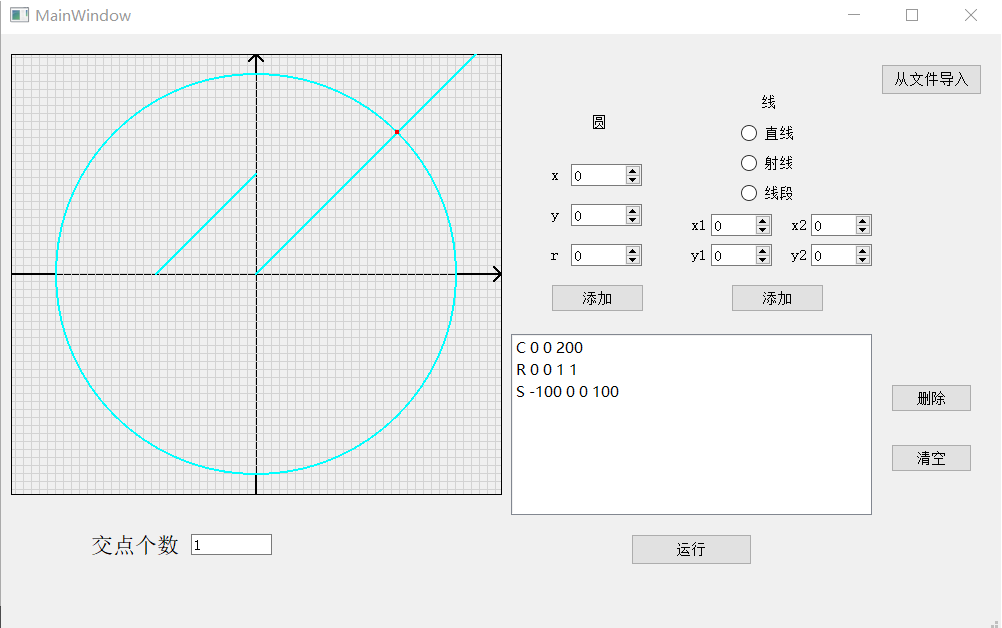
12.描述结对的过程,提供两人在讨论的结对图像资料(比如 Live Share 的截图)。关于如何远程进行结对参见作业最后的注意事项。
在结队编程中,我们使用了腾讯会议作为交流的平台,采用了其中一个人进行编程另外一个人进行监督的方式,但是,由于我们当中一个人比较擅长算法而另外一个人比较擅长ui方面的工作,所以在core方面是由队员1进行编程而队员2进行监督,在ui方面是由队员2进行编程而队员1进行监督
队员2监督队员1编写core的截图
队员1监督队员2的截图
13.看教科书和其它参考书,网站中关于结对编程的章节,例如:http://www.cnblogs.com/xinz/archive/2011/08/07/2130332.html ,说明结对编程的优点和缺点。同时描述结对的每一个人的优点和缺点在哪里(要列出至少三个优点和一个缺点)
结队编程:
优点:
- 可以取长补短,互相促进,配合的好会有1+1>2的效果
- 经验差距较大时,资深者可以起到引领和训练的作用,使另一方得到迅速提升
- 可以互相监督,互相鼓励,互相学习
缺点:
-
意见不合时由于没有第三方容易发生冲突
-
配合不好时严重影响编程甚至导致1+1<1
结队队员:
队员1
优点:
- 编程经验丰富,动手能力强
- 思路清晰,头脑敏捷
- 算法能力强
缺点:
ui经验不足
队员2:
优点:
-
知识量丰富
-
有ui设计经验
-
拖延较少,能按时完成任务
缺点:
- 编程能力欠缺
14.你实现完程序之后,在附录提供的PSP表格记录下你在程序的各个模块上实际花费的时间。
见文章开头处
附加题:
1.圆的部分完成
2.关于模块之间的松耦合
成员1: 17373015 博客地址: https://www.cnblogs.com/JordenQiao/
成员2: 17373260 博客地址https://www.cnblogs.com/i-love-ange-and-oo-forever/
成员3: 17373292 博客地址https://www.cnblogs.com/MountVoom/p/12558881.html
成员4: 17373287 博客地址https://www.cnblogs.com/miokun/p/12558605.html
代码地址1:https://github.com/prime21/IntersectProject
代码地址2:https://github.com/BUAA-SE/extremely-weak-GeoGebra
运行截图:
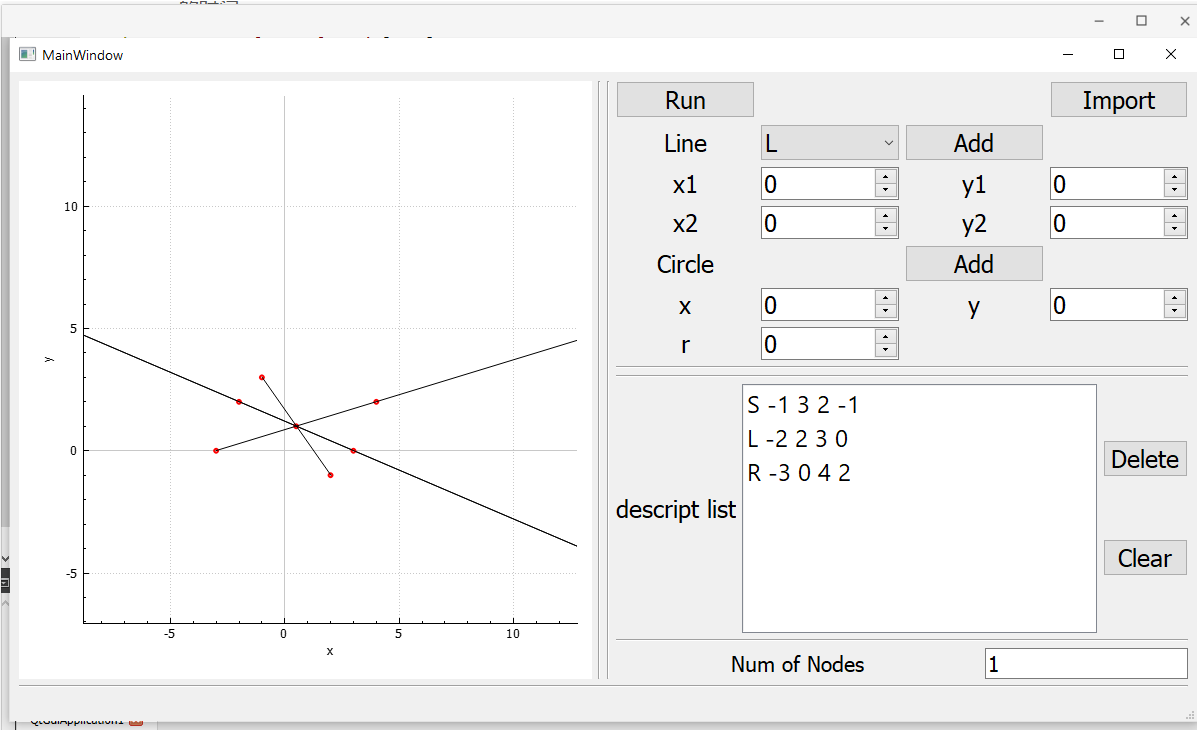
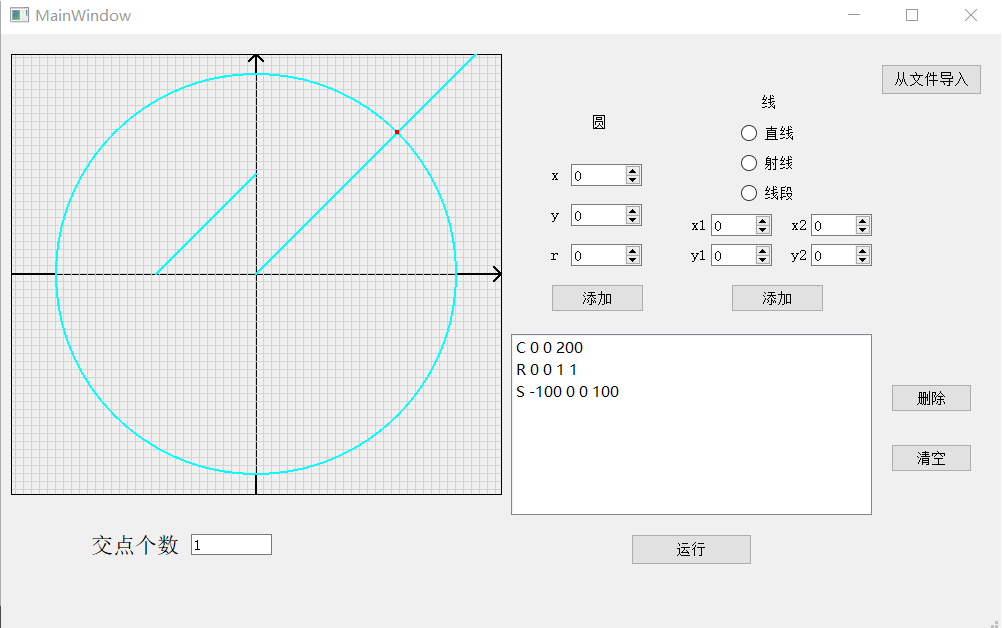
过程说明
在一开始的时候,我们的core因为采用了不同的结构以及不同的函数名等,导致如果更换了core则必须更改一些代码,所以我们对core进行了协商,决定通过归定一个相同名称的头文件以及同名函数的方法来实现松耦合.
我们都使用了一个相同的头文件calc.h,然后规定在其中有一个函数vector< pair<double, double> > count(vector<string> v)这个函数的参数为类似于"L 0 0 1 1"的string的vector,然后函数返回得到的交点,
靠着这个接口,我们实现了core和ui的松耦合,不需要更改ui或者core的代码,但是要注意,更换dll的同时应该更换头文件.



