矩阵游戏

4954: 矩阵游戏
时间限制(普通/Java):2000MS/6000MS 内存限制:65536KByte

描述

婷婷是个喜欢矩阵的小朋友,有一天她想用电脑生成一个巨大的n行m列的矩阵(你不用担心她如何存储)。她生成的这个矩阵满足一个神奇的性质：若用F[i][j]来表示矩阵中第i行第j列的元素，则F[i][j]满足下面的递推式:
F[1][1]=1
F[i,j]=aF[i][j-1]+b (j!=1)
F[i,1]=cF[i-1][m]+d (i!=1)
递推式中a,b,c,d都是给定的常数。
现在婷婷想知道F[n][m]的值是多少,请你帮助她。由于最终结果可能很大，你只需要输出F[n][m]除以1,000,000,007的余数。

输入

一行有六个整数n,m,a,b,c,d。意义如题所述。
1<=N,M<=10^1000 000,a<=a,b,c,d<=10^9

输出

包含一个整数，表示F[n][m]除以1,000,000,007的余数

样例输入

3 4 1 3 2 6

样例输出

85

思路
矩阵快速幂 加 费马小定理 缩小 n 和 m

每一行前一项 往 下一项变换的矩阵为

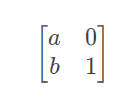
每一行 最后一项 往 下一行第一项 变化的矩阵为

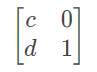
易得每行第一项向下一行第一项的变换的矩阵为

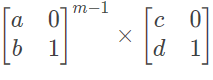
那第一行第一项往最后一行第一项变化的矩阵为

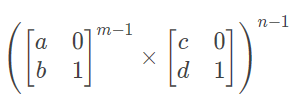
最后，最后一行第一项往最后一行最后一项变化的矩阵为

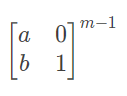
合起来就是

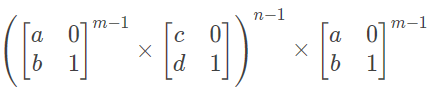
得出第一行第一项往最后一行最后一项的转移公式后，还需要缩小 n 和 m

矩阵乘法 也满足 费马小定理

在该定理中

当a!=1时，用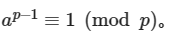这个公式

当a==1 时 用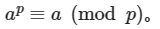这个公式

证明在这 https://oi-wiki.org/math/number-theory/fermat/

矩阵乘法也类似

这题用到的矩阵的[2][2]位置已经为1 所以需要判断[1][1]位置的数是否为 1

即 特判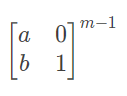 和 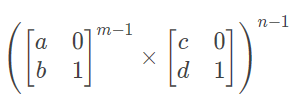的 [1][1]位置的数

因为矩阵只有两个位置的数有影响，我这里把矩阵压缩成两个数来计算，计算过程能更快

AC代码

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <bits/stdc++.h>
using namespace std;
long long t,w,p=1e9+7;

class Node
{
public:
    long long x,y;
}x,y,z;
long long Change(string s,long long mod)
{
    long long ans=0;
    int len=s.length();
    for(int i=0;i<len;i++)
        ans=(ans*10+s[i]-'0')%mod;
    return ans;
}
Node operator*(Node a,Node b)
{
    return(Node){a.x*b.x%p,(a.x*b.y+a.y)%p};
}
Node pow(Node a,long long b)
{
    Node ans=a;
    while(b)
    {
        if(b&1)ans=ans*a;
        a=a*a;
        b>>=1;
    }
    return ans;
}
void solve()
{
    long long n,m;
    long long a,b,c,d;
    string tn,tm;
    cin>>tn>>tm;
    cin>>a>>b>>c>>d;
    w=p-1+(a==1);
    m=Change(tm,w);
    x=pow(Node{a,b},m>1?m-2:m-2+w);
    y=Node{c,d};
    z=y*x;
    w=p-1+(z.x==1);
    n=Change(tn,w);
    z=pow(z,n>1?n-2:n-2+w);
    x=x*z;
    cout<<(x.x+x.y)%p<<endl;
}
signed main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int _;
    _=1;
//    cin>>_;
    while(_--)
    {
        solve();
    }
}

本文作者：Minza

本文链接：https://www.cnblogs.com/minz-io/p/17624191.html