1.线性模型的构成
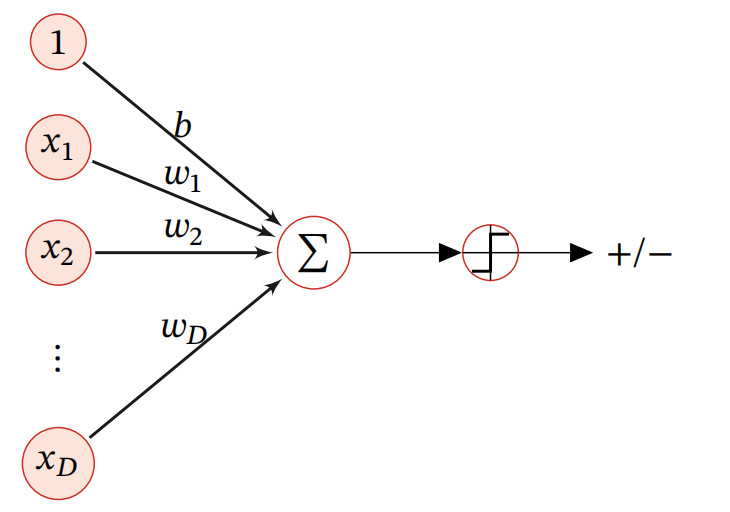
如下图所示,这是一个基础的线性模型示意图。
线性模型是机器学习中应用最广泛的模型,指通过样本特性的线性关系及组合来进行预测的模型,我们用下式来表示线性模型函数(判别函数)一般的表现形式:
\[\begin{gathered}
f\left( {\mathop x\limits^ \to ;\mathop \omega \limits^ \to ,b} \right) = {\omega _1}{x_1} + {\omega _2}{x_2} + \cdots + {\omega _D}{x_D} + b \\
= \mathop {{\omega ^T}}\limits^ \to \mathop x\limits^ \to + b \\
\end{gathered}\]
其中,\(\mathop x\limits^ \to = {\left[ {{x_1}, \cdots ,{x_D}} \right]^T}\)是D维的样本,\(\mathop \omega \limits^ \to = {\left[ {{\omega _1}, \cdots ,{\omega _D}} \right]^T}\)是\(D\)维的权重向量,\(b\)是偏置项,由于偏置项对整体来说不是主要影响因素,所以我们将整体线性模型函数表示为\({f\left( {\mathop x\limits^ \to ;\mathop \omega \limits^ \to } \right)}\)。
而在分类问题中,我们的输出的预计目标是离散的标签(定义为\(y\),即有\(y = f\left( {\mathop x\limits^ \to ;\mathop \omega \limits^ \to } \right)\)),而实际模型函数\({f\left( {\mathop x\limits^ \to ;\mathop \omega \limits^ \to } \right)}\)的输出是实数,所以我们无法直接使用模型函数的输出进行预测,所以需要引入一个非线性的决策函数(等价于激活函数的作用)\(g\left( \bullet \right)\)来预测模型真实输出,即\(y = g\left( {f\left( {\mathop x\limits^ \to ;\mathop \omega \limits^ \to } \right)} \right)\)。
2.线性判别函数、决策(等价与激活的作用)函数与决策边界
2.1二分类
在二分类模型中,\(y\)(我们预测所对比的标签)通常只有两类值,即负值和正值,我们用\(\left\{ {-1,+1} \right\}\)来表示(也可以用\(\left\{ {1,0} \right\}\)),而且线性判别函数我们只需要一个就能分出两个类别,即在特征空间中我们将所有满足\(f\left( {x;\omega } \right) = 0\)的点构成一个决策边界,以此实现分成两类的目的。
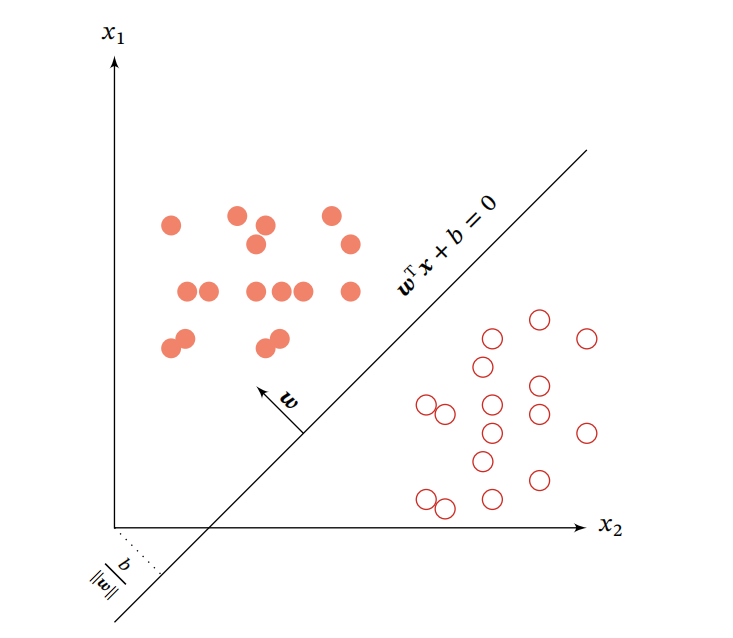
在特征空间中,决策平面与权重向量\(\omega\)正交。而且在特征空间的每个点距决策平面的有向距离用下式表示:
\[\gamma = \frac{{f\left( {\mathop x\limits^ \to ;\mathop \omega \limits^ \to } \right)}}{{\left\| {\mathop \omega \limits^ \to } \right\|}}
\]
其中\(\gamma\)表示点\({\mathop x\limits^ \to }\)在\({\mathop \omega\limits^ \to }\)方向上的投影,为了更加直观的看出这些效果,我们可以看到下图:
图中横纵坐标表示的是样本的特征向量\(\mathop x\limits^ \to = \left[ {{x_1},{x_2}} \right]\),权重向量\(\mathop \omega \limits^ \to = \left[ {{\omega _1},{\omega _2}} \right]\),假设总共为N个样本的训练集(包含数据和标签)\(D = \left\{ {\left( {\mathop {{x^{\left( n \right)}}}\limits^ \to ,{y^{\left( n \right)}}} \right)} \right\}_{n = 1}^N\),其中\({y^{\left( n \right)}} \in \left\{ { + 1, - 1} \right\}\),我们的线性模型要学到参数\(\mathop {{\omega ^ * }}\limits^ \to\),使得\(\mathop {{\omega ^ * }}\limits^ \to\)要满足\({y^{\left( n \right)}}f\left( {\mathop {{x^{\left( n \right)}}}\limits^ \to ;\mathop {{\omega ^ * }}\limits^ \to } \right) > 0,\forall n \in \left[ {1,N} \right]\),即线性判别函数为正的时候对应标签为正,同理,判别函数为负对应标签也为负。
那么问题来了,这个参数\(\mathop \omega \limits^ \to\)我们的模型是怎么学习到的呢?
这个问题的答案也就是各种分类问题不一样的答案,即我们是通过损失函数让线性预测模型学习参数\(\mathop \omega \limits^ \to\),损失函数的不同也是区分各种分类模型最明显的点。
二分类的损失函数是0-1损失函数,即:
\[{L_{01}}\left( {y,f\left( {\mathop x\limits^ \to ;\mathop \omega \limits^ \to } \right)} \right) = I\left( {yf\left( {\mathop x\limits^ \to ;\mathop \omega \limits^ \to } \right) > 0} \right)
\]
其中,\(I\left( \bullet \right)\)是指示函数,但是0-1损失函数的数学性质不好,其关于\(\mathop \omega \limits^ \to\)的导数为0,从而让其无法继续优化。
2.2多分类
多分类和二分类的区别主要有两个,第一,多分类的决策边界有多个(即,线性判别函数有多个);第二,各种分类问题的损失函数不同(即,模型学习参数\(\mathop \omega \limits^ \to\)的方式不同)。但是多分类与二分类又是紧密联系的,因为多分类问题可以拆分为多个二分类问题。
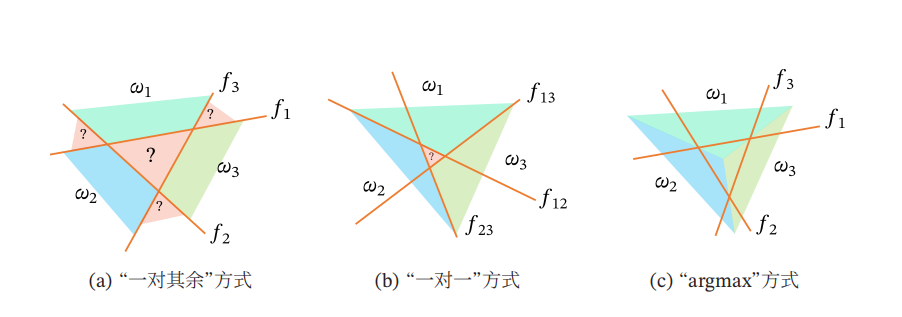
多分类问题类别为\(\left\{ {1,2, \cdots ,C} \right\}\),常用的有以下三类方式:
(1)“一对其余”方式:把多分类问题转换为C个“一对其余”的二分类问题。这种方式共需要C个判别函数,其中第c个判别函数\({f_c}\)是将类别c的样本和不属于该类别的样本分开。
(2)“一对一”方式:把多分类问题转换为\(C\left( {C - 1} \right)/2\)个“一对一”的二分类问题。这种方式共需要\(C\left( {C - 1} \right)/2\)个判别函数,其中第几个判别函数就是将第几个样本进行与其他样本的拆分。
(3)“argmax”方式:这是一种改进的“一对其余”方式,共需要C个判别函数:
\[{f_c}\left( {\mathop x\limits^ \to ,\mathop {{\omega _c}}\limits^ \to } \right) = \mathop {\omega _c^T}\limits^ \to \mathop x\limits^ \to + {b_c},c \in \left\{ {1, \cdots ,C} \right\}
\]
对于样本\({\mathop x\limits^ \to }\),如果存在一个类别c,相对于所有的其他类别\(\mathop c\limits^ \sim\)有\({f_c}\left( {\mathop x\limits^ \to ;\mathop {{\omega _c}}\limits^ \to } \right) > {f_{\mathop c\limits^ \sim }}\left( {\mathop x\limits^ \to ;\mathop {{\omega _{\mathop c\limits^ \sim }}}\limits^ \to } \right)\),那么\(\mathop x\limits^ \to\)属于类别c。该种方式的预测函数定义为:
\[y = \mathop {\arg \max }\limits_{c = 1}^C {f_c}\left( {\mathop x\limits^ \to ;\mathop {{\omega _c}}\limits^ \to } \right)
\]
如下图所示,其中“argmax”对比于其它两种方式具有明显的优势,因为它可以准确地判别任何一个样本所属的类别,而不会出现无法判别的问题。
3.Logistic回归(二分类方式)
说到Logistic回归我们首先来看一下Logistic函数的定义,Logistic函数是一种常用的S型函数,其定义式为:
\[\log istic\left( x \right) = \frac{L}{{1 + \exp \left( { - K\left( {x - {x_0}} \right)} \right)}}
\]
其中,\(\exp \left( \bullet \right)\)表示自然对数,\({{x_0}}\)是中心点,\(L\)是最大值,\(K\)是曲线的倾斜度,为了更加直观的看看logistic函数的性质,我们看看它的效果图:
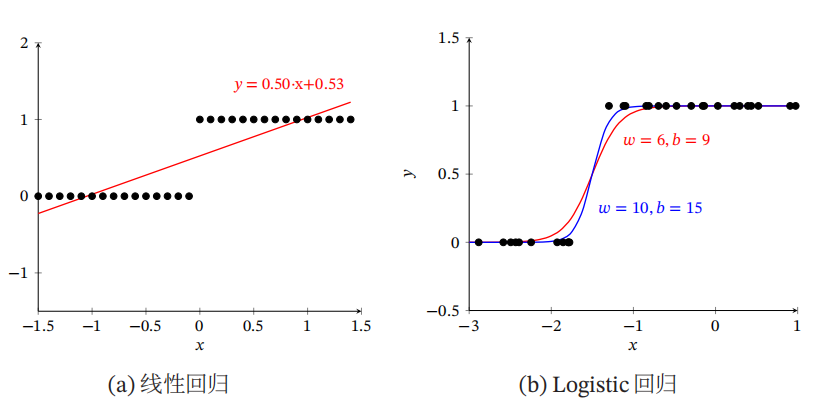
有上图我们可以看出,当x趋向于\(- \infty\)时,\(\log istic\left( x \right)\)趋向于0;当x趋向于\(+ \infty\)时,\(\log istic\left( x \right)\)趋向于L。并且当参数为第一行即蓝色实线时,\(\log istic\left( x \right)\)函数被称为标准\(\log istic\left( x \right)\)函数,记作\(\sigma \left( x \right)\)。且\(\sigma \left( x \right) = \frac{1}{{1 + \exp \left( { - x} \right)}}\)。
Logistic回归也就是对数回归,是一种常用的二分类问题的线性模型,为了解决连续的线性函数不适合进行分类的问题,我们定义对数回归为:
\[p\left( {y = 1|\mathop x\limits^ \to } \right) = g\left( {f\left( {\mathop x\limits^ \to ;\mathop \omega \limits^ \to } \right)} \right)
\]
其中,\(g\left( \bullet \right)\)称为激活函数,作用是将线性函数的值域从实数区间压缩到\(\left( {0,1} \right)\)之间,可以用来表示概率。
在Logistic回归中,我们使用Logistic函数来作为激活函数,标签y=1的后验概率为:
\[\begin{gathered}
p\left( {y = 1|\mathop x\limits^ \to } \right) = \sigma \left( {\mathop {{\omega ^T}}\limits^ \to \mathop x\limits^ \to } \right) \\
= \frac{1}{{1 + \exp \left( { - \mathop {{\omega ^T}}\limits^ \to \mathop x\limits^ \to } \right)}} \\
\end{gathered}\]
其中,\(\mathop x\limits^ \to = {\left[ {{x_1}, \cdots ,{x_D},1} \right]^T}\)表示样本的D+1维增广特征向量\(\mathop \omega \limits^ \to = {\left[ {{\omega _1}, \cdots ,{\omega _D},b} \right]^T}\)表示D+1维的增广权重向量。
既然得到了y=1的后验概率,那么在二分类中y=0的后验概率很容易就可以得到:
\[\begin{gathered}
p\left( {y = 0|\mathop x\limits^ \to } \right) = 1 - p\left( {y = 1|\mathop x\limits^ \to } \right) \hfill \\
= \frac{{\exp \left( { - \mathop {{\omega ^T}}\limits^ \to \mathop x\limits^ \to } \right)}}{{1 + \exp \left( { - \mathop {{\omega ^T}}\limits^ \to \mathop x\limits^ \to } \right)}} \hfill \\
\end{gathered}\]
而\({\mathop {{\omega ^T}}\limits^ \to \mathop x\limits^ \to }\)可以表示为:
\[\mathop {{\omega ^T}}\limits^ \to \mathop x\limits^ \to = \log \frac{{p\left( {y = 1|\mathop x\limits^ \to } \right)}}{{p\left( {y = 0|\mathop x\limits^ \to } \right)}}
\]
其中,\(\frac{{p\left( {y = 1|\mathop x\limits^ \to } \right)}}{{p\left( {y = 0|\mathop x\limits^ \to } \right)}}\)为样本正反例后验概率的比值,称为几率。
下图给出了线性回归和Logistic回归的区别:
3.1该种方式的参数学习
Logistic回归采用交叉熵作为损失函数,并使用梯度下降算法来进行参数的优化。
给定N个训练样本\(\left\{ {\mathop {{x^{\left( n \right)}}}\limits^ \to ,{y^{\left( n \right)}}} \right\}_{n = 1}^N\),用对数回归模型对每个样本进行预测,输出其标签为1的后验概率,记为\({{\hat y}^{\left( n \right)}}\),
\[{{\hat y}^{\left( n \right)}} = \sigma \left( {\mathop {{\omega ^T}}\limits^ \to {{\mathop x\limits^ \to }^{\left( n \right)}}} \right),1 \leqslant n \leqslant N
\]
由于\({y^{\left( n \right)}} \in \left\{ {0,1} \right\}\),样本\(\left( {\mathop {{x^{\left( n \right)}}}\limits^ \to ,{y^{\left( n \right)}}} \right)\)的真实条件概率可以表示为:
\[\begin{gathered}
{p_r}\left( {{y^{\left( n \right)}} = 1|\mathop {{x^{\left( n \right)}}}\limits^ \to } \right) = {y^{\left( n \right)}} \hfill \\
{p_r}\left( {{y^{\left( n \right)}} = 0|\mathop {{x^{\left( n \right)}}}\limits^ \to } \right) = 1 - {y^{\left( n \right)}} \hfill \\
\end{gathered}\]
使用交叉熵损失函数,但是为了简单起见,忽略了正则化项,其风险函数为:
\[\begin{gathered}
\Re \left( {\mathop \omega \limits^ \to } \right) = - \frac{1}{N}\sum\limits_{n = 1}^N {\left( {{p_r}\left( {{y^{\left( n \right)}} = 1|{{\mathop x\limits^ \to }^{\left( n \right)}}} \right)\log {{\hat y}^{\left( n \right)}} + {p_r}\left( {{y^{\left( n \right)}} = 0|{{\mathop x\limits^ \to }^{\left( n \right)}}} \right)\log \left( {1 - {{\hat y}^{\left( n \right)}}} \right)} \right)} \hfill \\
= - \frac{1}{N}\sum\limits_{n = 1}^N {\left( {{y^{\left( n \right)}}\log {{\hat y}^{\left( n \right)}} + \left( {1 - {y^{\left( n \right)}}} \right)\log \left( {1 - {{\hat y}^{\left( n \right)}}} \right)} \right)} \hfill \\
\end{gathered}\]
由风险函数\(\Re \left( {\mathop \omega \limits^ \to } \right)\)对参数\({\mathop \omega \limits^ \to }\)的偏导数为:
\[\begin{gathered}
\frac{{\partial \Re \left( {\mathop \omega \limits^ \to } \right)}}{{\partial \mathop \omega \limits^ \to }} = - \frac{1}{N}\sum\limits_{n = 1}^N {\left( {{y^{\left( n \right)}}\frac{{{{\hat y}^{\left( n \right)}}\left( {1 - {{\hat y}^{\left( n \right)}}} \right)}}{{{{\hat y}^{\left( n \right)}}}}{{\mathop x\limits^ \to }^{\left( n \right)}} - \left( {1 - {y^{\left( n \right)}}} \right)\frac{{{{\hat y}^{\left( n \right)}}\left( {1 - {{\hat y}^{\left( n \right)}}} \right)}}{{\left( {1 - {{\hat y}^{\left( n \right)}}} \right)}}{{\mathop x\limits^ \to }^{\left( n \right)}}} \right)} \hfill \\
= - \frac{1}{N}\sum\limits_{n = 1}^N {{{\mathop x\limits^ \to }^{\left( n \right)}}\left( {{y^{\left( n \right)}} - {{\hat y}^{\left( n \right)}}} \right)} \hfill \\
\end{gathered}\]
采用梯度下降算法,Logistic回归的训练过程为:初始化\(\mathop {{\omega _0}}\limits^ \to \leftarrow 0\),然后通过下式来迭代更新参数:
\[\mathop {{\omega _{t + 1}}}\limits^ \to \leftarrow \mathop {{\omega _t}}\limits^ \to + \alpha \frac{1}{N}\sum\limits_{n = 1}^N {{{\mathop x\limits^ \to }^{\left( n \right)}}\left( {{y^{\left( n \right)}} - \hat y_{{\omega _t}}^{\left( n \right)}} \right)}
\]
其中,\(\alpha\)是学习率,\({\hat y_{{\omega _t}}^{\left( n \right)}}\)是当参数为\(\mathop {{\omega _t}}\limits^ \to\)时,Logistic回归模型的输出。
4.Softmax回归(多分类的对数回归方式)
Softmax回归,是Logistic回归在多分类问题上的推广。
对于多分类问题,类别标签\(y \in \left\{ {1,2, \cdots ,C} \right\}\)可以有\(C\)个取值,给定一个样本\({\mathop x\limits^ \to }\),那么Softmax回归预测的属于类别c的条件概率为:
\[\begin{gathered}
p\left( {y = c|\mathop x\limits^ \to } \right) = soft\max \left( {\mathop {\omega _c^T}\limits^ \to \mathop x\limits^ \to } \right) \hfill \\
= \frac{{\exp \left( {\mathop {\omega _c^T}\limits^ \to \mathop x\limits^ \to } \right)}}{{\sum\nolimits_{c' = 1}^C {\exp \left( {\mathop {\omega _{c'}^T}\limits^ \to \mathop x\limits^ \to } \right)} }} \hfill \\
\end{gathered}\]
其中,\(\mathop {{\omega _c}}\limits^ \to\)是第c类的权重向量。
softmax回归的决策函数可以表示为:
\[\begin{gathered}
\hat y = \mathop {\arg \max }\limits_{c = 1}^C p\left( {y = c|\mathop x\limits^ \to } \right) \hfill \\
= \mathop {\arg \max }\limits_{c = 1}^C \left( {\mathop {\omega _c^T}\limits^ \to \mathop x\limits^ \to } \right) \hfill \\
\end{gathered}\]
与Logistic回归的关系表现为,当类别数C=2时,Softmax回归的决策函数为:
\[\begin{gathered}
\hat y = \mathop {\arg \max }\limits_{y \in \left\{ {0,1} \right\}} \left( {\mathop {{\omega _y}^T}\limits^ \to \mathop x\limits^ \to } \right) \hfill \\
= I\left( {\mathop {{\omega _1}^T}\limits^ \to \mathop x\limits^ \to - \mathop {{\omega _0}^T}\limits^ \to \mathop x\limits^ \to > 0} \right) \hfill \\
= I\left( {{{\left( {\mathop {{\omega _1}}\limits^ \to - \mathop {{\omega _0}}\limits^ \to } \right)}^T}\mathop x\limits^ \to > 0} \right) \hfill \\
\end{gathered}\]
其中,\(I\left( \bullet \right)\)是指示函数,所以根据二分类的线性模型我们可以得到权重向量的表达式为\(\mathop \omega \limits^ \to = \mathop {{\omega _1}}\limits^ \to - \mathop {{\omega _0}}\limits^ \to\)。
4.1参数学习
首先,我们都是通过损失函数使得我们的模型进行参数矩阵\(W\)学习的,而在softmax回归模型中我们使用的是交叉熵损失函数,所以我们可以得到其风险函数为:
\[\begin{gathered}
\Re \left( W \right) = - \frac{1}{N}\sum\limits_{n = 1}^N {\sum\limits_{c = 1}^C {{y_c}^{\left( n \right)}\log {{\hat y}_c}^{\left( n \right)}} } \hfill \\
= - \frac{1}{N}\sum\limits_{n = 1}^N {\left( {{{\left( {{y^{\left( n \right)}}} \right)}^T}\log {{\hat y}^{\left( n \right)}}} \right)} \hfill \\
\end{gathered}\]
其中,\({{\hat y}^{\left( n \right)}} = soft\max \left( {{W^T}\mathop {{x^{\left( n \right)}}}\limits^ \to } \right)\)为样本\({\mathop {{x^{\left( n \right)}}}\limits^ \to }\)在每个类别的后验概率。
风险函数\(\Re \left( W \right)\)关于W的梯度为:
\[\frac{{\partial \Re \left( W \right)}}{{\partial W}} = - \frac{1}{N}{\sum\limits_{n = 1}^N {\mathop {{x^{\left( n \right)}}}\limits^ \to \left( {{y^{\left( n \right)}} - {{\hat y}^{\left( n \right)}}} \right)} ^T}
\]
如果根据上式我们通过非向量形式转变,可以得到下列式子:
\[\frac{{\partial {L^{\left( n \right)}}\left( W \right)}}{{\partial W}} = - \mathop {{x^{\left( n \right)}}}\limits^ \to {\left( {{y^{\left( n \right)}} - {{\hat y}^{\left( n \right)}}} \right)^T}
\]
采用梯度下降法,softmax回归的训练过程为:初始化\({W_0} \leftarrow 0\),然后通过下式进行更新迭代:
\[\mathop {{W_{t + 1}}}\limits^ \to \leftarrow \mathop {{W_t}}\limits^ \to + \alpha \left( {\frac{1}{N}{{\sum\limits_{n = 1}^N {{{\mathop x\limits^ \to }^{\left( n \right)}}\left( {{y^{\left( n \right)}} - \hat y_{{W_t}}^{\left( n \right)}} \right)} }^T}} \right)
\]
其中\(\alpha\)是学习率,\({\hat y_{{W_t}}^{\left( n \right)}}\)是当参数为\(\mathop {{W_t}}\limits^ \to\)时,Softmax回归模型的输出。