排序算法之堆排序

堆排序

其他排序方法：选择排序、冒泡排序、归并排序、快速排序、插入排序、希尔排序、堆排序

概念

完全二叉树

在讲完全二叉树之前，先引入完美二叉树/满二叉树的概念。
每一个层的结点数都达到最大值的二叉树就叫完美二叉树。就像这样：

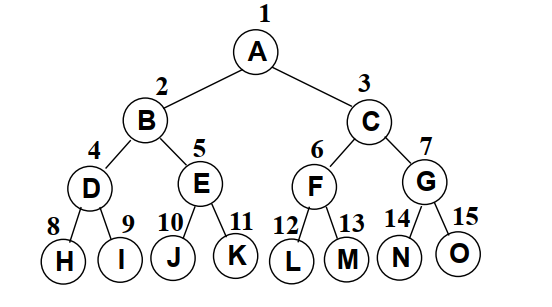
而完全二叉树的结点也像上图的满二叉树那样从上往下、从左到右进行编号的话，每个结点的位置都与满二叉树对应编号结点的位置相同。
也就是说，
如果最后一个叶子结点是其父亲的右儿子，则除了叶子结点，每个结点必定有两个儿子。
如果最后一个叶子结点是其父亲的左儿子，则除了其父亲与其它叶子结点，每个结点必定有两个儿子。

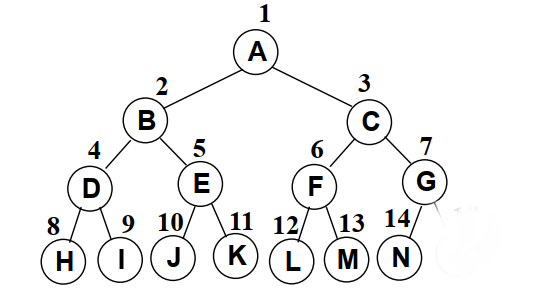
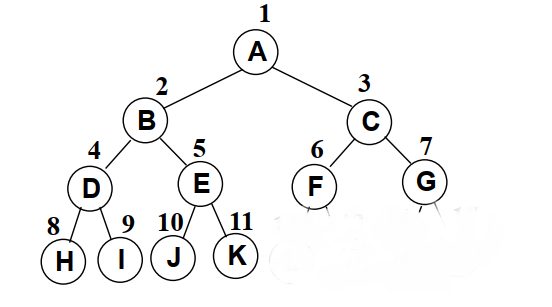
堆

堆是一个数组。它满足两个特点：

完全二叉树
任一结点的值都是其子树所有结点的最大值①或最小值②

情况①为最大堆

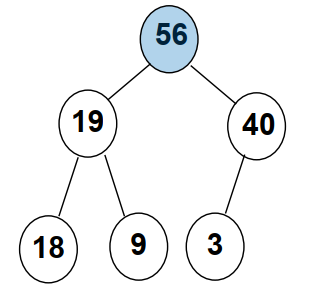
②为最小堆。

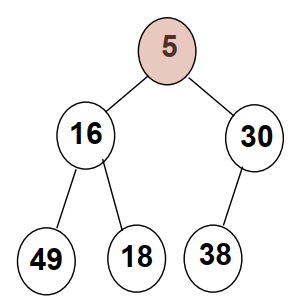
我们这里主要讲最大堆

存储结构

堆和完全二叉树我们通常用数组来存储，

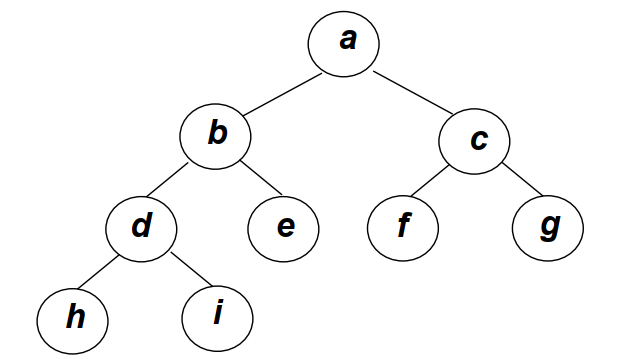
元素	a	b	c	d	e	f	g	h	i
下标	0	1	2	3	4	5	6	7	8

下标公式：
设父结点的下标为parent，左儿子的下标为leftChild，右儿子的下标为rightChild
$parent = (leftChild-1)/2$ 或 $\lfloor (rightChild-1)/2 \rfloor$
即，$$parent = \lfloor (child-1)/2 \rfloor$$

\[leftChild = parent*2+1 \]

\[rightChild = parent*2+2 \]

思想

堆排序其实就是利用堆的第二个特点：任一结点的值都是其子树所有结点的最大值或最小值。
只要将需要排序的数组建立成堆，然后每次取出根结点，就把剩下的结点调整成堆；再取出根结点，如此下去，最后便能得到排好序的数据。

性能

堆排序的性能比较复杂，我们先看堆的建立，堆的建立有两种方法：

将元素一个一个地插入到空堆里，时间复杂度为O(NlogN)
将元素按照完全二叉树的结构存放到数组里，然后再调整各结点的位置，时间复杂度为O(N)

建好堆之后，开始排序，排序也有两种方法：

取出根结点的元素，把元素放进临时的数组里，然后把剩下的结点调整成堆；重复前面的操作，最后临时数组里的数据便排好序了
直接在堆内部排序。先将根结点与最后一个结点的元素互换，然后将最后一个结点排除在外，进行堆调整；重复前面的操作，最后便排好序了

两种方法时间复杂度均为O(NlogN)，但第一种方法需要额外O(N)空间来进行辅助排序。

代码

# 建立最大堆
def buildMaxHeap(heap):
    # 最后一个结点的下标
    lastChild = len(heap) - 1
    # 最后一个结点的父结点的下标
    parent = lastChild - 1 >> 1
    # 从最后一个结点的父结点开始往前遍历结点
    # 并将以所遍历到的结点为根结点的堆调整为最大堆
    while parent >= 0:
        percDown(heap, parent, lastChild)
        parent -= 1

# 将堆调整为最大堆
# 需要调整的堆的最后一个结点下标为lastChild
# 需要调整的堆的根结点下标为root
# percolate:过滤、渗透
def percDown(heap, root, lastChild):
    if root < 0 or root >= lastChild: return

    key = heap[root]
    parent = root
    # 只要parent有儿子，就继续循环
    while parent << 1 < lastChild:
        # child指向parent的左儿子(parent*2+1)
        child = parent << 1 | 1
        # 如果右儿子比左儿子大，则child指向右儿子
        if child < lastChild and heap[child + 1] > heap[child]: child += 1

        # 如果根结点的值比儿子结点要小，则下滤
        if key < heap[child]:
            heap[parent] = heap[child]
        # 否则，位置适合，结束循环
        else:
            break
        # parent指向子结点，，调整以child为根的子堆
        parent = child
    # 如果发生了下滤，则将根结点的值移到合适的位置
    if parent != root:
        heap[parent] = key

# 返回最大堆的根结点元素，并将剩下结点调整为堆
def maxHeapPop(heap):
    # 最后一个结点的下标
    lastChild = len(heap) - 1

    if lastChild < 0: return

    # 取出根结点元素，将最后一个结点元素移到根结点
    maxItem, heap[0] = heap[0], heap[lastChild]
    # 堆元素少了一个
    lastChild -= 1
    heap.pop()

    # 将剩下结点调整为堆
    percDown(heap, 0, lastChild)

    return maxItem

方法一排序

# 堆排序
def heapSort1(heap):
    tmpHeap = heap.copy()
    # 建立最大堆
    buildMaxHeap(tmpHeap)
    # 取出根结点的元素，把元素放进临时的数组里，然后把剩下的结点调整成堆
    for i in range(len(heap) - 1, -1, -1):
        heap[i] = maxHeapPop(tmpHeap)

方法二排序

# 堆排序
def heapSort2(heap):
    # 建立最大堆
    buildMaxHeap(heap)
    # 最后一个结点的下标
    lastChild = len(heap) - 1
    # 将最大值与最后一个结点的元素位置互换，然后将最后一个结点排除在外，进行堆调整；一直重复这一步，直到只剩一个根结点
    while lastChild > 0:
        heap[0], heap[lastChild] = heap[lastChild], heap[0]
        lastChild -= 1
        percDown(heap, 0, lastChild)