平衡树学习笔记(二)splay
平衡树的基本思想:
普通的二叉搜索树会因为一些操作失去二叉搜索树的部分性质,而平衡树就是用一些额外的操作来保持二叉搜索树的性质。
一、节点维护的信息:
rt:根节点
tot:节点个数
fa[o]:父节点
ch[o][0/1]:左右子节点的编号
val[o]:节点权值
cnt[o]:权值出现的次数
sz[o]:子树大小
二、基本操作:
✧maintain(x):改变节点位置后,更新节点的sz[o]
tips:通常情况下,只需要maintain(x)和maintain(fa[x]),因为splay树的操作中一般只与x和fa[x]相关
✧get(x):判断节点x是父节点的左儿子还是右儿子
✧clear(x):删除点x
Code
void maintain(int x)
{
sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+cnt[x];
}
bool get(int x)
{
return x==ch[fa[x]][1];
}
void clear(int x)
{
ch[x][0]=ch[x][1]=sz[x]=fa[x]=val[x]=cnt[x]=0;
}
三、旋转操作rotate:
基本思想:为了使splay保持平衡而进行旋转操作,本质是将一个节点上移一个位置
/*
回想一下上一章二叉搜索树中,删除点时需要用子节点上移来代替该节点,就可以用于这个操作,还能使这个操作不再破坏二叉搜索树的平衡*/
旋转的前提:
(1)保证整棵splay的中序遍历不变(保持其平衡性质)
(2)保证所有点在改变位置之后维护的信息依然正确且有效
(3)root必须指向旋转之后得到的根节点
旋转分为两种:左旋和右旋
右旋:将节点x的左节点向上移一个位置,用以取代x
左旋:将节点x的右节点向上移一个位置,用以取代x
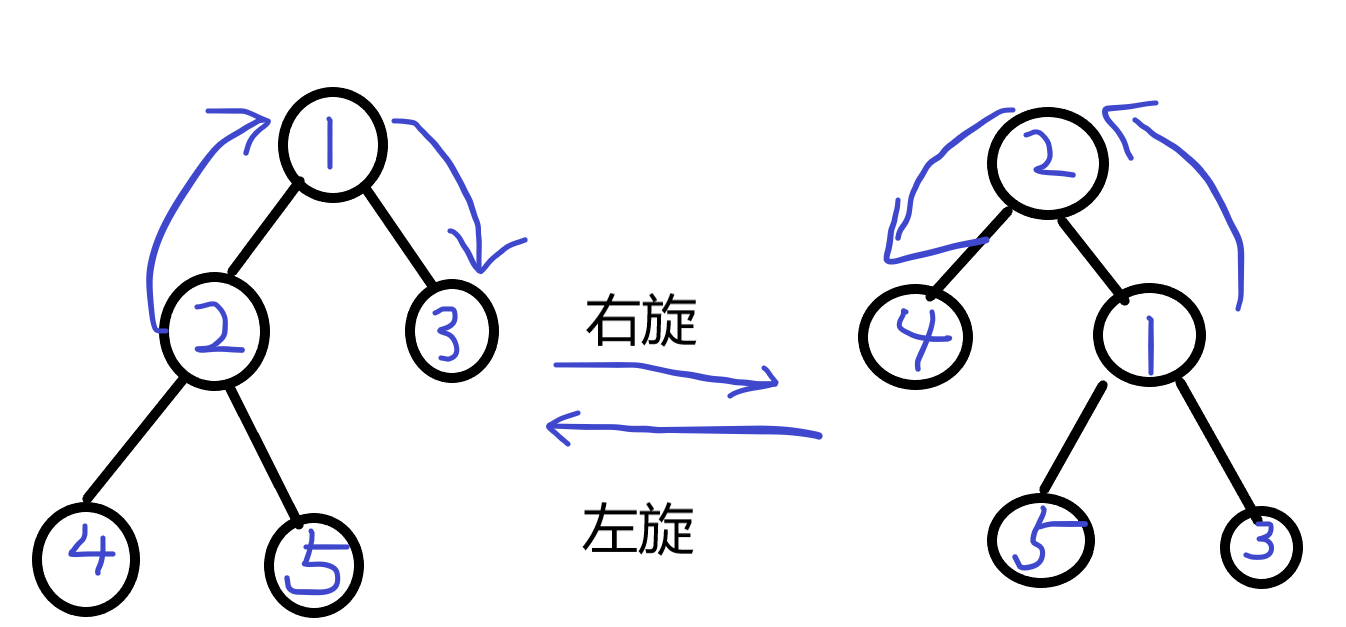
依旧使分类讨论完成旋转操作:
设要旋转的节点为x,其父节点为y
(1)若x为y的右儿子:
<1>将y的左儿子指向x的右儿子(如果x有右儿子),将x的右儿子的父亲指向y
<2>将x的右儿子指向y,将y的父亲指向x
<3>若原先的y有父节点z,则将x的父节点指向z,将z的y原先的节点位置指向x
(2)若x为y的左儿子:
<1>将y的右儿子指向x的左儿子(如果x有左儿子),将x的左儿子的父亲指向y
<2>将x的左儿子指向y,将y的父亲指向x
<3>若原先的y的父节点z,则将x的父节点指向z,将z的y的原先的节点位置指向x
经过观察,很容易发现,两种情况可以合为一种写法
还记得之前的get()操作吗,这里就可以用这个操作来用xor完成左右节点的左右横跳变化
那么就来描述一下合并两种情况之后的rotate:
op1:将x的一个子节点变为y的一个子节点
op2:将y变为x的子节点
tips:
op3:将y原先的父节点变为x的父节点
Code
void rotate(int x)
{
int y=fa[x],z=fa[y],chk=get(x);
ch[y][chk]=ch[x][chk^1];
if(ch[x][chk^1]) fa[ch[x][chk^1]]=y;
ch[x][chk^1]=y;
fa[y]=x;
fa[x]=z;
if(z) ch[z][y==ch[z][1]]=x;
maintain(y);
maintain(x);//这里一定要先更新y再更新x,因为此时y是x的子节点,y的所有量都会影响x
}
tips:很显然,rotate有以下性质:
<1>无论左旋还是右旋,都可以发现,rotate(x)之后,x的与x类型(指是左节点还是右节点)相同的子节点,仍为x的子节点,且该节点的节点类型不变。
<2>左旋或右旋之后,x的与x类型不同的子节点成为了原先x的父节点y的子节点,且节点类型发生了改变(如右旋之后,x的右儿子变成了y的左儿子)。
有一个记忆技巧就是:x的外侧节点不变,内侧节点变为y
三、伸展操作splay:
基本思想:每访问一个节点x后都要将其旋转到根节点
除了maintain、clear、get操作,其他的操作,每一次都要将最终答案splay到根节点
分为6种情况,但是由于rotate的分类方式,所以splay也可以用一个函数处理六种情况
具体内容可以去往OIWIKI
大意就是:
(1)若x的父节点为根节点,则直接左旋或右旋一次x即可
(2)若x的父节点不为根节点。
<1>若x的类型与x的父节点相同,则先将其父亲左旋或右旋,再将x左旋或右旋。
<2>若x的类型与x的父节点不同,则直接两次左旋或右旋x即可。
Code
void splay(int x)
{
for(int f=fa[x];f=fa[x],f;rotate(x))
if(fa[f]) rotate(get(x)==get(f) ? f : x);
rt=x;
}
简单想一下就会发现这个写法很完美地包含了上面六种情况。
由于x一定会被上旋一次,因此需要讨论的问题只有第一次是上旋fa[x]还是上旋x。
✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧
以下的操作一定要记住一点:splay具有全部二叉搜索树的性质
五、插入元素操作insert:
不说了,还是分情况讨论:
(1)整个树为空,新建根节点就完事了,不需要splay
(2)树不为空,则从节点向下找。
✧✧✧✧✧<1>找到k,则修改节点信息,splay即可
✧✧✧✧✧<2>如果k不存在,则新建一个点,splay
Code
void insert(int k)
{
if(!rt)
{
cnt[++tot]=1;
val[tot]=1;
rt=tot;
maintain(tot);
return;
}
while(1)
{
int cur=rt,f=0;
if(val[cur]==k)
{
cnt[cur]++;
maintain(cur);
maintain(cur);
maintain(f);
splay(x);
return;
}
f=cur;
cur=ch[f][val[cur]<k];
if(!cur)
{
val[++tot]=k;
cnt[tot]=1;
fa[tot]=f;
ch[f][val[f]<k]=tot;
maintain(tot);
maintain(f);
splay(tot);
}
if(!cur)
}
}
六、查询k的排名:
灵活运用二叉搜索树的性质即可:
k的排名的定义:严格小于k的数的数量+1
Code
int queryrk(int k)
{
int res=0,cur=rt;
while(1)
{
if(k<val[cur]) cur=ch[cur][0];
else
{
res+=sz[ch[cur][0]];
if(val[cur]==k)
{
splay(cur);
return res+1;
}
res+=cnt[cur];
cur=ch[cur][1];
}
}
}
和上一个操作差不多,不过有时候会出现k并不存在与平衡树中的情况。
此时如果直接查询就会RE。
所以我们有两种解决方式:
(1)把函数写法改成不需要严格相等
(2)先insert(x),然后查询,再del(x)。(这里借用了查询前驱的技巧,和删除操作,这两个操作都会在后面被提及)
六、查询排名为k的数:
啊又是二叉搜索树性质的运用
排名吗,不会出现什么太奇怪的问题。
但是要保证k<=tot,否则肯定无解。
Code
int kth(int k)
{
int cur=rt;
while(1)
{
if(k<=sz[ch[cur][0]]) cur=ch[cur][0];
else
{
k-=cnt[cur]+sz[ch[cur][0];
if(k<=0)
{
splay(cur);
return val[cur];
}
cur=sz[ch[cur][1]];
}
}
}
七、查询x的前驱:
前驱的定义:小于x的最大的数
因此根据定义,x的前驱是x的左子树的右链顶点。
查询前驱之前需要先insert(x),然后再找到x左子树的右链顶点,最后del(x)删除x。
tips1:函数返回的是x的前驱所在的点的编号
tips2:如果不存在x的前驱,函数pre()会返回0,因此无解也不会出现RE的情况
Code
int pre()
{
int cur=ch[rt][0];
if(!cur) return cur;
while(ch[cur][1]) cur=ch[cur][1];
splay(cur);
return cur;
}
八、查询x的后继:
和上面完全同理
后继的定义:大于x的最小的数
直接insert(x),找到x的右子树的左链顶点,然后del(x)即可。
int nxt()
{
int cur=ch[rt][1];
if(!cur) return cur;
while(ch[cur][1]) cur=ch[cur][1];
splay(cur);
return cur;
}
九、合并两棵splay树:
设两棵树的根节点分别为x,y,在合并操作中,规定x树中的最大值小于y树中的最小值。(维护splay树的性质)
(1)若其中一棵树为空树或者两棵树都是空树,那么直接设rt=非空的树的根或者rt=0即可
(2)若两棵树均不为空树,则将x的最大值splay到根,将x的右子树设置成y并更新节点信息,最终返回节点x即可。
tips:合并操作中"x树中的最大值小于y树中的最小值"是合并的前提条件,而不是因为上述操作而成立的。
因此合并操作之前需要已知上述条件成立,或者通过重构或者其他操作使得上述条件成立。
十、删除x的操作:
这不是一个核心操作,确实最难写的操作
步骤:
(1)将k splay到根(进行该操作后val[rt]==k)
(2)判断cnt[k]:
✧✧✧✧✧<1>若cnt[k]>1,直接cnt[k]--即可
✧✧✧✧✧<2>若cnt[k]=1,分情况讨论,合并rt的两棵子树
✧✧✧✧✧✧✧✧✧✧{1}左右子树均为空树,clear(rt)
✧✧✧✧✧✧✧✧✧✧{2}左右子树中有一棵子树为空树:clear(rt),rt=ch[rt][1/0]
✧✧✧✧✧✧✧✧✧✧{3}左右子树均不为空树:由于这两棵子树是rt的左右子树,一定满足合并两颗splay的条件,因此按上述操作合并即可
Code
void del(int k)
{
queryrnk(k);
if(cnt[rt]>1)
{
cnt[rt]--;
maintain(rt);
return;
}
if(!ch[rt][0] && !ch[rt][1])
{
clear(rt);
rt=0;
return;
}
if(!ch[rt][1])
{
int cur=rt;
rt=ch[rt][0];
fa[rt]=0;
clear(cur);
return;
}
if(!ch[rt][0])
{
int cur=rt;
rt=ch[rt][1];
fa[rt]=0;
clear(cur);
return;
}
int cur=rt,x=pre();//此时k在根节点的位置上,找pre()找到的是rt的左子树中的最大值
fa[ch[cur][1]]=x;
ch[x][1]=ch[cur][1];
clear(cur);
maintain(cur);
}
✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧✧
完结撒花!
才没完事呢!
让我们把代码合起来:
来几道题:https://www.luogu.com.cn/problem/P6136
其实和普通平衡树没什么关系,只是强制在线卡其他奇怪的离线做法。
题解代码
Code
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+1e5+50;
int fa[maxn],sz[maxn],ch[maxn][4],tot,val[maxn],cnt[maxn],rt;
void maintain(int x)
{
sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+cnt[x];
}
bool get(int x)
{
return ch[fa[x]][1]==x;
}
void clear(int x)
{
sz[x]=fa[x]=ch[x][0]=ch[x][1]=val[x]=cnt[x]=0;
}
void rotate(int x)
{
int y=fa[x],z=fa[y],chk=get(x);
ch[y][chk]=ch[x][chk^1];
if(ch[x][chk^1]) fa[ch[x][chk^1]]=y;
ch[x][chk^1]=y;
fa[x]=z;
fa[y]=x;
if(z) ch[z][ch[z][1]==y]=x;
maintain(y);
maintain(x);
}
void splay(int x)
{
for(int f=fa[x];f=fa[x],f;rotate(x))
{
if(fa[f]) rotate(get(x)==get(f) ? f : x);
}
rt=x;
}
void insert(int k)
{
if(!rt)
{
cnt[++tot]=1;
val[tot]=k;
rt=tot;
maintain(rt);
return;
}
int f=0,cur=rt;
while(1)
{
if(val[cur]==k)
{
cnt[cur]++;
maintain(cur);
maintain(f);
splay(cur);
break;
}
f=cur;
cur=ch[cur][val[cur]<k];
if(!cur)
{
fa[++tot]=f;
ch[f][val[f]<k]=tot;
cnt[tot]=1;
val[tot]=k;
maintain(tot);
maintain(f);
splay(tot);
break;
}
}
}
int queryrnk(int k)
{
int res=0,cur=rt;
while(1)
{
if(k<val[cur]) cur=ch[cur][0];
else
{
res+=sz[ch[cur][0]];
if(k==val[cur])
{
splay(cur);
return res+1;
}
res+=cnt[cur];
cur=ch[cur][1];
}
}
}
int kth(int k)
{
int cur=rt;
while(1)
{
if(k<=sz[ch[cur][0]])
{
cur=ch[cur][0];
}
else
{
k-=cnt[cur]+sz[ch[cur][0]];
if(k<=0)
{
splay(cur);
return val[cur];
}
cur=ch[cur][1];
}
}
}
int pre()
{
int cur=ch[rt][0];
if(!cur) return cur;
while(ch[cur][1]) cur=ch[cur][1];
splay(cur);
return cur;
}
int nxt()
{
int cur=ch[rt][1];
if(!cur) return cur;
while(ch[cur][0]) cur=ch[cur][0];
splay(cur);
return cur;
}
void del(int k)
{
queryrnk(k);
if(cnt[rt]>1)
{
cnt[rt]--;
maintain(rt);
return;
}
if(!ch[rt][0] && !ch[rt][1])
{
clear(rt);
rt=0;
return;
}
if(!ch[rt][0])
{
int cur=rt;
rt=ch[rt][1];
fa[rt]=0;
clear(cur);
return;
}
if(!ch[rt][1])
{
int cur=rt;
rt=ch[rt][0];
fa[rt]=0;
clear(cur);
return;
}
int cur=rt,x=pre();
fa[ch[cur][1]]=x;
ch[x][1]=ch[cur][1];
clear(cur);
maintain(rt);
}
int main()
{
// freopen("splay.in","r",stdin);
// freopen("splay.out","w",stdout);
int n,m,last=0,sum=0;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i)
{
int x;
scanf("%d",&x);
insert(x);
}
for(int i=1;i<=m;++i)
{
int opt,x;
scanf("%d%d",&opt,&x);
x^=last;
if(opt==1) insert(x);
if(opt==2) del(x);
if(opt==3)
{
insert(x);
last=queryrnk(x);
del(x);
sum^=last;
}
if(opt==4)
{
last=kth(x);
sum^=last;
}
if(opt==5)
{
insert(x);
last=val[pre()];
sum^=last;
del(x);
}
if(opt==6)
{
insert(x);
last=val[nxt()];
sum^=last;
del(x);
}
}
printf("%d",sum);
return 0;
}
这次真的结束了。BYE~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号