YBTOJ 路径求和
题面:
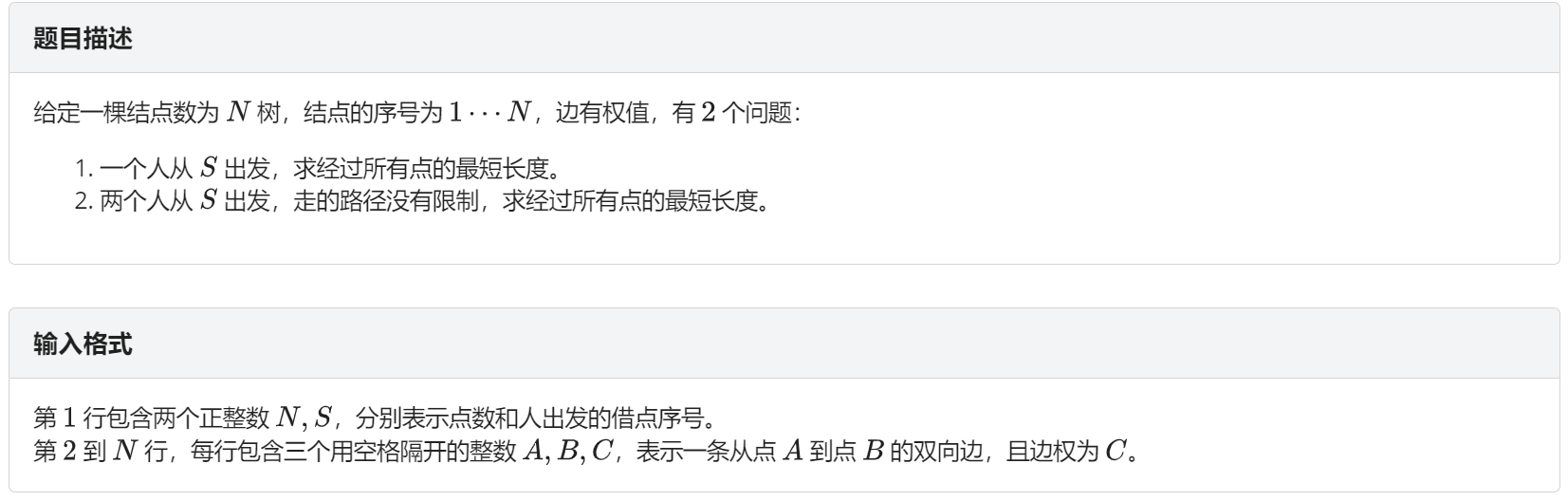
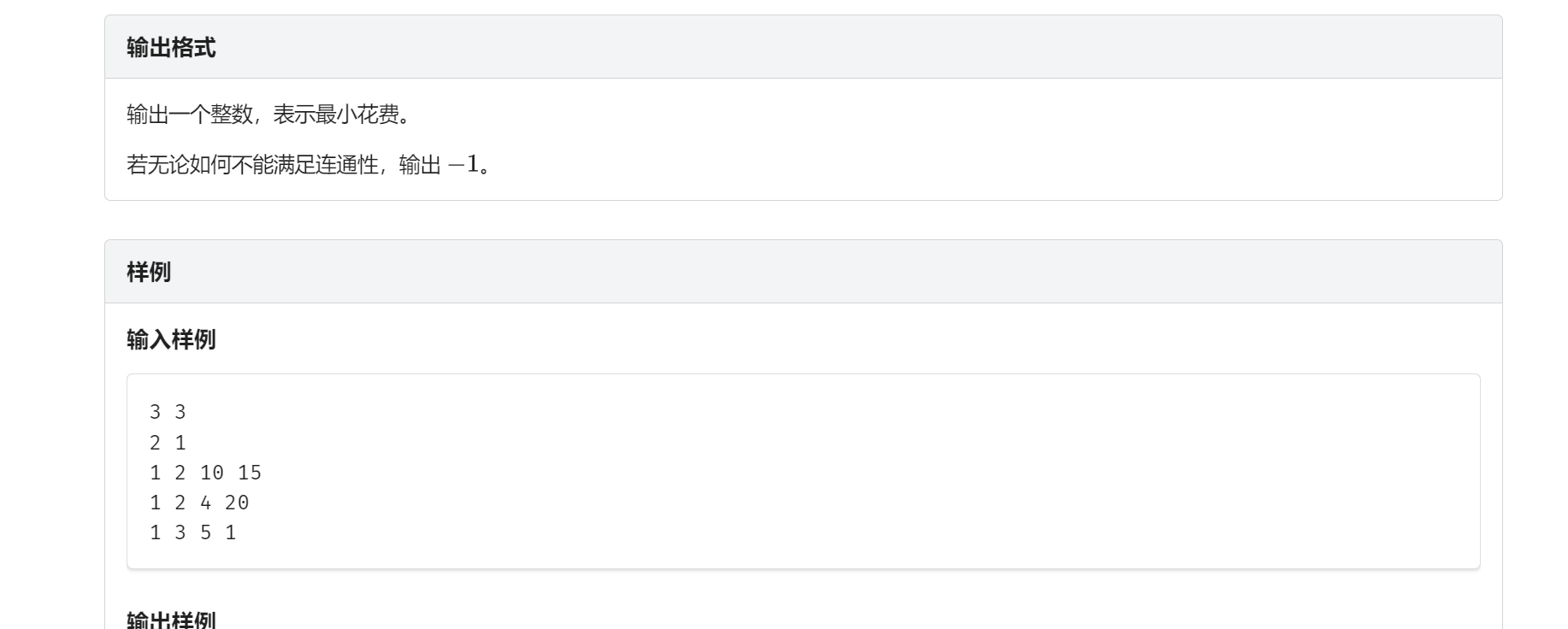
题目分析:
考虑每一条边对于答案的贡献,根据树的性质,每一条边一定将整棵树分成了两个子树,而该边的贡献=子树1中叶节点数子树2中节点总数+子树2中叶节点数子树1中节点总数。
由于树有一个重要性质:
树的任意一个点都可以作为树的根
然后?没了。
哦不是,还有一个重要的点:
要注意乘法算式过程中的点要尽量多开long long,因为会爆int
#include<bits/stdc++.h>
using namespace std;
const int maxn=5e5+100;
int head[maxn],ecnt=-1,m,a,b,c,du[maxn],root;
long long ans;
long long leaf[maxn],tot[maxn],n,totleaf;
struct mint
{
int nxt,v,w;
}e[maxn<<1];
inline void addline(int u,int v,int w)
{
e[++ecnt].nxt=head[u];
e[ecnt].v=v;
e[ecnt].w=w;
head[u]=ecnt;
}
void dfs(int now,int fa)
{
tot[now]=1;
if(du[now]==1)
{
totleaf++;
leaf[now]=1;
}
for(int i=head[now];~i;i=e[i].nxt)
{
int v=e[i].v;
if(v==fa) continue;
dfs(v,now);
leaf[now]+=leaf[v];
tot[now]+=tot[v];
}
return;
}
void find(int now,int fa)
{
for(int i=head[now];~i;i=e[i].nxt)
{
int v=e[i].v;
if(v==fa) continue;
find(v,now);
ans+=(long long)e[i].w*(leaf[v]*(n-tot[v])+tot[v]*(totleaf-leaf[v]));
}
}
int main()
{
memset(head,-1,sizeof(head));
scanf("%lld%d",&n,&m);
for(int i=1;i<=m;++i)
{
scanf("%d%d%d",&a,&b,&c);
du[c]++;
du[b]++;
addline(b,c,a);
addline(c,b,a);
}
dfs(1,0);
find(1,0);
printf("%lld",ans);
return 0;
}



