Lucas卢卡斯定理模板

题目算法要素：组合数学&线性求逆元&线性求阶乘的逆元&Lucas定理

题面：

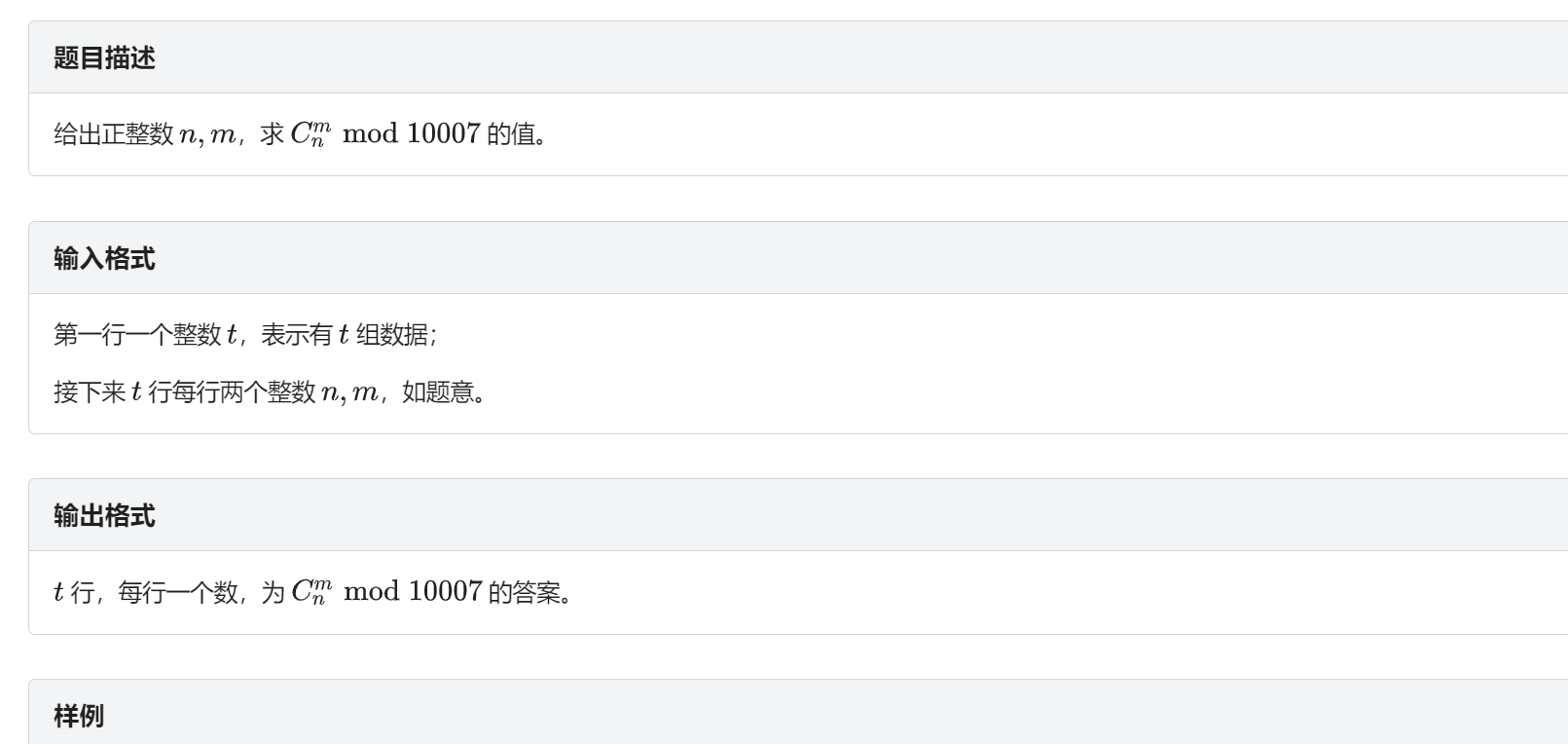
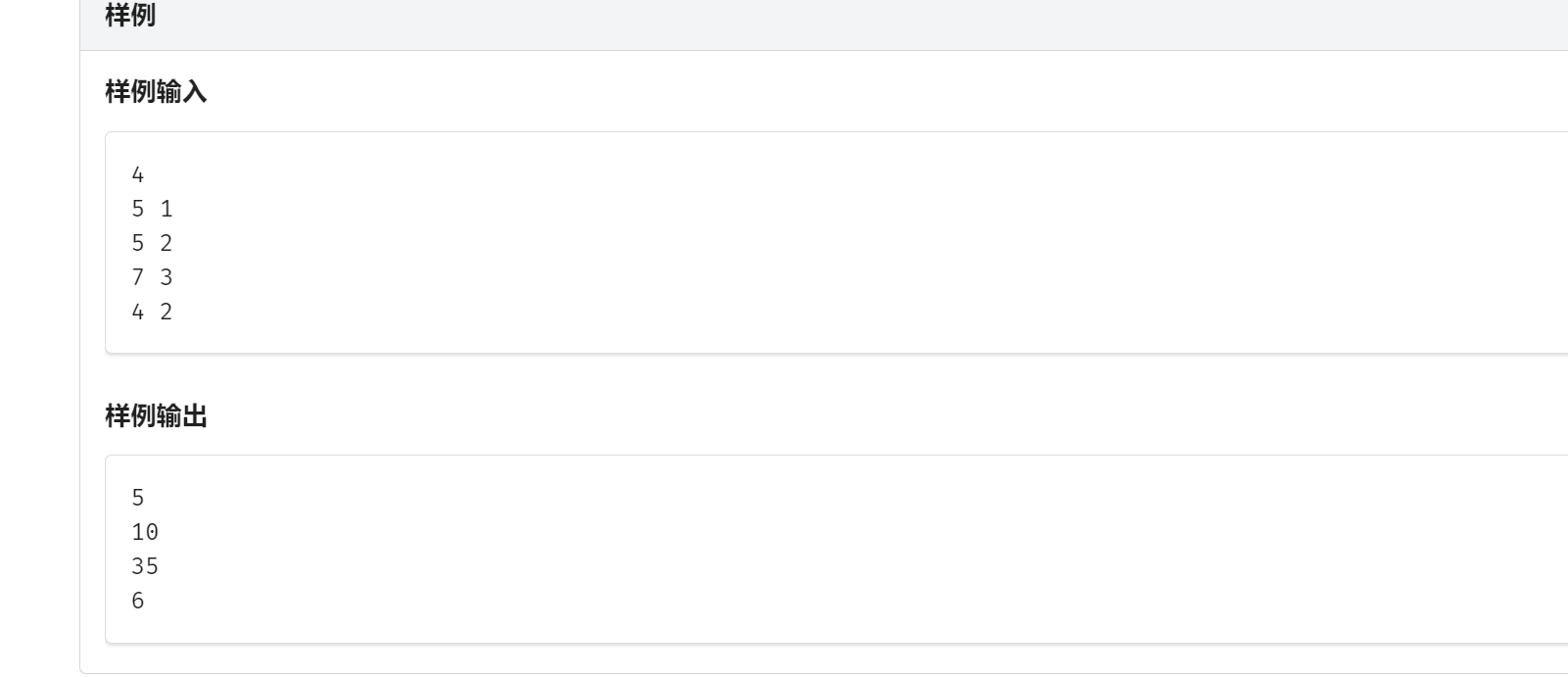
Lucas定理内容：不会的走传送门去oiwiki

分析：

由于这题n、m较大，因此直接硬算肯定会炸（阶乘都算不完）。
故使用Lucas定理加速。
为了减少计算量，先预处理出模mod下的阶乘、和阶乘逆元。

线性求逆元：inv[i]表示i在模mod意义下的乘法逆元

inv[0]=inv[1]=1;
for(int i=2;i<=n;++i) inv[i]=((mod-mod/i*inv[mod%i])%mod+mod)%mod;

线性求阶乘的逆元：facinv[i]表示i的阶乘在模mod意义下的乘法逆元

facinv[0]=facinv[1]=1;
for(int i=2;i<=n;++i) facinv[i]=facinv[i-1]*inv[i]%mod;

Code

完整代码

#include<bits/stdc++.h>
using namespace std;
const int mod=10007;
long long n,m;
int t;
long long fac[10060],inv[10060],facinv[10060];
void init()
{
	inv[0]=inv[1]=1;
	fac[0]=fac[1]=1;
	facinv[0]=facinv[1]=1;
	for(int i=2;i<=10007;++i) inv[i]=((mod-mod/i*inv[mod%i])%mod+mod)%mod;
	for(int i=2;i<=10007;++i) fac[i]=fac[i-1]%mod*i%mod;
	for(int i=2;i<=10007;++i) facinv[i]=facinv[i-1]*inv[i]%mod;	
}
long long C(long long m,long long n)
{
	if(n<m) return 0;
	return fac[n]%mod*facinv[m]%mod*facinv[n-m]%mod;
}	
long long Lucas(long long m,long long n)
{
	if(m==0) return 1;
	return 	C(m%mod,n%mod)%mod*Lucas(m/mod,n/mod)%mod;
}
int main() 
{
	scanf("%d",&t);
	init();
	for(int q=1;q<=t;++q)
	{
		scanf("%lld%lld",&n,&m);
		long long ans=Lucas(m,n);
		printf("%lld\n",ans);	
	}
	return 0;
}