YBTOJ 数独游戏
题面
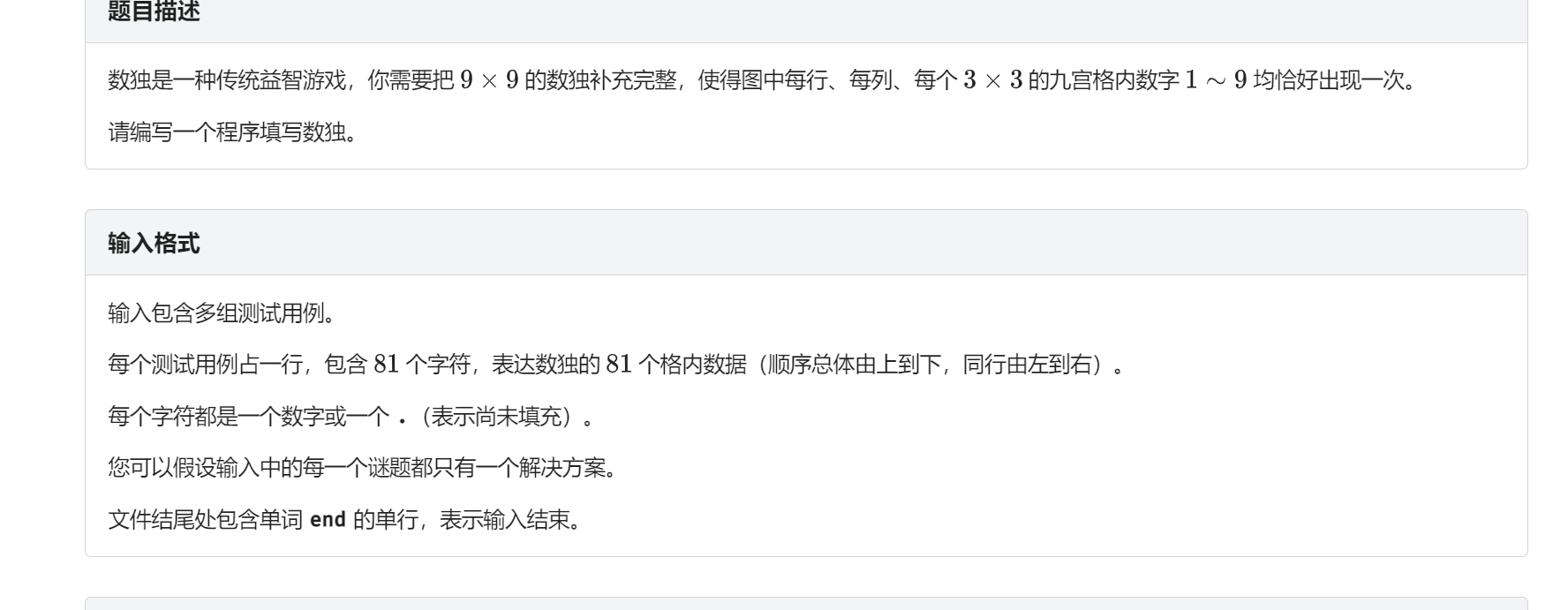
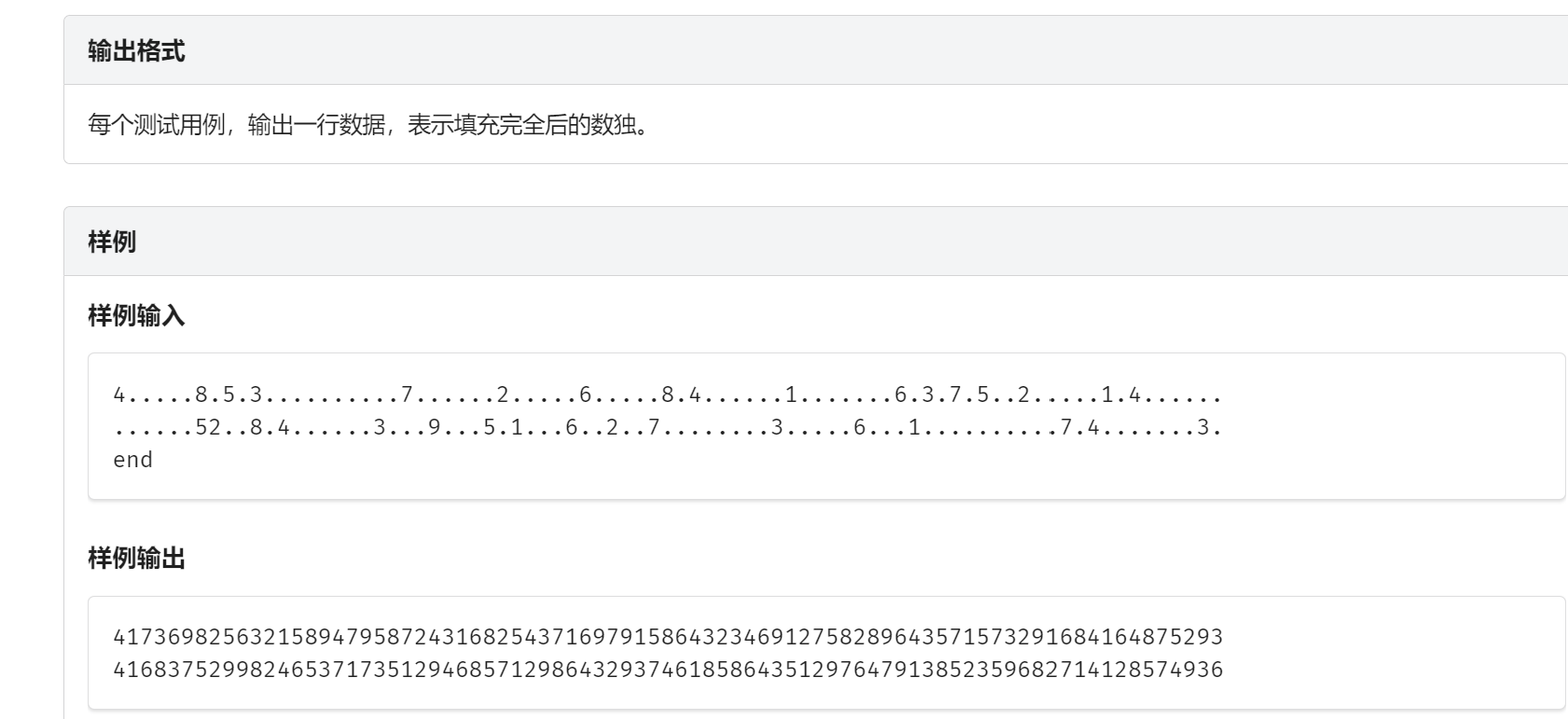
题目分析:
选择一个当前可选的数最小的位置,依次填入各个可能填入的数。
考虑怎么实现:
为了快速地得到每个位置可以选择的位置,可以将当前树所在的行、列、九宫格的填入状态压入一个二进制中储存。
Code
#include<bits/stdc++.h>
using namespace std;
const int INF=1e9+7;
int cnt[10004];//cnt[i]存储每个9位二进制数i能被取几次lowbit,即当前状态i先还有几个1,即当前状态还有几个数可选
int num[10004];//num[i]用二进制表示每一个数,lowbit(i)中i位于第几位,i代表第几个数
//num和cnt的值事先被预处理好,不会在过程中被改变
int tot;//表示开始时未被填入数字的格子数有多少
int mapp[10][10];//存储每个位置所存的数字
int a[10],b[10],c[10];//a,b,c分别存储行、列、九宫格中的每个数是否可选的状态(压成二进制表示)
char s[82];
int f(int x,int y){return x/3*3+y/3;}//f函数可以快速得到每个点所在九宫格的编号
int lowbit[5005];
void change(int x,int y,int v)
{
a[x]^=(1<<v);
b[y]^=(1<<v);
c[f(x,y)]^=(1<<v);
}//把v对应的位数更改一下(这里用xor更改,因此可以完成两种修改:不可选->可选 or 可选->不可选
bool dfs(int idx)
{
if(idx==tot+1) return true;
int Minv=INF,x=0,y=0;
for(int i=0;i<9;++i)
{
for(int j=0;j<9;++j)
{
if(mapp[i][j]!=-1) continue;
int state=a[i]&b[j]&c[f(i,j)];
if(cnt[state]==0) return false;
if(cnt[state]<Minv) Minv=cnt[state],x=i,y=j;
}
}
int state=a[x]&b[y]&c[f(x,y)];
for(;state;state-=lowbit[state])
{
int val=num[lowbit[state]];
mapp[x][y]=val;
change(x,y,val);
if(dfs(idx+1)) return true;
change(x,y,val);
mapp[x][y]=-1;
}
return false;
}
void work()
{
tot=0;
for(int i=0;i<9;++i) a[i]=b[i]=c[i]=(1<<9)-1;
for(int i=0;i<9;++i)
{
for(int j=0;j<9;++j)
{
char ch=s[i*9+j];
if(ch=='.') tot++,mapp[i][j]=-1;
else mapp[i][j]=ch-'1',change(i,j,mapp[i][j]);
}
}
dfs(1);
for(int i=0;i<9;++i)
for(int j=0;j<9;++j)
printf("%d",mapp[i][j]+1);
printf("\n");
}
int main()
{
for(int i=0;i<(1<<9);++i) lowbit[i]=i&(-i);
for(int i=0;i<9;++i) num[1<<i]=i;
for(int i=0;i<(1<<9);++i)
for(int j=i;j;j-=lowbit[j])
cnt[i]++;
while(scanf("%s",s),s[0]!='e') work();
return 0;
}



