YBTOJ内存管理（堆的应用）

题面

题目分析

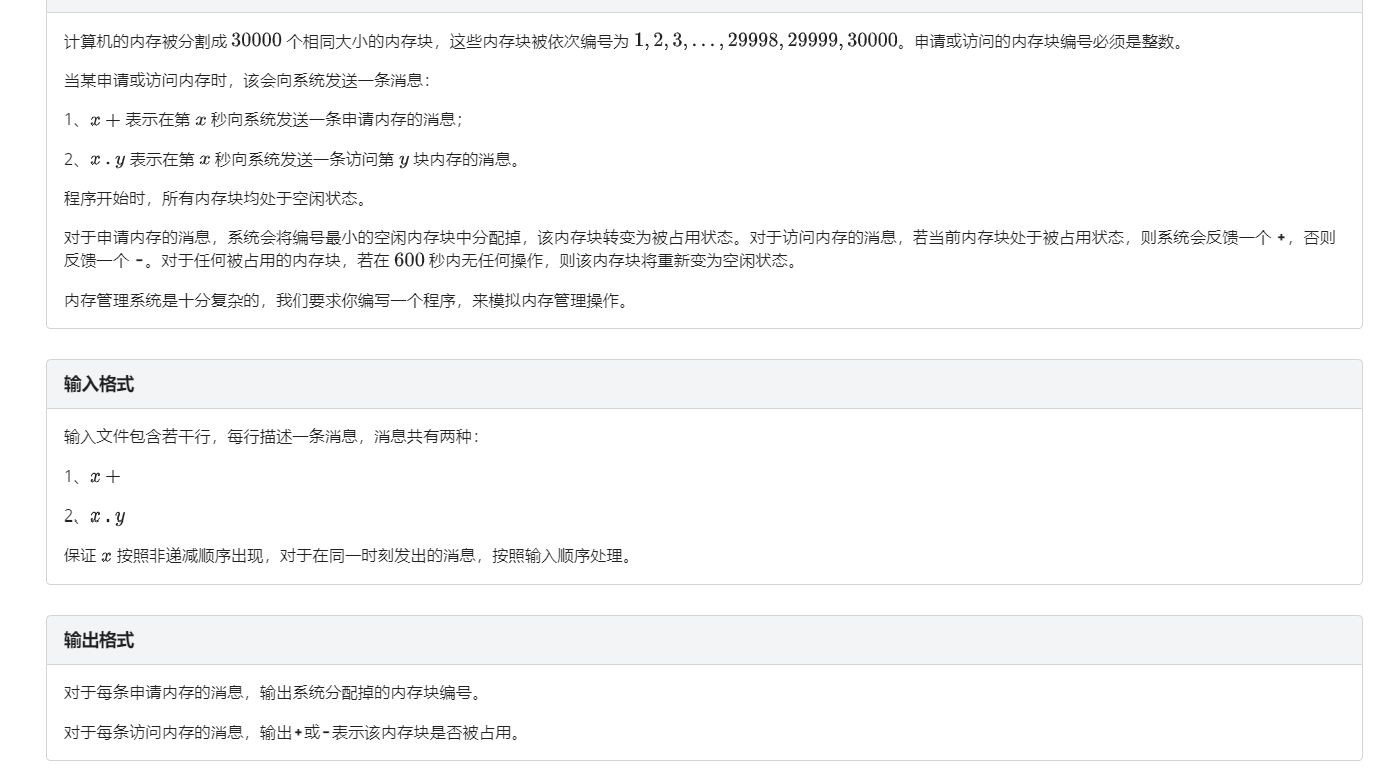
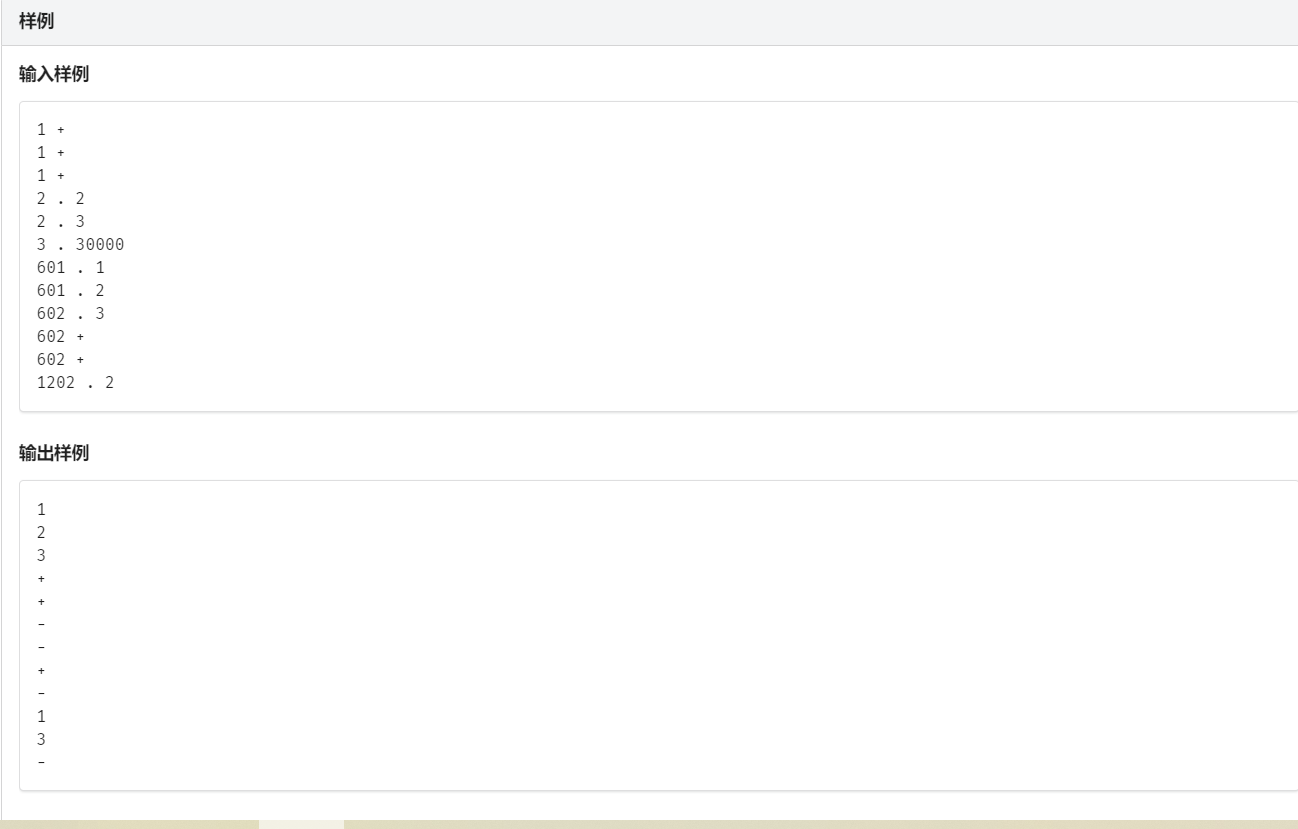
这题最大的特点就是细节很多，注意审题。
(1)如果被占用，则必须过600s(包括当前这一秒)才能恢复空的状态。
而如果这期间内存被查询了，则需要再过600s才能被再次使用。

(2)如果一个内存没有被占用，则查询不会将它变为占用的状态。

(3)发出占用一个内存的请求时，优先占用编号最小的内存点。

算法设计：

写两个小根堆，第一个堆heap1存储未被占用的点的编号，第二堆heap2存储被占用的点开始被占用的时间。

每次输入得到一个当前时间n，则不断地取出heap2的堆顶，若堆顶已经不再被占用，则将其插入heap1中，直到出现一个仍被占用的点，则循环结束。
然后再判断要求的操作，若为请求占用空间，则取出heap1堆顶，插入heap2中，若为判断，则用vis数组处理。

然后就会发现我们忘记了一个问题：
如果一个点在仍被占用时查询器状态，就会把它需要等待的时间恢复到600s,但这个点不一定是heap2堆顶，我们也就无法取出它并且进行修改。

但是不需要取出啊，我们可以再用一个数组change[i]表示一个点在被占用的时候被查询的时间点，每次在取出heap2堆顶的过程中，对每一个取出的点判断其change数组是否合法，若不合法，则令其time=change，完成更新，插回heap2中。

Code

#include<bits/stdc++.h>
using namespace std;
const int maxn=3e4+40;
int len1,len2,heap1[maxn];
int change[maxn];
bool vis[maxn];
struct mint
{
	int id,time;	
}heap2[maxn];
void insert1(int k)
{
	heap1[++len1]=k;
	int pla=len1;
	while(pla>1)
	{
		int fa=pla/2;
		if(heap1[fa]<heap1[pla]) break;
		swap(heap1[fa],heap1[pla]);
		pla=fa; 	
	}
}
int get1()
{
	int res=heap1[1];
	heap1[1]=heap1[len1--];
	int pla=1;
	while(pla*2<=len1)
	{
		int son=pla*2;
		if(son+1<=len1&&heap1[son]>heap1[son+1]) son++;
		if(heap1[pla]<heap1[son]) break;
		swap(heap1[son],heap1[pla]);
		pla=son;
	}
	return res;
}
void insert2(mint k)
{
	heap2[++len2]=k;
	int pla=len2;
	while(pla>1)
	{
		int fa=pla/2;
		if(heap2[fa].time<heap2[pla].time) break;
		swap(heap2[fa],heap2[pla]);
		pla=fa;
	}
}
mint get2()
{
	mint res=heap2[1];
	heap2[1]=heap2[len2--];
	int pla=1;
	while(pla*2<=len2)
	{
		int son=pla*2;
		if(son+1<=len2 && heap2[son].time>heap2[son+1].time) son++;
		if(heap2[pla].time < heap2[son].time) break;
		swap(heap2[pla],heap2[son]);
		pla=son;
	}
	return res;
}
int main()
{
	int n,q;
	char a;
	for(int i=1;i<=30000;++i) insert1(i);
	while(scanf("%d",&n)!=EOF)
	{
		while(1)
		{
			if(len2==0) break; 
			mint g=get2();
			if(g.time+600>n)
			{
				insert2(g);
				break;
			}
			if(change[g.id]+600>n)
			{
				g.time=change[g.id];
				insert2(g);	
			}
			else
			{
				vis[g.id]=false;
				insert1(g.id);		
			}
		}
		cin>>a;
//		printf("%c\n",a);
		if(a!='.')
		{
			int k=get1();
			vis[k]=true;
			mint g;
			g.id=k;
			g.time=n;
			insert2(g);
			printf("%d\n",g.id);
		}
		else
		{
			scanf("%d",&q);	
			if(vis[q]) 
			{
				printf("+\n");
				change[q]=n; 
			}
			else printf("-\n"); 
		}
	}
	return 0;	
}

总结：

根据这个题的分析过程，以及对无法取出的点的更新方式，我们可以得出一些比较普遍性的思路：
(1)多个堆维护多种数据，完成复杂的修改过程。
(2)设置一个额外的数组，来完成对当前无法取出的点的更新，并在它被取出时用这个数组对其判断是否合法，或者更新。