关于树状数组存储&修改&查询前缀和方式的正确性的证明

七月思考过的问题，突然想起来了，就写出来
（才不是因为现在才发现自己写的树状数组里忘记说这个问题了呢！）（大雾）（好怪啊）
（与其说是证明不如说是一个比较严谨且易懂的感性理解）
（大概..还算是严谨吧？）

不会树状数组模板的走传送门：树状数组模板整理

前置设定：a[i]为原数列，c[i]为维护树状数组所用的数组

关于存储方式：

每一个c[i]存储一段从a[i-lowbit（i）+1]到a[i]的长度为lowbit（i)的区间内的数据的和，而lowbit是每一个i在二进制下从最低位起第一个1和这个1之前的所有0组成的数，每一个i都存在lowbit值，因此c[i]存储
a[i-lowbit（i）+1]到a[i]的和,设q=i-bowbit,c[i-lowbit]存储a[q-lowbit(q)+1]到a[i-lowbit]的和......
最终，原序列a[]被所有的c[i]完整的覆盖了，即c数组完整地存储了属于a的所有数据，因此存储是具有正确性的。

关于查询方式：

由于每一个c[i]都存储一段以i为终点，向前延伸至起点i-lowbit(i)+1的长度为lowbit(i)的数组，而c[i-lowbit(i)]也具有相同性质。
从i开始，不断向1延伸，每次加上当前所到达的c[x]的值，则整段从i到1的序列的所有数都被加入了res，因此具有正确性。
（简单来说就是按照模板的方式，i ~ 1的序列会被完整地覆盖，i ~ 1的和也就被不重不漏地求出了）

关于修改方式：

关键在于：a[i]一定被c[i+lowbit(i)]覆盖了。
遇事不决，先分奇偶：
（1）若i为奇数，则根据奇数的性质：奇数在二进制下的第一位一定为1，因此lowbit(i)=1，因此i+lowbit(i)就一定是偶数，偶数在二进制下的第一位一定不为0，因此lowbit(i+1)大于等于2。
就可以发现，i与i+lowbit(i)之间的差为1，而lowbit(i+1)>=2。
即c[i+lowbit(i)]覆盖的区间长度至少为2，一定包含了i。
故得证：i为奇数时，a[i]一定被c[i+lowbit(i)]覆盖

（2）若i为偶数，则取出的lowbit(i)的大小是i的第一个1和该1前面所有的0组成的数的大小，由于进位，i加上lowbit(i)后，生成的新数lowbit(i)+i的第一个1的位置一定比i位于更高位。
即lowbit(lowbit(i)+i)一定大于lowbit(i)。
由于lowbit(i)+i与i之间的差为lowbit(i),而c[lowbit(i)+i]向下覆盖的距离lowbit(lowbit(i)+i)一定大于二者之差lowbit(i)。
同样得证：i为偶数时，a[i]一定被c[i+lowbit(i)]覆盖。

这时候已经得证了，总结一下，可以得出一个容易一些的理解：

无论i的奇偶性，c[lowbit(i)+i]覆盖的区间长度，一定大于lowbit(i)+i与i之间的差lowbit(i)。
因此a[i]一定被c[lowbit(i)+i]覆盖。

因此，想要找到所有被a[i]影响的c[i]只需不断向上累加lowbit(i),正如模板中的做法。

END

或者我们可以草率一些，直接看图也可以得出修改方式的正确性。

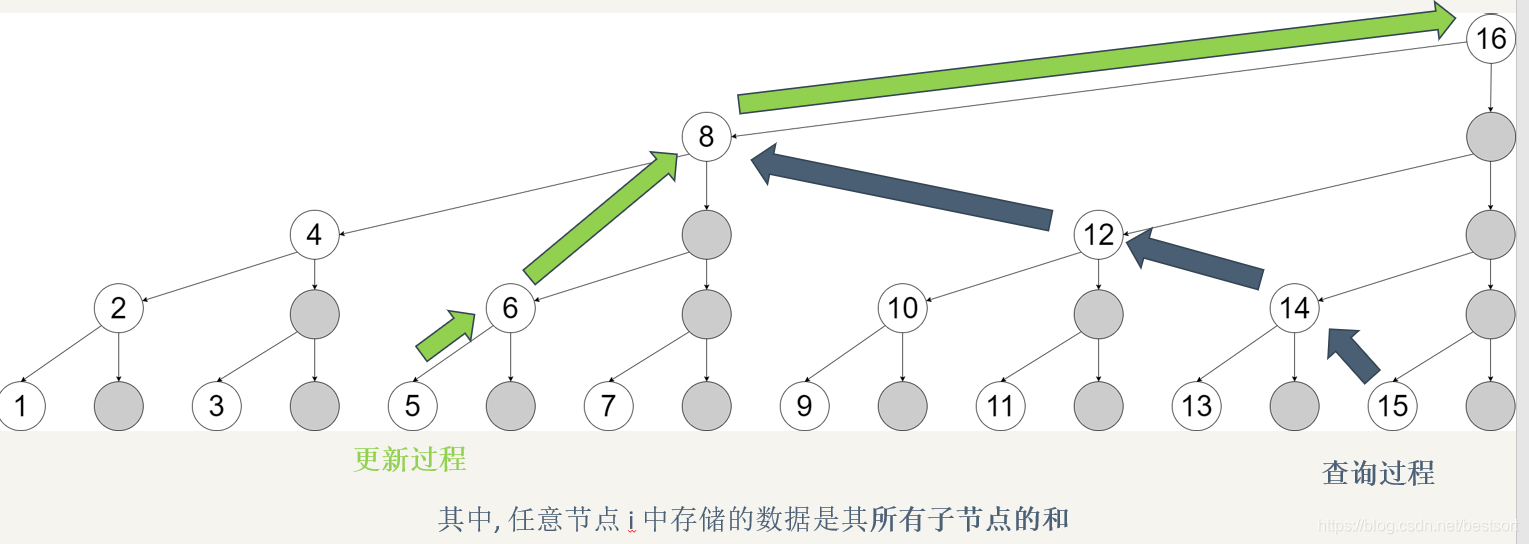
比我那一堆废话好懂多了，不是吗？