codevs 1191 数轴染色 or 染色操作（ybt）

题面

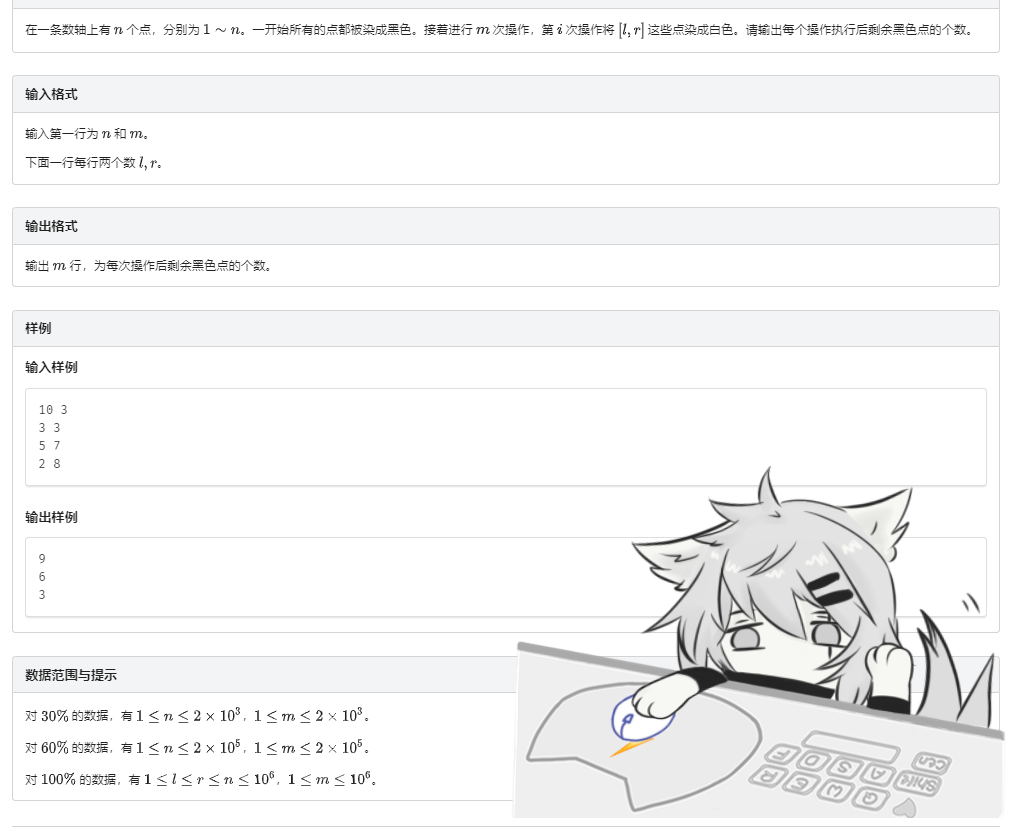
分析：

（1）先考虑暴力：直接每次在数组上暴力修改，复杂度O(n^2)级，估计也就30分
（2）这题属于区间修改和区间查询，可以考虑线段树，初始值全赋成1，修改操作就是将{l,r}之间的数-1，每次查询{1，n}的区间和就是剩余的黑色点数。不过线段树复杂度不够优秀，而且常数巨大，O（nlogn）也就能过
60~70。
(3)树状数组，常数小，但是复杂度和线段树一样，70估计没问题
(4)AC法：用并查集维护的链表加速修改，根据链表的性质，会跳过所有已经被修改过的点，因此每个点最多被处理一次，复杂度O(m+n),
为O（n）极，稳过100

来深入理解一下链表吧

fa[i]表示i右侧（包括i自己）第一个黑色的点的编号
先给出一个初始的数列

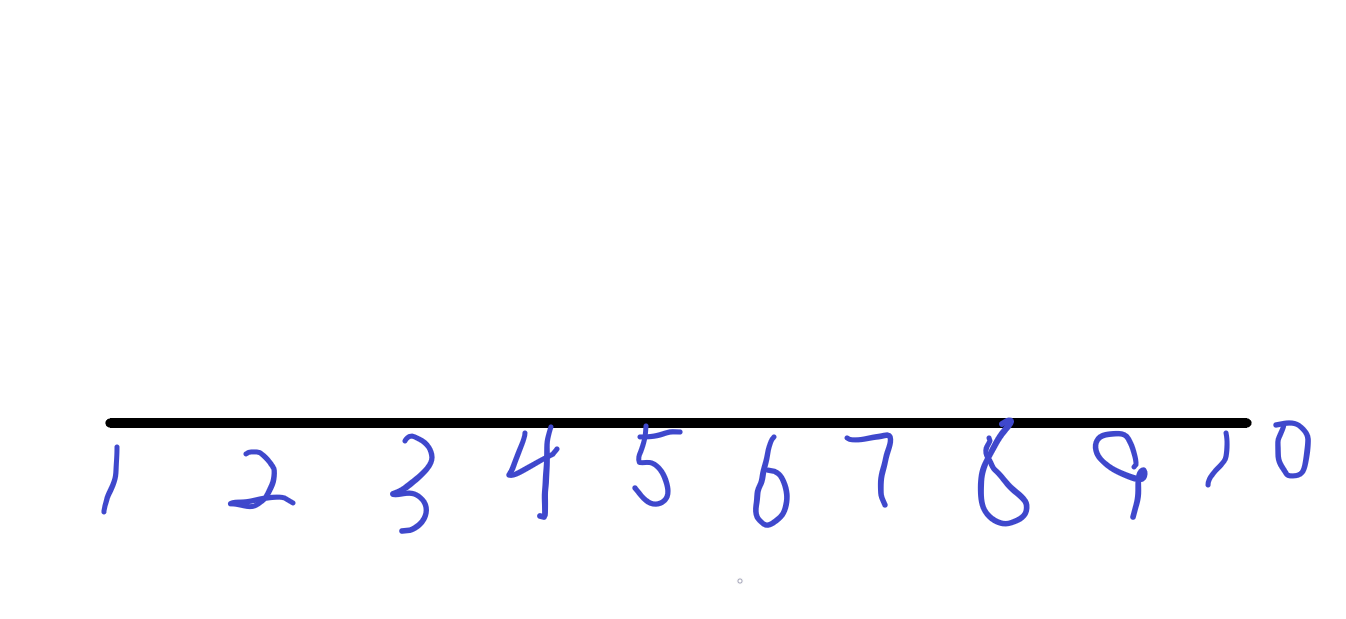
现在我们修改{2,5}

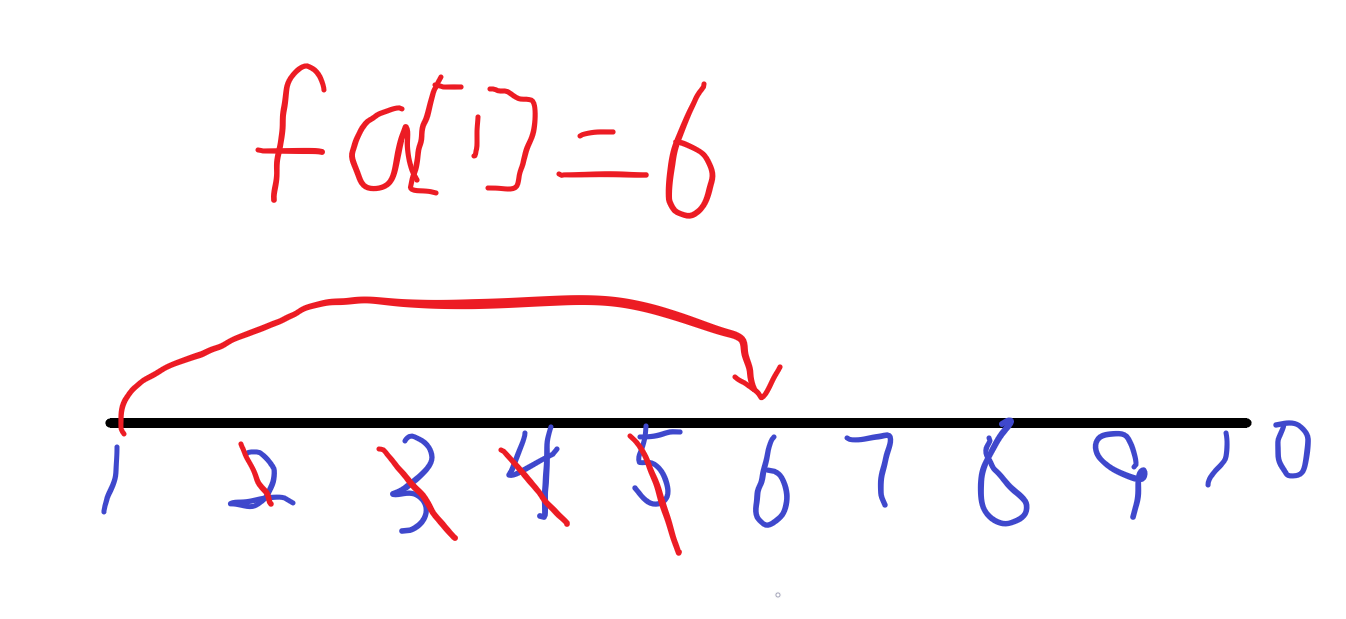
下一次修改的时候，所有已经被修改的点就会被跳过，这就极大地加速了修改的速度，保证每个点最多只会被修改一次，复杂度O(n),非常优秀。

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+40;
int fa[maxn],n,m,l,r; 
int Find(int x)
{ 
	if(fa[x]==x) return x;
	return fa[x]=Find(fa[x]);
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n+1;i++) fa[i]=i; 
	for(int i=1;i<=m;++i)
	{
		scanf("%d%d",&l,&r);
		if(l>r) swap(l,r);
		while(1)
		{
			l=Find(l);
			if(l>r) break;
			else 
			{
				n--;
				fa[l]=l+1;	
			}
		}
		printf("%d\n",n);
	}
	return 0;
}	

对于链表的总结：我们常用链表，跳过已经被修改或去除的部分，以达到优化的效果。

tips：

关于并查集的部分还有一个很恶心的小细节：
每次我们修改链表的过程中，都会这样将l向右传递
看似没什么问题，但是当l==n时，且n为当前要修改的区间的右端点时，
l会继续向右走，直到l>n。
但是，每次我们这样传递l。

fa[l]=l+1

于是乎当ln时，l会继续变成l+1(即n+1),但是按照一般的并查集初始化的习惯，我们只初始化到fa{n},因此fa{n+1}0
此时l+1会进入下面这个语句

l=Find(l);

由于还有下面这个

int Find(int x)
{ 
	if(fa[x]==x) return x;
	return fa[x]=Find(fa[x]);
}

然后l就从n+1跳到了0，而fa{0}还是0，于是就陷入的无限循环中。
结果就爆栈了。

解决方法也不难：

（1）在循环中特判l=0不进入循环

while(1)
		{
			l=Find(l);
			if(l>r || l==0) break;
			else 
			{
				n--;
				fa[l]=l+1;	
			}
		}

（2）初始化到n+1，

fa[n+1]=n+1

(3)不初始化fa，由于fa是全局数组，因此初值为0，可理解成初值为0就是没有被修改
然后写成下面这个样子

int Find(int x)
{ 
	if(fa[x]!=0) return fa[x]=Find(fa[x]);
	//当fa[x]已经被更新时，向右寻找其他黑色的点
	return x;
	//当fa[x]没被更新时，x右侧第一个黑色的点一定是x自己
}

正确性：
Find(n+1)返回n+1,n+1>n因此会跳出循环，避免了死循环的情况。