st表模板--RMQ问题（求区间最大最小值）

算法基础：倍增+dp

算法流程

（1）合并（预处理）：把每一个大的区间分成两部分，求其最大值
（2）查询，求log（len），由一个从区间首端开始和一个由区间尾端开始的长度均为2^log(len)的两个区间中的最大值相互比较，求得最大值。

tips：f[i][j]代表以i为起点，长度为2^j的区间中的最大or最小值

图示

合并（预处理）

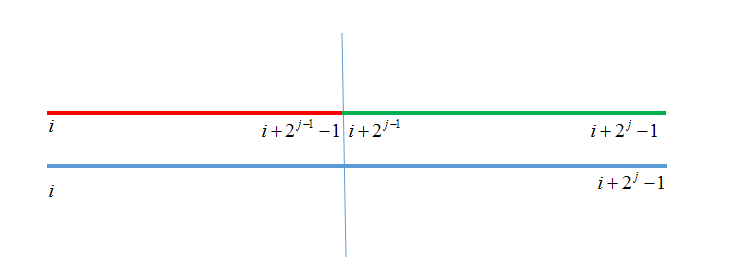
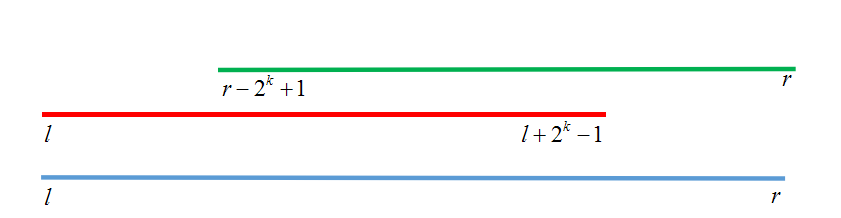
查询

st表的优点

复杂度优秀： 当区间合并复杂度为O(1)时，预处理O（nlogn），查询O（1）

局限性

根据复杂度原理，优秀的复杂度意味着数据信息的部分缺失。
st最大的局限有两点：
（1）不支持修改
（2）如果区间不可重叠（如区间乘），则不可使用st表

Code
ps：给出的模板是求区间最大值，若要求区间最小值，把dp转移式中的max改成min即可（求min不要忘记把输出赋成极大值INF！！！！！）

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
int n,Log[maxn],f[maxn][35],a[maxn],m,x,y;
void init()
{
	scanf("%d%d",&n,&m);	
	for(int i=1;i<=n;++i) scanf("%d",&a[i]);
	Log[0]=-1;
	for(int i=1;i<=n;++i) Log[i]=Log[i>>1]+1;//预处理1~n的log值，因为调用log函数复杂度是O（logn），如果每次查询都调用log函数，那么查询就变成了O（logn）
	for(int i=1;i<=n;++i) f[i][0]=a[i];
	for(int j=1;j<=Log[n];++j)
	{
		for(int i=1;i+(1<<j)-1<=n;++i)
		{
			f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);	
		}
	}	
}//直接用一个函数完成st表预处理
int main()
{
	init();
	int x,y; 
	for(int i=1;i<=m;++i)
	{
		scanf("%d%d",&x,&y);	
		int k=Log[y-x+1];
		int ans=max(f[x][k],f[y-(1<<k)+1][k]);
		printf("%d\n",ans);
	}
	return 0;
}