树状数组整理

树状数组基本性质：
(1)C[i] = A[i - 2^k+1] + A[i - 2^k+2] + ... + A[i]; //k为i的二进制中从最低位到高位连续零的长度
(2)SUMi = C[i] + C[i-2^k1] + C[(i - 2^k1) - 2^k2] + .....；
(3)A[i] 包含于 C[i + 2^k]、C[(i + 2^k) + 2^k]...；

树状数组：a[maxn]是原序列，c[maxn]是树状数组的维护序列（存储一颗树）

基本运用
lowbit

int lowbit(int x)
{
    return x&(-x);
}

无区间修改时
一、单点修改

单点修改
void updata(int i,long long k) //在i位置加上k
{   
    while(i <= n)
	{
        c[i] += k;
        i += lowbit(i);
    }
}

二、区间查询

区间查询
long long getsum(int i)////求A[1 到 i]的和
{        
    long long res = 0;
    while(i > 0)
    {
        res += c[i];
        i -= lowbit(i);
    }
    return res;
}
//l到r的区间和=getsum(r)-getsum(l-1);

三、单点查询：
value[k]=getsum(k)-getsum(k-1)
把一个点当作长度为1的区间即可

有区间修改时：
一、区间修改&单点查询
直接修改每个值一定会复杂度爆炸
很容易想到，要用差分建树：由于在某一区间内加上或减去某一个值，区间内各个值之间的差是不变的。
因此只要修改区间头尾l和r+1两个点的值。
这样写复杂度就ok了。

实现：
规定A[0]=0;
则有 A[i] = ΣD[j](j从1一直增加到i）;(D[j] = A[j] - A[j-1])，即前面i项的差值和。
当某个区间[x,y]值改变了，区间内的差值是不变的，只有D[x]和D[y+1]的值发生改变。
因此只修改x和y+1的正确性是显然的。

代码中选择对数组D建立树状数组

int n,m;
int a[50005] = {0},c[50005]; //对应原数组和树状数组

int lowbit(int x)
{
	return x&(-x);
}
 
void updata(int i,int k)
{    //在i位置加上k
	while(i <= n)
	{
		c[i] += k;
        i += lowbit(i);
    }
} 
int getsum(int i)
{        //求D[1 - i]的和，即A[i]值
	int res = 0;
	while(i > 0)
	{
		res += c[i];
		i -= lowbit(i);
    }     
	return res;
}
int main()
{
	cin>>n;
	for(int i = 1; i <= n; i++)
	{
        cin>>a[i];
        updata(i,a[i] - a[i-1]);   //输入初值的时候，也相当于更新了值
    }
    //[x,y]区间内加上k
    updata(x,k);    //A[x] - A[x-1]增加k
    updata(y+1,-k);        //A[y+1] - A[y]减少k
    //查询i位置的值
    int sum = getsum(i);
    return 0;
}

二、区间查询&&区间修改
既然有区间修改那么就一定要利用差分
已知如下

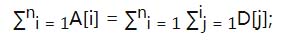
则A[1]+A[2]+...+A[n]

= (D[1]) + (D[1]+D[2]) + ... + (D[1]+D[2]+...+D[n])

= nD[1] + (n-1)D[2] +... +D[n]

= n * (D[1]+D[2]+...+D[n]) - (0D[1]+1D[2]+...+(n-1)*D[n])

因此最开始的公式可变为

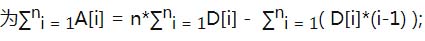
维护两个数状数组，sum1[i] = D[i]，sum2[i] = D[i]*(i-1);

int n,m;
int a[50005] = {0};
int sum1[50005];    //(D[1] + D[2] + ... + D[n])
int sum2[50005];    //(1*D[1] + 2*D[2] + ... + n*D[n])

int lowbit(int x){
    return x&(-x);
}

void updata(int i,int k){
    int x = i;    //因为x不变，所以得先保存i值
    while(i <= n){
        sum1[i] += k;
        sum2[i] += k * (x-1);
        i += lowbit(i);
    }
}

int getsum(int i){        //求前缀和
    int res = 0, x = i;
    while(i > 0){
        res += x * sum1[i] - sum2[i];
        i -= lowbit(i);
    }
    return res;
}

int main(){
    cin>>n;
    for(int i = 1; i <= n; i++){
        cin>>a[i];
        updata(i,a[i] - a[i-1]);   //输入初值的时候，也相当于更新了值
    }

    //[x,y]区间内加上k
    updata(x,k);    //A[x] - A[x-1]增加k
    updata(y+1,-k);        //A[y+1] - A[y]减少k

    //求[x,y]区间和
    int sum = getsum(y) - getsum(x-1);

    return 0;
}