辛普森公式&&自适应辛普森法

一、辛普森公式（二次函数积分公式）：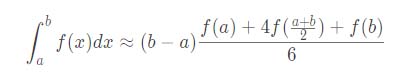
用途：求一个积分的近似值
拓展用途：由于积分的几何意义是函数图像和x轴所围成的图形的面积，因此常用于在计算几何中计算面积
tips1：这里的f(x)可以是任意一个函数。
tips2：但自适应辛普森法只能用于定义域连续不中断的函数（注意是定义域连续不中断即可，函数图像变化不连续不会产生任何影响）。
tips3：求得的结果是近似值而非准确值，因此在某些有精度要求的情况下需要进行分治思想下的精度优化

二、普通辛普森法：、

代码实现：

const int N = 1000 * 1000;
double simpson(double a, double b) 
{
  double h = (b - a) / N;
  double s = f(a) + f(b);
  for (int i = 1; i <= N - 1; ++i) 
  {
    double x = a + h * i;
    s += f(x) * ((i & 1) ? 4 : 2);
  }
  s *= h / 3;
  return s;
}

特点：就是优化了辛普森公式的精度，但是精度仍然略有不足
用途：用途与辛普森公式完全相同

三、自适应辛普森法：
算法的核心思想
由于精度和所用时间互相影响，因此我们需要对于实际问题所需选择适当的计算精度eps，同时保证精度和时间复杂度。

核心思想的转化
精度的核心是分段的方式。因此关键就成为了如何分合适的段数、合适的段的大小。

将问题进一步转化
由于基础的辛普森公式是二次函数积分的近似求法，我们就可以考虑当前要求的f(x)和二次函数的相似程度，以此决定是否要继续分段。
我们这样考虑：假如有一段图像已经很接近二次函数的话，直接带入公式求积分，得到的值精度就很高了，不需要再继续分割这一段了。
于是我们有了这样一种分割方法：每次判断当前段和二次函数的相似程度，如果足够相似的话就直接代入公式计算，否则将当前段分割成左右两段递归求解。

实现思路
现在问题就变成了：如何判断某一段图像和二次函数很接近

我们把当前段直接代入公式求积分，再将当前段从中点分割成两段，把这两段再直接代入公式求积分。如果当前段的积分和分割成两段后的积分之和相差很小的话，就可以认为当前段和二次函数很相似了，不用再递归分割了。

还有一些奇怪的细节
在分治判断的时候，除了判断精度是否正确，一般还要强制执行最少的迭代次数。

const double eps=只要合适设成多少都可以
double simpson(double l, double r)
{
	double mid = (l + r) / 2;
	return (r - l) * (f(l) + 4 * f(mid + f(r)) / 6;  // 辛普森公式
}
double asr(double l, double r, double eqs, double ans, int step) 
{
	double mid = (l + r) / 2;
	double fl = simpson(l, mid), fr = simpson(mid, r);
	if(abs(fl + fr - ans) <= 15 * eqs && step < 0) 
		return fl + fr + (fl + fr - ans) / 15;  // 足够相似的话就直接返回
	return asr(l, mid, eqs / 2, fl, step - 1) + asr(mid, r, eqs / 2, fr, step - 1);  // 否则分割成两段递归求解
}
double calc(double l, double r, double eps)
{
	return asr(l, r, eps, simpson(l, r), 12);
}

代码中“15”这个常数在同等的计算量下可以使结果的精度最优，这一点用数学归纳法挨个尝试各种数据证明即可。

总结
整个过程，是有一个基础的精度不高的公式，一直推出精度和时间复杂度都还算优秀的自适应辛普森法。
而这个算法一般用于计算几何中求图形面积（有一些不会正解的题可以用这个算法水暴力分）。
在二维和三维的计算几何中可以用多次这个算法，来求体积或球体表面积（面积的积分是体积）

例题
洛谷自适应辛普森法模版1