数列找不同 && 小Z的袜子(基础莫队模版)
数列找不同
**莫队的算法思路:
(1)把m个查询排序:左端点为第一关键字,右端点为第二关键字
(2)维护一个序列(pl,pr),每次根据查询区间(l,r)将pr,pl加一或减一进行修改
由于之前已经对查询进行了排序,因此调整的复杂度很低,接近O(N * sqrt(N))
注意:初始状态pl=1,pr=0,表示区间中没有任何一个数
细节问题都在注释里
上代码
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=1e5+5;
int n,m;
int a[N],buc[N],bel[N];//a[i]是输入数据,buc[i]是有多少对i(桶)
//bel[i]是第i个数所属的块的编号,则有bel[i]=i/B+1(B是块的长度)
int len;
long long qans;//qans是答案(有多少对相同的数)
/*
关于pans值的意义:在所维护的区间内有pans对相同的数
关于pans值的可能情况:
(1)pans=0 没有相同的数
(2)pans>0 有pans对相同的数
(3)pans<0 ...根据实际意义不可能存在这种情况
*/
int pl=1,pr=0;
inline void add(int k)
{
qans+=buc[a[k]]++;
}//将第k个点加入维护的区间:由于a[k]和序列中原有的buc[a[k]]个a[k]成了buc[a[k]]对相同的数,故写成如上的形式
//注意!!!:这一句的意义是先算qans+=buc[a[k]],再算buc[a[k]]++;
inline void del(int k)
{
qans-=--buc[a[k]];
}//将第k个点从维护的区间中去掉:由于a[k]和序列中原有的buc[a[k]]-1个a[k]成了buc[a[k]]-1对相同的数,因此写法如上
//这一句的意义是先算buc[a[k]]-1.再算qans-=buc[a[k]]
inline int calc(int l,int r)//l,r是目标区间
{
while(pl>l)add(--pl);//当pl>l,将pl向左移,将a[pl-1]对答案pans的贡献加入pans
while(pr<r)add(++pr);//当pr<r,将pr向右移,将a[pr+1]对答案pans的贡献加入pans
while(pl<l)del(pl++);//当pl<l,将pl向右移,将a[pl]对答案pans的贡献从pans中去掉
while(pr>r)del(pr--);//当pr>r.将pr向左移,将a[pr]对答案pans的贡献从pans中去掉
return qans;//返回当前的答案
}
struct ask
{
int l,r,id;
}q[N];//存储每次询问的左右端点以及序号
bool cmp(ask a,ask b)
{
return bel[a.l]!=bel[b.l] ? a.l<b.l : a.r<b.r;
}//把询问按左端点为第一关键字,右端点为第二关键字排序
bool ans[N];
int main()
{
scanf("%d%d",&n,&m);
len=ceil(sqrt(n));//向下取整,得到每一个分块的长度
for(int i=1;i<=n;++i)
{
scanf("%d",&a[i]);
bel[i]=i/len+1;
}//分块操作:算出第i个数所在的块的编号bel[i]
for(int i=1;i<=m;++i)
{
scanf("%d%d",&q[i].l,&q[i].r);
q[i].id=i;
}
sort(q+1,q+m+1,cmp);
for(int i=1;i<=m;++i)
{
int l=q[i].l;
int r=q[i].r;
int id=q[i].id;
ans[id]=!calc(l,r);
}
for(int i=1;i<=m;++i) printf("%s\n",ans[i]?"Yes":"No");
return 0;
}
P1494 [国家集训队]小Z的袜子
和上一道题没什么区别
细节:
(1)最简分数:求分子分母的gcd(最大公因数),并将分子分母分别除以gcd
(2)可能性计算:ans = calc(l,r) / (r-l+1)*(r-l)/2;
code
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int maxn=5e4+5;
int n, m, qans=0,pl=1,pr=0,bel[maxn],a[maxn],len,buc[maxn], sto, ans[maxn][3];
struct ask
{
int l,r,id;
}q[maxn];
bool cmp(ask a,ask b)
{
return bel[a.l]!=bel[b.l] ? a.l<b.l : a.r<b.r;
}
inline void add(int k)
{
qans+=buc[a[k]]++;
}
inline void del(int k)
{
qans-=--buc[a[k]];
}
/*
int gcd(long long x,long long y) return y ? gcd(y,x%y) : x;//不使用c++11的把这一行加上
*/
inline int calc(int l,int r)
{
while(pl>l) add(--pl);
while(pr<r) add(++pr);
while(pl<l) del(pl++);
while(pr>r) del(pr--);
return qans;
}
int main()
{
scanf("%d%d",&n,&m);
len=ceil(sqrt(n));
for(int i=1;i<=n;++i)
{
scanf("%d",&a[i]);
bel[i]=i/len+1;
}
for(int i=1;i<=m;++i)
{
scanf("%d%d",&q[i].l,&q[i].r);
q[i].id=i;
}
sort(q+1,q+m+1,cmp);
for(int i=1;i<=m;++i)
{
int l=q[i].l, r=q[i].r, id=q[i].id;
if(l==r)
{
ans[id][0]=0;
ans[id][1]=1;
continue;
}
ans[id][0]=calc(l,r);
ans[id][1]=1ll*(r-l+1)*(r-l)/2;
long long k=__gcd(ans[id][0],ans[id][1]);
ans[id][0] /= k;
ans[id][1] /= k;
}
for(int i=1;i<=m;++i) printf("%d/%d\n", ans[i][0],ans[i][1]);
return 0;
}
莫队的优化:奇偶优化
最好根据图像理解原理
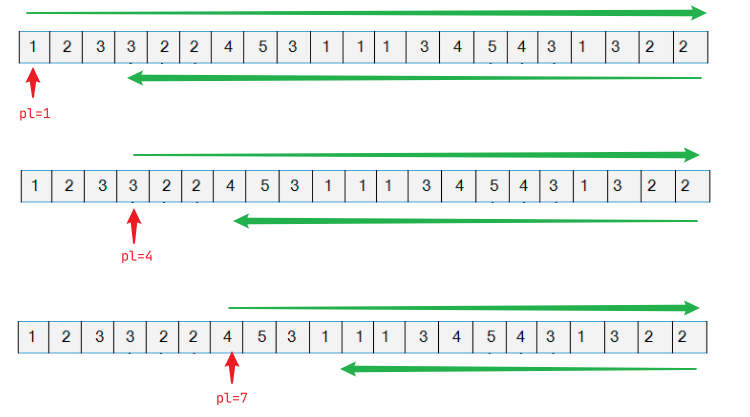
可以发现,对于左端点进入新的一个区间时,右端点需要从N处回到最左边,再跑回到最右边。这样也是进行了很多次多余的扩展。
提供一种奇偶优化的方案:
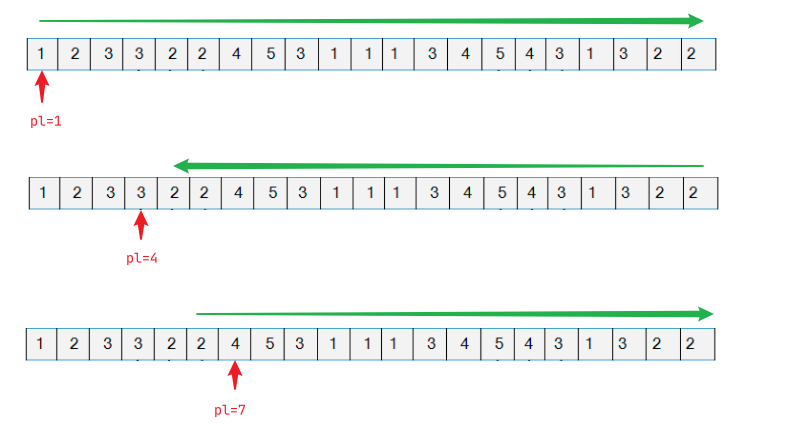
对于分块标号为奇数的,按p[i].r升序排列,反之偶数按p[i].r降序排列。效果如下:
代码实现:
只需将排序一处的代码修改:
如果a.l与b.l在同一个块内,则:
如果所在块编号是奇数,则按a.l<b.l排列;
如果所在块编号是偶数,则按a.l>b.l排列。
如果不在同一个块内,则左端点编号小的在前。
所以代码为:
bool cmp(ask a,ask b)
{
return bel[a.l] == bel[b.l] ? (bel[a.l] & 1 ? a.r < b.r : a.r > b.r): a.l < b.l;;
}
PS:关于奇偶优化
这个优化并没能减小算法的复杂度,实质常数级的优化,是通过减小不必要的操作来使实际复杂度更接近莫队的理想复杂度O(N*sqrt(N))。
But:奇偶优化目前看来只会让代码更快,一定不会使复杂度更差。
更何况莫队作为一个重要算法,很可能被卡常,因此,在保证正确性的情况下,能写一定要写!!!
万一25个点有20个卡莫队呢?总之写了才会有可能rp++。不写只会被卡。
带修莫队
方案是增加一个时间轴T.
可以增加一个变量now,表示当前处理的询问之前执行过多少次修改。
对于每一次查询,记录当前查询之前进行多少修改
#include <bits/stdc++.h>
#define fo(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout)
using namespace std;
const int INF = 0x3f3f3f3f , N = 1.4e5+5 , M = 1e6+5;
typedef long long ll;
typedef unsigned long long ull;
inline ll read(){
ll ret = 0 ; char ch = ' ' , c = getchar();
while(!(c >= '0' && c <= '9')) ch = c , c = getchar();
while(c >= '0' && c <= '9')ret = (ret << 1) + (ret << 3) + c - '0' , c = getchar();
return ch == '-' ? - ret : ret;
}
int n,m;
int a[N];
int pl=1,pr,pans,len,bel[N];
int buc[M],now;
int ans[N];
struct ask{int l,r,id,t;}q[N];int qcnt;
inline bool operator < (const ask a,const ask b){return bel[a.l] == bel[b.l] ? bel[a.r] == bel[b.r] ? a.t<b.t : a.r<b.r : a.l < b.l;}
struct mdf{int p,v;}mo[N];int mcnt;
inline void mod(int k,int id){
if(q[id].l <= mo[k].p && mo[k].p <= q[id].r)
pans += !buc[mo[k].v]++,
pans -= !--buc[a[mo[k].p]];
swap(mo[k].v,a[mo[k].p]);
}
inline void add(int k){pans += !buc[a[k]]++;}
inline void del(int k){pans -= !--buc[a[k]];}
inline int calc(int l,int r,int id,int t){
while(pl > l)add(--pl);
while(pr < r)add(++pr);
while(pl < l)del(pl++);
while(pr > r)del(pr--);
while(now < t)mod(++now,id);
while(now > t)mod(now--,id);
return pans;
}
signed main(){
n = read() , m = read();
len = pow(n,2.0/3);
for(int i = 1 ; i <= n ; i ++)
a[i] = read(),
bel[i] = i / len + 1;
for(int i = 1 ; i <= m ; i ++){
char ch[2];int x,y;
scanf(" %s %d %d",ch,&x,&y);
if(ch[0] == 'Q')q[++qcnt] = (ask){x,y,qcnt,mcnt};
else mo[++mcnt] = (mdf){x,y};
}
sort(q+1,q+qcnt+1);
for(int i = 1 ; i <= qcnt ; i ++)
ans[q[i].id] = calc(q[i].l,q[i].r,i,q[i].t);
for(int i = 1 ; i <= qcnt ; i ++)
printf("%d\n",ans[i]);
return 0;
}


