[CV] 小波变换
小波变换
函数空间\(f(x)\in V\)
\[V=\overline{S P A N \varphi_{k}(x)}
\]
所有构成函数空间\(V\)的基函数都是归一化正交的(orthonormal basis),即任意两个基函数之间都是归一化正交的(orthonormal)
正交:https://zh.wikipedia.org/wiki/正交
尺度函数
母函数
\[\varphi_{j, k}(x)=2^{j / 2} \varphi\left(2^{j} x-k\right)
\]
- k是平移,沿着x轴的位置
- j是尺度,沿着x轴的宽度
每个尺度j都有对应的子空间
\[V_{j}=\overline{S P A N \varphi_{j, k}(x)} \quad \text { if } f(x) \in V_{j}, \quad f(x)=\sum_{k} \alpha_{k} \varphi_{j, k}(x)
\]
同时:
\[\varphi_{j, k}(x)=\sum_{n} \alpha_{n} \varphi_{j+1, n}(x)
\]
而小波函数(wavelet function):
相邻两个尺度之间的\(V_j\)和\(V_{j+1}\)的差异区域
\[\psi_{j, k}(x)=2^{j / 2} \psi\left(2^{j} x-k\right)
\]
函数空间可以通过至少一个尺度函数和小波函数来表达
\[L^{2}(\mathbf{R})=V_{j_{0}} \oplus W_{j_{0}} \oplus W_{j_{0}+1} \oplus \cdots
\]
小波函数系数:
\[\psi(x)=\sum_{n} h_{\psi}(n) \sqrt{2} \varphi(2 x-n)
\]
哈尔(Haar)小波
尺度函数:
\[\varphi(x)=\left\{\begin{array}{ll}
1 & 0 \leq x<1 \\
0 & \text { otherwise }
\end{array}\right.
\]
小波函数:
\[\psi(x)=\left\{\begin{array}{ll}
1 & 0 \leq x<0.5 \\
-1 & 0.5 \leq x<1 \\
0 & \text { elsewhere }
\end{array}\right.
\]
哈尔小波生成函数:
\[\psi_{j, k}(x)=2^{j / 2} \psi\left(2^{j} x-k\right)
\]
函数\(f(x)\)的小波序列展开(wavelet series expansion)
\[f(x)=\sum_{k} c_{j_{0}}(k) \varphi_{j_{0}, k}(x)+\sum_{j=j_{0}}^{\infty} \sum_{k} d_{j}(k) \psi_{j, k}(x)
\]
例子:
\[f(x)=\left\{\begin{array}{ll}
x^{2} & 0 \leq x<1 \\
0 & \text { otherwise }
\end{array}\right.
\]
计算系数:计算\(f(x)\)在\([0,1)\)区间的初始尺度系数和二次方展开每层的小波系数
哈尔小波序列展开估计原函数:
\[f(x)=\frac{1}{3} \varphi_{0,0}(x)+\left[-\frac{1}{4} \psi_{0.0}(x)\right]+\left[-\frac{\sqrt{2}}{32} \psi_{1,0}(x)-\frac{3 \sqrt{2}}{32} \psi_{1,1}(x)\right]+\ldots
\]
小波变换(discrete wavelet transform)
正变换
\[W_{\varphi}\left(j_{0}, k\right)=\frac{1}{\sqrt{M}} \sum_{x} f(x) \varphi_{j_{0}, k}(x)
\]
\[W_{\psi}(j, k)=\frac{1}{\sqrt{M}} \sum_{x} f(x) \psi_{j, k}(x), \quad j \geq j_{0}
\]
\(j_0=0\),\(j\)的取值范围\([0,J-1]\),\(k\)的取值范围\([0,2^{j}-1]\),\(x\)的取值范围\([0,M-1]\)
反变换
\[f(x)=\frac{1}{\sqrt{M}} \sum_{k} W_{\varphi}\left(j_{0}, k\right) \varphi_{j_{0}, k}(x)+\frac{1}{\sqrt{M}} \sum_{j=j_{0}}^{\infty} \sum_{k} W_{\psi}(j, k) \psi_{j, k}(x)
\]
快速小波变换(后续补充)
二维小波变换
\[\begin{array}{l}
\varphi(x, y)=\varphi(x) \varphi(y) \\
\psi^{H}(x, y)=\psi(x) \varphi(y) \\
\psi^{V}(x, y)=\varphi(x) \psi(y) \\
\psi^{D}(x, y)=\psi(x) \psi(y)
\end{array}
\]
\[\begin{aligned}
\varphi_{j, m, n}(x, y) &=2^{j / 2} \varphi\left(2^{j} x-m, 2^{j} y-n\right) \\
\psi_{j, m, n}^{i}(x, y) &=2^{j / 2} \psi^{i}\left(2^{j} x-m, 2^{j} y-n\right), \quad i=\{H, V, D\}
\end{aligned}
\]
\[\begin{aligned}
W_{\varphi}\left(j_{0}, m, n\right) &=\frac{1}{\sqrt{M N}} \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) \varphi_{j_{0}, m, n}(x, y) \\
W_{\psi}^{i}(j, m, n) &=\frac{1}{\sqrt{M N}} \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) \psi_{j, m, n}^{i}(x, y)
\end{aligned}
\]
小波变换可分离,因此可以先进行行变换后对结果再进行列变换
实践
Python对应的库https://pywavelets.readthedocs.io/en/latest/
二维离散对应函数小波变换正变换dwt2,小波逆变换idwt2
原图:

img = cv2.imread(path.join(resource_path,"fzuimage2.jpg"),cv2.IMREAD_GRAYSCALE)
# import pywt.data
# img = pywt.data.camera()
img = img[:256,:256]
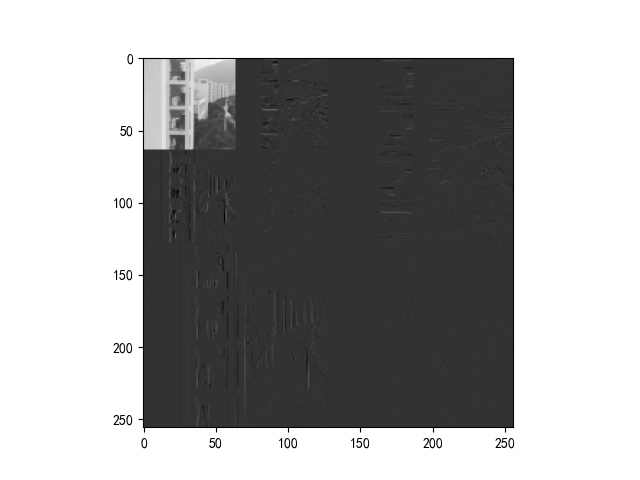
C0,C1,C2 = pywt.wavedec2(img,'haar',level=2)
trans = np.vstack((np.hstack((np.vstack((np.hstack((C0,C1[0])),np.hstack(tuple(C1[1:])))),C2[0])),np.hstack(tuple(C2[1:]))))
plt.figure(1)
plt.imshow(trans,cmap="gray")
plt.figure(2)
plt.imshow(pywt.waverec2((C0,C1,C2),'haar'),cmap="gray")
plt.show()