算法第三章作业

1、编辑距离问题

题目：设A和B是2个字符串。要用最少的字符操作将字符串A转换为字符串B。这里所说的字符操作包括：(1)删除一个字符；(2)插入一个字符；(3)将一个字符改为另一个字符。将字符串A变换为字符串B所用的最少字符操作数称为字符串A到B的编辑距离，记为d(A,B)。对于给定的字符串A和字符串B，计算其编辑距离 d(A,B)。

输入格式:

第一行是字符串A，文件的第二行是字符串B。

提示：字符串长度不超过2000个字符。

输出格式:

输出编辑距离d(A,B)

输入样例:

fxpimu
xwrs 

输出样例:

5

1.1 根据最优子结构性质，列出递归方程式

设D[i，j]表示从a[1：i]变为b[1：j]的编辑距离。

对于末尾元素：

1）当做删除操作的时候，只需要删除a[i]，所以D[i，j] = D[i-1，j]+1;

2）当做插入操作的时候，可以看作删除了b[j]，所以D[i，j] = D[i，j-1]+1;

3）当做替换操作的时候，此时a[i]和b[j]不相等，所以D[i，j] = D[i-1，j-1]+1;

4）当不需要进行操作的时候，意味着a[i]和b[j]相等，所以D[i，j] = D[i-1，j-1];

所以 D[i,j] = min{ D[i-1，j]+1, D[i，j-1]+1, D[i-1，j-1]+(a[i]==b[j] ? 0 : 1) }；

再考虑边界情况：

当a为空时，显然，D[i,j] = j;

当b为空时，显然，D[i,j] = i;

所以递归方程式为：

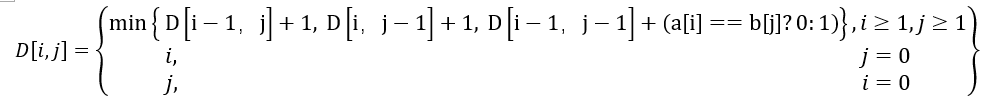
1.2 给出填表法中表的维度、填表范围和填表顺序。

表的维度：2维

填表范围：整张表都要填

填表顺序：先填i=0的情况和j=0的情况，再从上往下，从左往右填。

1.3 分析该算法的时间和空间复杂度

时间复杂度：O(m*n)

空间复杂度：O(m*n)

2、对动态规划算法的理解

按照定义，动态规划是把一个大问题拆解成一堆小问题，但是这些小问题不是相互独立的，他们之间是有联系的，所以我们为了避免重复计算那些小问题，就可以把计算过了的小问题记录下来。所以我对动态规划算法的理解就是构造最优解，创建递归方程，然后利用填表法填表。

3、说明结对编程情况

结对编程情况挺好的，我们的水平差不多，虽然两个人有时候会有不一样的想法，但是经过讨论之后最终还是会达成共识。