Python多重继承排序原理

　　参考：https://www.jianshu.com/p/c9a0b055947b

　　一，什么是拓扑排序

　　在图论中，拓扑排序(Topological Sorting) 是一个 有向无环图(DAG,Directed Acyclic Graph) 的所有顶点的线性序列。且该序列必须满足下面两个条件

　　1，每个顶点出现且只出现一次。

　　2，若存在一条从顶点A到顶点B的路径，那么序列中点A出现在顶点B的前面。

　　例如，下面这个图

 

 

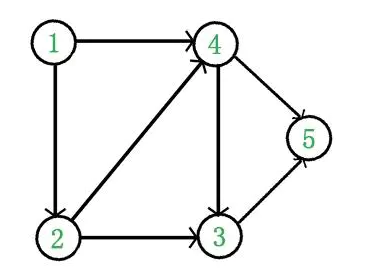
 　　它是一个DAG图，那么如何写出它的拓扑顺序呢？这里说一种比较常用的方法：

　　

• 从DAG途中选择一个没有前驱(即入度为0)的顶点并输出
• 从图中删除该顶点和所有以它为起点的有向边。

• 重复1和2直到当前DAG图为空或当前途中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。

 

 

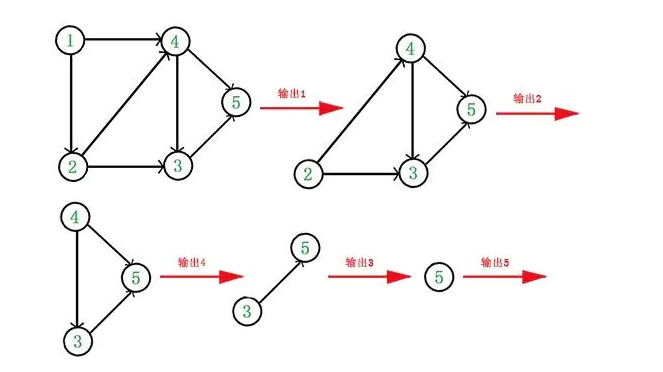
 　　于是，得到拓扑排序后的结果是{1,2,4,3,5}

　　二，Python多重继承

　　多重继承示例

class A(object):
    def foo(self):
        print('A foo')
    def bar(self):
        print('A bar')

class B(object):
    def foo(self):
        print('B foo')
    def bar(self):
        print('B bar')

class C1(A,B):
    pass

class C2(A,B):
    def bar(self):
        print('C2-bar')

class D(C1,C2):
    pass

if __name__ == '__main__':
    print(D.__mro__)
    d=D()
    d.foo()
    d.bar()

　　__mro__属性即为拓扑排序

　　首先，我们根据上面的继承关系构成一张图，如下

　　注意：同级类，按照顺序先定义的类在左边，后定义类在右边

 

 

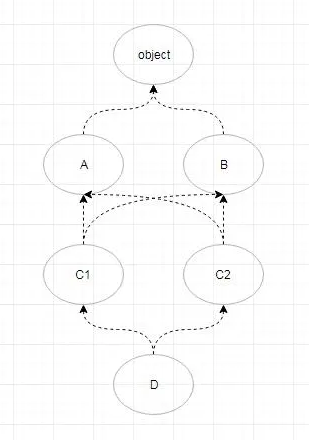
 　　拓扑排序步骤如下

1. 　　找到入度为0的点，只有一个D，把D拿出来，把D相关的边减掉，减掉以后拓扑图如下

   

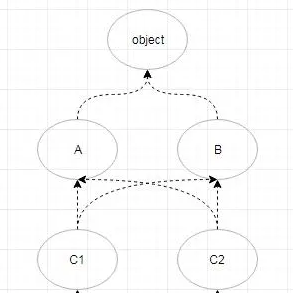
2. 现在有两个入度为0的点(C1,C1),取最左原则，拿C1，减掉C1相关的边，这时候的排序是{D,C1}

　　

 

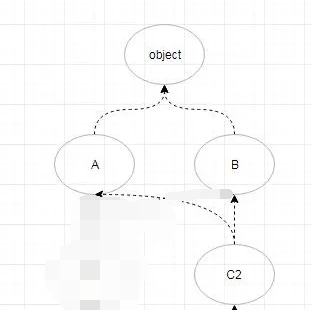
 　　3,现在我们看，入度为0的点(C2),减掉C2相关的边，这时候的排序是{D,C1,C2}

　　

 

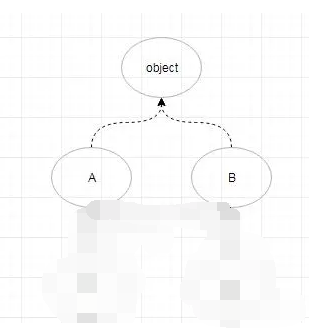
　　4,接着看，入度为0的点（A,B），取最左原则，拿A，剪掉A相关的边，这时候的排序是{D,C1,C2,A}

　　　

 

 　　5,继续，入度为0的点只有B，剪掉B相关的边，最后只剩下object

　　6，所以最后的排序是{D,C1,C2,A,B,object}

　　　我们执行上面的代码，发现print(D.__mro__的结果)，而这也就是多重继承所使用的C3算法啦

(<class '__main__.D'>, <class '__main__.C1'>, <class '__main__.C2'>, <class '__main__.A'>, <class '__main__.B'>, <class 'object'>)

　　再来分析d.foo()和d.bar()会怎么执行，首先D类没有foo方法则继续往上找B和A都有foo方法，但是A顺序在前使用执行A的foo方法，打印如下

A foo

　　同理按照顺序最先找到的是C2的bar方法，打印如下

C2-bar

　　

　　分析下列多重继承的拓扑顺序

class A(object):
    def foo(self):
        print('A foo')
    def bar(self):
        print('A bar')

class B(object):
    def foo(self):
        print('B foo')
    def bar(self):
        print('B bar')

class C1(A):
    pass

class C2(B):
    def bar(self):
        print('C2-bar')

class D(C1,C2):
    pass

if __name__ == '__main__':
    print(D.__mro__)
    d=D()
    d.foo()
    d.bar()

　　图示如下

 

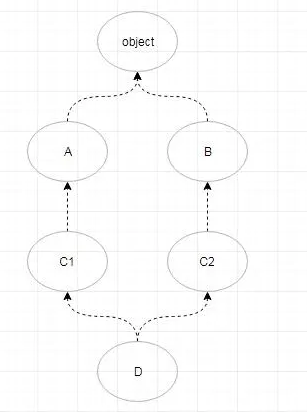
 　　拓扑顺序为{D,C1,A,C2,B,object}