拓扑排序

在一个表示工程的有向图中，用顶点表示活动，用弧表示活动之间的优先关系，这样的有向图为顶点表示活动的网，我们称为AOV网。AOV网中的弧表示活动之间存在的某种制约关系，且不能存在回路。 设G=(V，E)是一个具有n个顶点的有向图， V中的顶点序列v1，v2，……， vn, 满足若从顶点vi到vj有一条路径，则在顶点序列中顶点vi必在顶点vj之前。 则称这样的顶点序列为一个拓扑序列。所谓拓扑排序，其实就是对一个有向图构造拓扑序列的过程。构造时会有两个结果，如果此网的全部顶点都被输出，则说明它是不存在环(回路)的AOV网；如果输出顶点数少了，哪怕是少了一个，也说明这个网存在环(回路)，不是AOV网。
拓扑排序的基本思路是: 从AOV网中选择一个入度为0 的顶点输出，然后删去此顶点，并删除以此顶点为尾的弧，继续重复此步骤，直到输出全部顶点或者AOV网中不存在入度为0的顶点为止。整个算法的时间复杂度为O(n+e)。

拓扑排序的实现步骤:

1.在有向图中选一个没有前驱的顶点并且输出
2.从图中删除该顶点和所有以它为尾的弧（白话就是：删除所有和它有关的边）
3.重复上述两步，直至所有顶点输出，或者当前图中不存在无前驱的顶点为止，后者代表我们的有向图是有环的，因此，也可以通过拓扑排序来判断一个图是否有环。

拓扑排序示例手动实现:

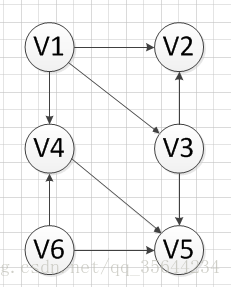
如果我们有如下的一个有向无环图，我们需要对这个图的顶点进行拓扑排序，过程如下：

首先，我们发现V6和v1是没有前驱的，所以我们就随机选去一个输出，我们先输出V6，删除和V6有关的边，得到如下图结果：

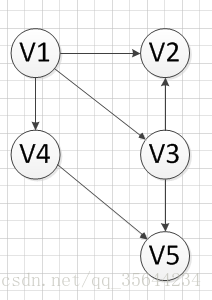
然后，我们继续寻找没有前驱的顶点，发现V1没有前驱，所以输出V1，删除和V1有关的边，得到下图的结果：

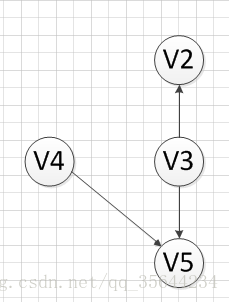
然后，我们又发现V4和V3都是没有前驱的，那么我们就随机选取一个顶点输出（具体看你实现的算法和图存储结构），我们输出V4，得到如下图结果：

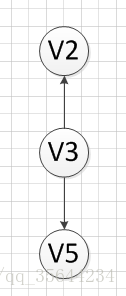
然后，我们输出没有前驱的顶点V3，得到如下结果：

然后，我们分别输出V5和V2，最后全部顶点输出完成，该图的一个拓扑序列为：

v6–>v1—->v4—>v3—>v5—>v2

python代码实现：

class Stack():
    """栈类"""

    def __init__(self):
        self.stack = []

    def Enstack(self, data):
        """入栈操作"""
        self.stack.append(data)

    def Destack(self):
        """出栈操作"""
        return self.stack.pop()

    def isEmpty(self):
        """判断栈是否为空"""
        return not len(self.stack)


class Vertex(object):
    """创建Vertex类，用来存放顶点信息（包括data和firstEdge）"""

    def __init__(self, data=None):
        self.inDegree = 0
        self.data = data
        self.firstEdge = None


class EdgeNode(object):
    """ 创建Edge类，用来存放边信息（包括adjVex和next）；"""

    def __init__(self, adjVex):
        self.adjVex = adjVex
        self.next = None


class ALGraph():
    """有向图类"""

    def __init__(self):
        self.numNodes = 0
        self.numEdges = 0
        self.adjList = []

    def createALGraph(self):
        """如果是无向图，最后三行不能注释掉"""
        self.numNodes = int(input("输入顶点数："))
        self.numEdges = int(input("输入边数："))
        for i in range(self.numNodes):  # 读入顶点信息，建立顶点表
            v = Vertex()
            self.adjList.append(v)
            self.adjList[i].data = input("请输入顶点数据：")
            self.adjList[i].inDgree = int(input("请输入此顶点的入度："))

        for k in range(self.numEdges):  # 建立边表
            i = int(input("请输入边(vi,vj)上的下标i:"))
            j = int(input("请输入边(vi,vj)上的下标j:"))
            e = EdgeNode(j)  # 实例化边节点
            e.next = self.adjList[i].firstEdge  # 将e的指针指向当前顶点指向的节点
            self.adjList[i].firstEdge = e  # 将当前顶点的指针指向e
            # e = EdgeNode(i)  # 实例化边节点
            # e.next = self.adjList[j].firstEdge  # 将e的指针指向当前顶点指向的节点
            # self.adjList[j].firstEdge = e  # 将当前顶点的指针指向e


def TopologicalSort(ALG):
    count = 0  # 用于统计输出顶点的个数
    stack = Stack()  # 建栈将入度为0的顶点入栈
    for i in range(ALG.numNodes):
        if ALG.adjList[i].inDgree == 0:
            stack.Enstack(i)  # 将入度为0的顶点入栈
    while not stack.isEmpty():  # 若栈不为空
        gettop = stack.Destack()  # 出栈
        print("{} ->".format(ALG.adjList[gettop].data), end="")  # 打印此点
        count += 1  # 统计输出顶点数
        e = ALG.adjList[gettop].firstEdge
        while e:  # 对此顶点弧表遍历
            k = e.adjVex
            ALG.adjList[k].inDgree -= 1  # 将k号顶点邻接点的入度减1
            if not ALG.adjList[k].inDgree:  # 若入度为0则入栈，以便下次循环输出
                stack.Enstack(k)
            e = e.next
    if count < ALG.numNodes:  # count小于顶点数，说明存在环
        return "ERROR"
    else:
        return "OK"


if __name__ == '__main__':
    ALG = ALGraph()
    ALG.createALGraph()
    print(ALG.adjList)
    TopologicalSort(ALG)

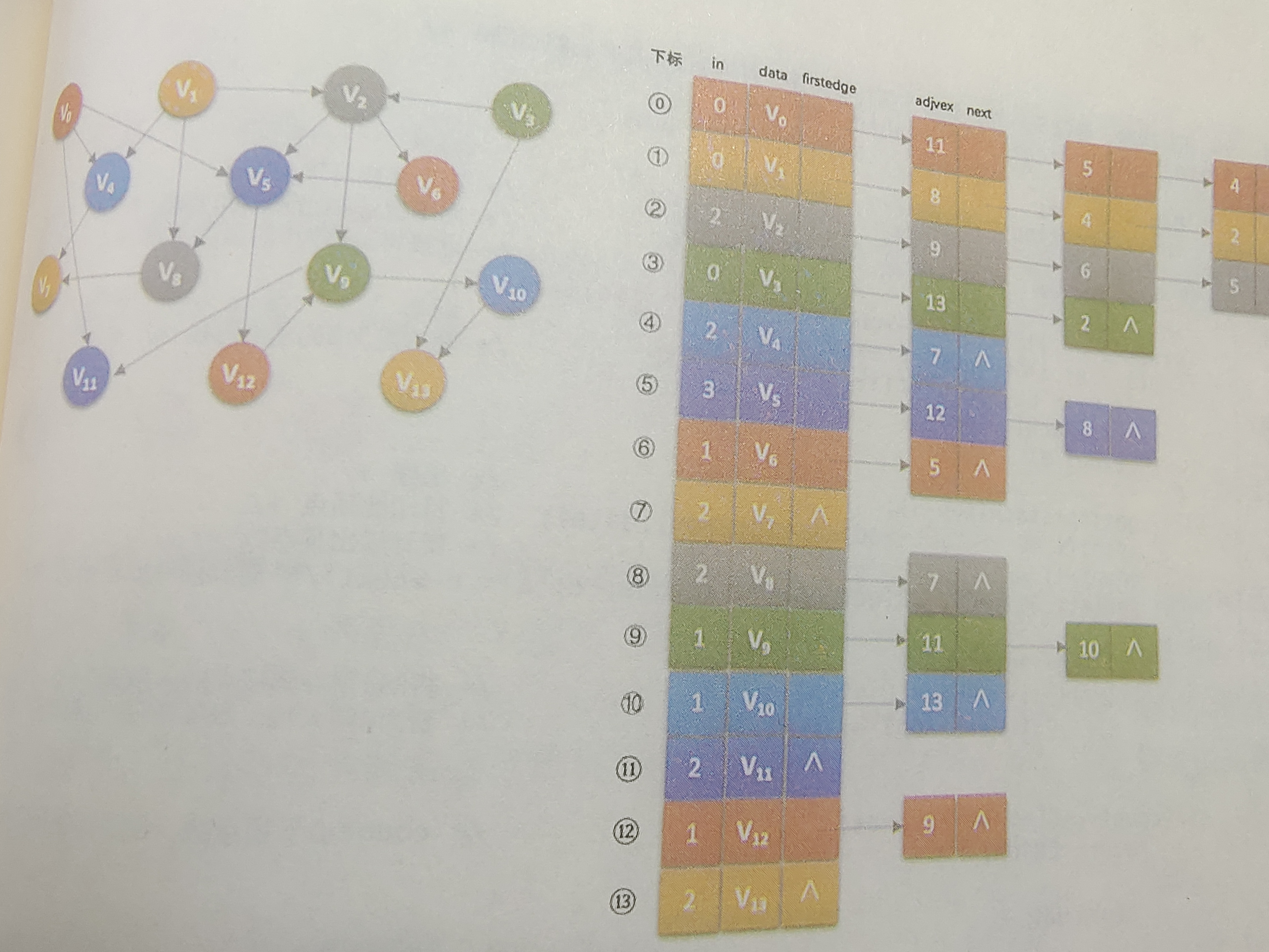
以下面的有向图为例：

运行结果为：

v3 ->v1 ->v2 ->v6 ->v0 ->v4 ->v5 ->v8 ->v7 ->v12 ->v9 ->v11 ->v10 ->v13

本文部分概念和图片来至：https://blog.csdn.net/qq_35644234/article/details/60578189