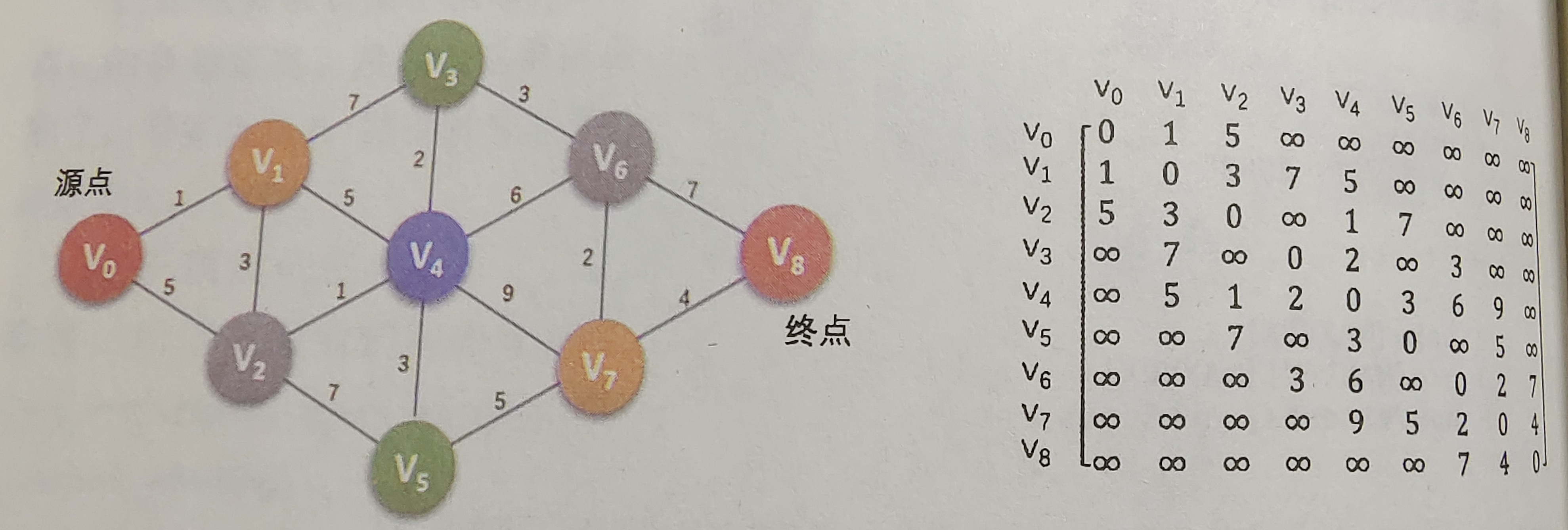
最短路径
对于网图来说,最短路径,是指两顶点之间经过的边上权值之和最少的路径,并且我们称路径上的第一个顶点是源点,最后一个顶点是终点。关于最短路径主要有两种算法,迪杰斯特拉(Dijkstra) 算法和弗洛伊德(Floyd) 算法。
1. 迪杰斯特拉(Dijkstra)算法
对于网N=(V,E),将N中的顶点分成两组:
第一组S:已求出的最短路径的终点集合(初始时只包含源点v0)。
第二组V-S:尚未求出最短路径的终点集合(初始时V-{v0})。
算法将各项顶点与v0 间最短路径长度递增的次序,逐个将集合V-S的顶点加入集合S中去。在这个过程中,总保持从v0到集合S中各顶点的路径长度始终不大于到集合V-S中各顶点x 的路径。
算法的实现要引入以下辅助数据结构:
一位数组S[i]:记录从源点v0到终点vi是否已被确定最短路径长度,true表示确定,false表示尚未确定。
一位数组Path[i]:记录从源点v0到终点vi的当前最短路径上vi的直接前驱顶点序号。其初始值为:如果从v0到vi有弧,则Path[i]为v0,否则为-1。
一位数组D[i]:记录从源点v0到终点vi的当前最短路径长度。其初始值为:如果从v0到vi有弧,则D[i]为弧上的权值,否则为∞。
显然,长度最短的一条最短路径必为(v0,vk),满足以下条件:
D[k] = Min{D[i]|vi∈V-S}
求得顶点vk的最短路径后,将其加入到第一组顶点集S中。
每当加入一个新的顶点到顶点集S,对第二组剩余的各个顶点而言,多一个中转顶点,从而多一个中转路径,所以要对第二组剩余的各个顶点的最短路径长度进行更新。
原来v0到vi的最短路径长度为D[i],加入k作为中间顶点的中转路径长度为:D[k]+Garcs[k][i],若D[k]+Garcs[k][i]<D[i],则用D[k]+Garcs[k][i]取代D[i]。
更新后,再选择数组D中值最小的顶点加入到第一组顶点集S中,如此进行下去,直至图中所有顶点到第一组顶点集S中为止。
python代码实现:
class MGraph():
def __init__(self):
self.vertex = []
self.matrix = []
self.numNodes = 0
self.numEdges = 0
def createMGraph(self):
"""创建无向网图的邻接矩阵表示"""
INFINITY = 65535
self.numNodes = int(input("请输入顶点数:"))
# self.numEdges = int(input("请输入边数:"))
for i in range(self.numNodes):
self.vertex.append(input("请输入一个顶点:"))
for i in range(self.numNodes):
self.matrix.append([])
for j in range(self.numNodes):
if i == j:
self.matrix[i].append(0) # 初始化邻接矩阵
else:
self.matrix[i].append(INFINITY) # 初始化邻接矩阵
# for k in range(self.numEdges): # 读入numEdges条边,建立邻接矩阵
# i = int(input("请输入边(vi,vj)上的下标i:"))
# j = int(input("请输入边(vi,vj)上的下标j:"))
# w = int(input("请输入边(vi,vj)上的权w:"))
# self.matrix[i][j] = w
# self.matrix[j][i] = self.matrix[i][j] # 因为是无向网图,矩阵对称
def viewMGraphStruct(self):
print(self.matrix)
def ShortestPath_Dijkstra(G, v0):
INFINITY = 65535
k = None
Patharc = [-1 for _ in range(G.numNodes)] # 用于存储最短路径下标,并且初始化为-1
ShortPathTable = [G.matrix[v0][v] for v in range(G.numNodes)] # 用于存储到各点最短路径的权值和,初始化:将与v0点有连线的顶点加上权值
final = [0 for _ in range(G.numNodes)] # 定义final并初始化数据,全部顶点初始化为未知最短路径状态,final[w]=1,表示求得顶点v0至vw的最短路径
ShortPathTable[v0] = 0 # v0至v0路径为0
final[v0] = 1 # v0至v0不需要求路径
# 开始主循环,每次求得v0到某个顶点v的最短路径
for v in range(1, G.numNodes):
min = INFINITY # 当前所知离v0顶点最近的距离
for w in range(G.numNodes): # 寻找离v0最近的顶点
if not final[w] and ShortPathTable[w] < min:
k = w
min = ShortPathTable[w] # w顶点里v0顶点更近
final[k] = 1 # 将目前找到的最近的顶点置为1
for w in range(G.numNodes): # 修正当前最短路径及距离
if not final[w] and (min + G.matrix[k][w] < ShortPathTable[w]): # 说明找到了更短的路径,修改Patharc[w] =
# k和ShortPathTable[w]
ShortPathTable[w] = min + G.matrix[k][w] # 修改当前路径长度
Patharc[w] = k
return Patharc, ShortPathTable
if __name__ == '__main__':
G = MGraph()
G.createMGraph()
G.matrix[0][1] = 1
G.matrix[0][2] = 5
G.matrix[1][0] = 1
G.matrix[1][2] = 3
G.matrix[1][3] = 7
G.matrix[1][4] = 5
G.matrix[2][0] = 5
G.matrix[2][1] = 3
G.matrix[2][4] = 1
G.matrix[2][5] = 7
G.matrix[3][1] = 7
G.matrix[3][4] = 2
G.matrix[3][6] = 3
G.matrix[4][1] = 5
G.matrix[4][2] = 1
G.matrix[4][3] = 2
G.matrix[4][5] = 3
G.matrix[4][6] = 6
G.matrix[4][7] = 9
G.matrix[5][2] = 7
G.matrix[5][4] = 3
G.matrix[5][7] = 5
G.matrix[6][3] = 3
G.matrix[6][4] = 6
G.matrix[6][7] = 2
G.matrix[6][8] = 7
G.matrix[7][4] = 9
G.matrix[7][5] = 5
G.matrix[7][6] = 2
G.matrix[7][8] = 4
G.matrix[8][6] = 7
G.matrix[8][7] = 4
v0 = 0
P, D = ShortestPath_Dijkstra(G, v0)
print("最短路径倒序如下:")
for i in range(1, G.numNodes):
print("v{} - v{}: ".format(v0, i), end="")
j = i
while P[j] != -1:
print("{} ".format(P[j]), end="")
j = P[j]
print("\n")
print("源点到各顶点的最短路径长度为:")
for i in range(1, G.numNodes):
print("{} - {} : {}".format(G.vertex[0], G.vertex[i], D[i]))
以下面的网图为例:
运行结果如下:
最短路径倒序如下:
v0 - v1:
v0 - v2: 1
v0 - v3: 4 2 1
v0 - v4: 2 1
v0 - v5: 4 2 1
v0 - v6: 3 4 2 1
v0 - v7: 6 3 4 2 1
v0 - v8: 7 6 3 4 2 1
源点到各顶点的最短路径长度为:
v0 - v1 : 1
v0 - v2 : 4
v0 - v3 : 7
v0 - v4 : 5
v0 - v5 : 8
v0 - v6 : 10
v0 - v7 : 12
v0 - v8 : 16
代码中注释掉的代码是为了测试的时候更加方便,所以用入口函数里的大串赋值代码给代替了,这样就不用每次运行代码都要输入起点,终点和权值了。
时间复杂度分析:由代码的循环嵌套可以轻松得到此算法的时间复杂度为:O(n2)
2.弗洛伊德(Floyd)算法
弗洛伊德算法是基于动态规划算法实现的,接下来我们以在下图所示的有向加权图中查找各个顶点之间的最短路径为例,讲解弗洛伊德算法的实现思路。
[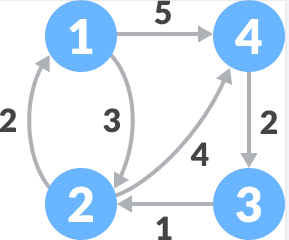
图 1 中不存在环路,且所有路径(边)的权值都为正数,因此可以使用弗洛伊德算法。
弗洛伊德算法查找图 1 中各个顶点之间的最短路径,实现过程如下:
- 建立一张表格,记录每个顶点直达其它所有顶点的权值:
| 目标顶点 | ||||
|---|---|---|---|---|
| 起始顶点 | 1 | 2 | 3 | 4 |
| 1 | 0 | 3 | ∞ | 5 |
| 2 | 2 | 0 | ∞ | 4 |
| 3 | ∞ | 1 | 0 | ∞ |
| 4 | ∞ | ∞ | 2 | 0 |
起始顶点指的是从哪个顶点出发,目标顶点指的是要达到的顶点,例如 2->1 路径的权值是 2,顶点 2 是起始顶点,顶点 1 是目标顶点。此外,∞ 表示无穷大的数,即顶点之间不存在直达的路径。
- 在表 1 的基础上,将顶点 1 作为 "中间顶点",计算从各个顶点出发途径顶点 1 再到达其它顶点的权值,如果比表 1 中记录的权值更小,证明两个顶点之间存在更短的路径,对表 1 进行更新。
从各个顶点出发,途径顶点 1 再到达其它顶点的路径以及对应的权值分别是:
- 2-1-3:权值为 2 + ∞ = ∞,表 1 中记录的 2-3 的权值也是 ∞;
- 2-1-4:权值为 2 + 5 = 7,表 1 中记录的 2-4 的权值是 4;
- 3-1-2:权值为 ∞ + 3,表 1 中记录的 3-2 的权值是 1;
- 3-1-4:权值为 ∞ + 5,表 1 中记录的 3-4 的权值是 ∞;
- 4-1-2:权值为 ∞ + 3,表 1 中记录的 4-2 的权值是 ∞;
- 4-1-3:权值为 ∞ + ∞,表 1 中记录的 4-3 的权值是 2。
以上所有的路径中,没有比表 1 中记录的权值最小的路径,所以不需要对表 1 进行更新。
- 在表 1 的基础上,以顶点 2 作为 "中间顶点",计算从各个顶点出发途径顶点 2 再到达其它顶点的权值:
- 1-2-3:权值为 3 + ∞,表 1 中记录的 1-3 的权值为 ∞;
- 1-2-4:权值为 3 + 4 = 7,表 1 中 1-4 的权值为 5;
- 3-2-1:权值为 1 + 2 = 3,表 1 中 3-1 的权值为 ∞,3 < ∞;
- 3-2-4:权值为 1 + 4 = 5,表 1 中 3-4 的权值为 ∞,5 < ∞;
- 4-2-1:权值为 ∞ + 2,表 1 中 4-1 的权值为 ∞;
- 4-2-3:权值为 ∞ + ∞,表 1 中 4-3 的权值为 2。
以顶点 2 作为 "中间顶点",我们找到了比 3-1、3-4 更短的路径,对表 1 进行更新:
| 目标顶点 | ||||
|---|---|---|---|---|
| 起始顶点 | 1 | 2 | 3 | 4 |
| 1 | 0 | 3 | ∞ | 5 |
| 2 | 2 | 0 | ∞ | 4 |
| 3 | 3(3-2-1) | 1 | 0 | 5(3-2-4) |
| 4 | ∞ | ∞ | 2 | 0 |
- 在表 2 的基础上,将顶点 3 作为 "中间顶点",计算从各个顶点出发途径顶点 3 再到达其它顶点的权值:
- 1-3-2 权值为 ∞ + 1,表 2 中 1-2 的权值为 3;
- 1-3-4 权值为 ∞ + 5,表 2 中 1-4 的权值为 5;
- 2-3-1 权值为 ∞ + 3,表 2 中 2-1 的权值为 2;
- 2-3-4 权值为 ∞ + 5,表 2 中 2-4 的权值为 4;
- 4-3-1 权值为 2 + 3 = 5,表 2 中 4-1 的权值为 ∞,5 < ∞;
- 4-3-2 权值为 2 + 1 = 3,表 2 中 4-2 的权值为 ∞,3 < ∞;
以顶点 3 作为 "中间顶点",我们找到了比 4-1、4-2 更短的路径,对表 2 进行更新:
| 目标顶点 | ||||
|---|---|---|---|---|
| 起始顶点 | 1 | 2 | 3 | 4 |
| 1 | 0 | 3 | ∞ | 5 |
| 2 | 2 | 0 | ∞ | 4 |
| 3 | 3(3-2-1) | 1 | 0 | 5(3-2-4) |
| 4 | 5(4-3-2-1) | 3(4-3-2) | 2 | 0 |
- 在表 3 的基础上,将顶点 4 作为 "中间顶点",计算从各个顶点出发途径顶点 4 再到达其它顶点的权值:
- 1-4-2 权值为 5 + 3 = 8,表 3 中 1-2 的权值为 3;
- 1-4-3 权值为 5 + 2 = 7,表 3 中 1-3 的权值为 ∞,7 < ∞;
- 2-4-1 权值为 4 + 5 = 9,表 3 中 2-1 的权值为 2;
- 2-4-3 权值为 4 + 2 = 6,表 3 中 2-3 的权值为 ∞,6 < ∞;
- 3-4-1 权值为 4 + 5 = 9,表 3 中 3-1 的权值为 3;
- 3-4-2 权值为 5 + 5 = 10 ,表 3 中 3-2 的权值为 1。
以顶点 4 作为 "中间顶点",我们找到了比 1-3、2-3 更短的路径,对表 3 进行更新:
| 目标顶点 | ||||
|---|---|---|---|---|
| 起始顶点 | 1 | 2 | 3 | 4 |
| 1 | 0 | 3 | 7(1-4-3) | 5 |
| 2 | 2 | 0 | 6(2-4-3) | 4 |
| 3 | 3(3-2-1) | 1 | 0 | 5(3-2-4) |
| 4 | 5(4-3-2-1) | 3(4-3-2) | 2 | 0 |
通过将所有的顶点分别作为“中间顶点”,最终得到的表 4 就记录了各个顶点之间的最短路径。例如,4-1 的最短路径为 4-3-2-1。
算法的python实现:
class MGraph():
def __init__(self):
self.vertex = []
self.matrix = []
self.numNodes = 0
self.numEdges = 0
def createMGraph(self):
"""创建无向网图的邻接矩阵表示"""
INFINITY = 65535
self.numNodes = int(input("请输入顶点数:"))
# self.numEdges = int(input("请输入边数:"))
for i in range(self.numNodes):
self.vertex.append(input("请输入一个顶点:"))
for i in range(self.numNodes):
self.matrix.append([])
for j in range(self.numNodes):
if i == j:
self.matrix[i].append(0) # 初始化邻接矩阵
else:
self.matrix[i].append(INFINITY) # 初始化邻接矩阵
# for k in range(self.numEdges): # 读入numEdges条边,建立邻接矩阵
# i = int(input("请输入边(vi,vj)上的下标i:"))
# j = int(input("请输入边(vi,vj)上的下标j:"))
# w = int(input("请输入边(vi,vj)上的权w:"))
# self.matrix[i][j] = w
# self.matrix[j][i] = self.matrix[i][j] # 因为是无向网图,矩阵对称
def viewMGraphStruct(self):
print(self.matrix)
def ShortestPath_Floyd(G):
ShortestPathTable = [[0] * G.numNodes for _ in range(G.numNodes)]
Patharc = [[0] * G.numNodes for _ in range(G.numNodes)]
for v in range(G.numNodes):
for w in range(G.numNodes):
ShortestPathTable[v][w] = G.matrix[v][w]
Patharc[v][w] = w
for k in range(G.numNodes):
for v in range(G.numNodes):
for w in range(G.numNodes):
if ShortestPathTable[v][w] > ShortestPathTable[v][k] + ShortestPathTable[k][w]:
ShortestPathTable[v][w] = ShortestPathTable[v][k] + ShortestPathTable[k][w]
Patharc[v][w] = Patharc[v][k]
print("各顶点间最短路径如下:")
for v in range(G.numNodes):
for w in range(v + 1, G.numNodes):
print("v{} - v{} weight: {}".format(v, w, ShortestPathTable[v][w]), end="")
k = Patharc[v][w]
print(" path: {}".format(v),end="")
while k != w:
print(" -> {}".format(k),end="")
k = Patharc[k][w]
print(" -> {}".format(w))
print("\n")
if __name__ == '__main__':
G = MGraph()
G.createMGraph()
G.matrix[0][1] = 1
G.matrix[0][2] = 5
G.matrix[1][0] = 1
G.matrix[1][2] = 3
G.matrix[1][3] = 7
G.matrix[1][4] = 5
G.matrix[2][0] = 5
G.matrix[2][1] = 3
G.matrix[2][4] = 1
G.matrix[2][5] = 7
G.matrix[3][1] = 7
G.matrix[3][4] = 2
G.matrix[3][6] = 3
G.matrix[4][1] = 5
G.matrix[4][2] = 1
G.matrix[4][3] = 2
G.matrix[4][5] = 3
G.matrix[4][6] = 6
G.matrix[4][7] = 9
G.matrix[5][2] = 7
G.matrix[5][4] = 3
G.matrix[5][7] = 5
G.matrix[6][3] = 3
G.matrix[6][4] = 6
G.matrix[6][7] = 2
G.matrix[6][8] = 7
G.matrix[7][4] = 9
G.matrix[7][5] = 5
G.matrix[7][6] = 2
G.matrix[7][8] = 4
G.matrix[8][6] = 7
G.matrix[8][7] = 4
ShortestPath_Floyd(G)
以下面的网图为例:
运行结果如下:
各顶点间最短路径如下:
v0 - v1 weight: 1 path: 0 -> 1
v0 - v2 weight: 4 path: 0 -> 1 -> 2
v0 - v3 weight: 7 path: 0 -> 1 -> 2 -> 4 -> 3
v0 - v4 weight: 5 path: 0 -> 1 -> 2 -> 4
v0 - v5 weight: 8 path: 0 -> 1 -> 2 -> 4 -> 5
v0 - v6 weight: 10 path: 0 -> 1 -> 2 -> 4 -> 3 -> 6
v0 - v7 weight: 12 path: 0 -> 1 -> 2 -> 4 -> 3 -> 6 -> 7
v0 - v8 weight: 16 path: 0 -> 1 -> 2 -> 4 -> 3 -> 6 -> 7 -> 8
v1 - v2 weight: 3 path: 1 -> 2
v1 - v3 weight: 6 path: 1 -> 2 -> 4 -> 3
v1 - v4 weight: 4 path: 1 -> 2 -> 4
v1 - v5 weight: 7 path: 1 -> 2 -> 4 -> 5
v1 - v6 weight: 9 path: 1 -> 2 -> 4 -> 3 -> 6
v1 - v7 weight: 11 path: 1 -> 2 -> 4 -> 3 -> 6 -> 7
v1 - v8 weight: 15 path: 1 -> 2 -> 4 -> 3 -> 6 -> 7 -> 8
v2 - v3 weight: 3 path: 2 -> 4 -> 3
v2 - v4 weight: 1 path: 2 -> 4
v2 - v5 weight: 4 path: 2 -> 4 -> 5
v2 - v6 weight: 6 path: 2 -> 4 -> 3 -> 6
v2 - v7 weight: 8 path: 2 -> 4 -> 3 -> 6 -> 7
v2 - v8 weight: 12 path: 2 -> 4 -> 3 -> 6 -> 7 -> 8
v3 - v4 weight: 2 path: 3 -> 4
v3 - v5 weight: 5 path: 3 -> 4 -> 5
v3 - v6 weight: 3 path: 3 -> 6
v3 - v7 weight: 5 path: 3 -> 6 -> 7
v3 - v8 weight: 9 path: 3 -> 6 -> 7 -> 8
v4 - v5 weight: 3 path: 4 -> 5
v4 - v6 weight: 5 path: 4 -> 3 -> 6
v4 - v7 weight: 7 path: 4 -> 3 -> 6 -> 7
v4 - v8 weight: 11 path: 4 -> 3 -> 6 -> 7 -> 8
v5 - v6 weight: 7 path: 5 -> 7 -> 6
v5 - v7 weight: 5 path: 5 -> 7
v5 - v8 weight: 9 path: 5 -> 7 -> 8
v6 - v7 weight: 2 path: 6 -> 7
v6 - v8 weight: 6 path: 6 -> 7 -> 8
v7 - v8 weight: 4 path: 7 -> 8
代码中注释掉的代码是为了测试的时候更加方便,所以用入口函数里的大串赋值代码给代替了,这样就不用每次运行代码都要输入起点,终点和权值了。
时间复杂度分析:回头看看弗洛伊德算法,他的代码简洁到就是一个二重循环初始化加一个三重循环权值修正,就完成了所有顶点到所有顶点的最短路径计算。当然开头还有两个推导式用到了循环,这是因为python无法在定义列表的时候定义它的长度,如果不定义他的长度或规模,那么接下来初始化的时候就会出现越界,如果用的c语言那么这两个循环就没了。如此简单的实现,真是巧妙至极,在我看来这是非常漂亮的算法,代码看起来比Dijkstra算法简单多了,也更好理解,但是很可惜由于它的三成嵌套,因此它的时间复杂度是O(n3),如果你面临需要求所有顶点至所有顶点的最短路径问题时,弗洛伊德算法应该是不错的选择。