图的存储结构
(1) 邻接矩阵
图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组（称为邻接矩阵）存储图中的边或弧的信息。设图G有n个顶点，则邻接矩阵是一个nxn的方阵，定义为:
如下无向图：
如下有向图：
我们知道，每条边上带有权的图叫做网，如果要将这些权值保存下来，可以采用权值代替矩阵中的0、1，权值不存在的元素之间用∞表示，如下图，左图是一个有向网图，右图就是它的邻接矩阵。
邻接矩阵结构：
typedef char VerTexType; /* 顶点类型应由用户定义 */
typedef int EdgeType; /* 边上的权值类型应由用户定义 */
#define MAXVEX 100 /* 最大顶点数，应由用户定义 */
#define INFINITY 65535 /* 用65535来替代无穷大 */
typedef struct{
VertexType vexs[MAXVEX]; /* 顶点表 */
EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵，可看作边表 */
int numNodes, numEdges; /* 图中当前的顶点数和边数 */
}MGraph;
采用邻接矩阵表示法创建无向网
(1) 输入总顶点数和总边数。
(2) 依次输入点的信息存入顶点表中。
(3) 初始化邻接矩阵，使每个权值初始化为极大值。
(4)构造邻接矩阵。依次输入每条边依附的顶点和其权值。确定两个顶点在图中的位置之后，使相应的边赋予相应的权值，同时使其堆成边赋予相同的权值。
该算法的时间复杂度为O(n*n)
C语言实现创建无向网G
void CreateMGraph(MGraph *G)
{//采用邻接矩阵表示法，创建无向网G
int i,j,k,w;
printf("输入顶点数和边数:\n");
scanf("%d,%d",&G->numNodes,&G->numEdges); //输入顶点数和边数
for(i=0;i<G->numNodes;++i)
{
scanf(&G->vexs[i])//依次输入点的信息
}
for(=0;i<G->numNodes;++i)
for(j=0;j<G->numNodes;j++)
G->arc[i][j] = INFINITY;//初始化邻接矩阵，边的权值均置为最大值MaxInt
for(k=0;k<G->numEdges;++k) //构造邻接矩阵
{
printf("输入边(vi,vj)上的下标i,下标j和权w:\n");
scanf("%d,%d,%d",&i,&j,&w)//输入一条边依附的顶点及权值
G->arc[i][j] = w;
G->arc[j][i] = G->arc[i][j] ;
}
return OK;
}
python实现无向网G
class MGraph():
def __init__(self):
self.vertex = []
self.matrix = []
self.numNodes = 0
self.numEdges = 0
def createMGraph(self):
"""创建无向网图的邻接矩阵表示"""
self.numNodes = int(input("请输入顶点数："))
self.numEdges = int(input("请输入边数："))
for i in range(self.numNodes):
self.vertex.append(input("请输入一个顶点："))
for i in range(self.numNodes):
self.matrix.append([])
for j in range(self.numNodes):
if i == j:
self.matrix[i].append(0) # 初始化邻接矩阵
else:
self.matrix[i].append("∞") # 初始化邻接矩阵
for k in range(self.numEdges): # 读入numEdges条边，建立邻接矩阵
i = int(input("请输入边(vi,vj)上的下标i:"))
j = int(input("请输入边(vi,vj)上的下标j:"))
w = int(input("请输入边(vi,vj)上的权w:"))
self.matrix[i][j] = w
self.matrix[j][i] = self.matrix[i][j] # 因为是无向网图，矩阵对称
def viewMGraphStruct(self):
print(self.matrix)
if __name__ == '__main__':
G = MGraph()
G.createMGraph()
G.viewMGraphStruct()
以下图无向图为例，把他改为网图，设w01=2,w02=9,w03=6,w12=5,w23=8:
运行结果如下：
[[0, 2, 9, 6],
[2, 0, 5, '∞'],
[9, 5, 0, 8],
[6, '∞', 8, 0]]
从代码中可以看出，n个顶点和e条边的无向网图的创建，时间复杂度为O(n + n2 + e),其中对邻接矩阵的初始化耗费了O(n2)的时间。
邻接矩阵表示法的优缺点
优点：
（1） 便于判断两个顶点之间是否有 边，即根据Aij= 0或1来判断。
（2） 便于 计算各顶点的度。对于无向图，邻接矩阵的第i行元素之和就是顶点i的度。对于有向图，第i行元素之和就是顶点i的出度，第i列元素之和就是顶点i的入度。
缺点：
（1） 不便于增加删除顶点。
（2） 空间复杂度高。如果是有向图，n个顶点需要nn个单元存储边。如果无向图，其邻接矩阵是对称的，所以对规模较大的邻接矩阵可以采用压缩存储的方法，仅存储下三角元素，这样需要n(n-1)/2个单元。无论哪种存储方式，邻接矩阵表示法的空间复杂度均为0(nn)
(2) 邻接表
数组与链表相结合的存储方法称为邻接表。
1.图中顶点用一个一维数组存储，当然，顶点也可以用单链表来存储，不过数组可以较容易地读取顶点信息，更加方便。另外，对于顶点数组中，每个数据元素还需要存储指向第一个邻接点的指针，以便于查找该顶点的边信息。2.图中每个顶点vi的所有邻接点构成一个线性表，由于邻接点的个数不定，所以用单链表存储，无向图称为顶点vi 的边表，有向图则称为顶点vi作为弧尾的出边表。
如图是一个无向图的连接表结构，有向图则类似。
对于带权值的网图，可以在边表结点定义中再增加一个weight 的数据域，存储权值信息即可，如下图所示。
图的邻接表存储表示
#define MAXVEX 100 //最大顶点数
typedef char VertexType; /* 顶点类型应由用户定义 */
typedef int EdgeType; /* 边上的权值类型应由用户定义 */
typedef struct EdgeNode /* 边表结点 */
{
int adjvex; /* 邻接点域,存储该顶点对应的下标 */
EdgeType info; /* 用于存储权值,对于非网图可以不需要 */
struct EdgeNode *next; /* 链域,指向下一个邻接点 */
}EdgeNode;
typedef struct VertexNode /* 顶点表结点 */
{
VertexType data; /* 顶点域,存储顶点信息 */
EdgeNode *firstedge;/* 指向第一条依附顶点的边指针 */
}VertexNode, AdjList[MAXVEX];
typedef struct{
AdjList adjList;
int numNodes,numEdges; /* 图中当前顶点数和边数 */
}GraphAdList;
采用邻接表表示法创建无向图
(1)输入总顶点数和总边数
(2)依次输入点的信息存入顶点表中，使每个表头结点的指针域初始化为NULL。
(3) 创建邻接表。依次输入每条边依附的两个顶点，确定这两个顶点的序号i和j之后，将此边结点分别插入vi 和vj对应的两个链表的头部。
该算法的时间复杂度为O（n+e）
c语言实现
void CreateALGraph(GraphAdList *G)
{
int i,j,k;
EdgeNode *e;
printf("输入顶点数和边数：\n");
scanf("%d,%d",&G->numNodes,&G->numEdges);//输入总顶点数，总边数
for(i=0;i<G->numNodes;i++)//输入各点，构造表头结点表
{
scanf(&G->adjList[i].data);//输入顶点值
G->adjList[i].firstedge = NULL；//初始化表头结点的指针域为NULL
}
for(k=0;k<G->numEdges;k++)//输入各边，构造邻接表
{
printf("输入边(vi,vj)上的顶点序号：\n");
scanf("%d,%d",&i,&j);
e = (EdgeNode·*)malloc(sizeof(EdgeNode));
e->adjvex = j;
e->next = G->adjList[i].firstedge;
G->adjList[i].firstedge = e;
e = (EdgeNode·*)malloc(sizeof(EdgeNode));
e->adjvex = i;
e->next = G->adjList[j].firstedge;
G->adjList[j].firstedge = e;
}
}
python实现
class Vertex(object):
"""创建Vertex类，用来存放顶点信息（包括data和firstEdge）"""
def __init__(self, data=None):
self.data = data
self.firstEdge = None
class EdgeNode(object):
""" 创建Edge类，用来存放边信息（包括adjVex和next）；"""
def __init__(self, adjVex):
self.adjVex = adjVex
self.next = None
class ALGraph():
"""无向图类"""
def __init__(self):
self.numNodes = 0
self.numEdges = 0
self.adjList = []
def createALGraph(self):
self.numNodes = int(input("输入顶点数："))
self.numEdges = int(input("输入边数："))
for i in range(self.numNodes): # 读入顶点信息，建立顶点表
v = Vertex()
self.adjList.append(v)
self.adjList[i].data = input("请输入顶点数据：")
for k in range(self.numEdges): # 建立边表
i = int(input("请输入边(vi,vj)上的下标i："))
j = int(input("请输入边(vi,vj)上的下标j："))
e = EdgeNode(j) # 实例化边节点
e.next = self.adjList[i].firstEdge # 将e的指针指向当前顶点指向的节点
self.adjList[i].firstEdge = e # 将当前顶点的指针指向e
e = EdgeNode(i) # 实例化边节点
e.next = self.adjList[j].firstEdge # 将e的指针指向当前顶点指向的节点
self.adjList[j].firstEdge = e # 将当前顶点的指针指向e
if __name__ == '__main__':
G = ALGraph()
G.createALGraph()
print(G.adjList)
以下图无向图为例：
程序运行结果如下：
输入顶点数：4
输入边数：5
请输入顶点数据：v0
请输入顶点数据：v1
请输入顶点数据：v2
请输入顶点数据：v3
请输入边(vi,vj)上的下标：i0
请输入边(vi,vj)上的下标：j1
请输入边(vi,vj)上的下标：i0
请输入边(vi,vj)上的下标：j2
请输入边(vi,vj)上的下标：i0
请输入边(vi,vj)上的下标：j3
请输入边(vi,vj)上的下标：i1
请输入边(vi,vj)上的下标：j2
请输入边(vi,vj)上的下标：i2
请输入边(vi,vj)上的下标：j3
[<__main__.Vertex object at 0x0000022255DAE040>, <__main__.Vertex object at 0x0000022255C17730>, <__main__.Vertex object at 0x0000022255C17640>, <__main__.Vertex object at 0x0000022255D65E50>]
这里使用了单链表创建中的头插法，对于无向图，一条边都是对应两个顶点，所以在循环中，一次就针对i和j分别进行了插入。本算法的时间复杂度，对于n个顶点e条边来说，很容易得出是O(n + e)。
邻接表表示法的优缺点
优点：
（1） 便于增加和删除结点。
（2） 便于统计边的数目，按顶点表顺序扫描所有边表可得到边的数目，时间复杂度为O(n+e)。
（3）空间效率高。对于一个具有n个顶点e条边的图G，若图G是无向图，则在邻接表表示中有n个顶点表结点和2n个边表结点。若G是有向图，则在它的邻接表表示或逆邻接表表示中均有n个顶点表结点和e个边表结点。因此，邻接表的空间复杂度为O(n+e)。
缺点：
（1） 不便于判断顶点之间是否有边，要判断vi 和vj之间是否有边，就需扫描第i个边表，最换情况下要耗费O(n)时间。
（2） 不便于计算有向图各个顶点的度。
(3) 十字链表
与邻接表不同，十字链表法仅适用于存储有向图和有向网。不仅如此，十字链表法还改善了邻接表计算图中顶点入度的问题。
十字链表存储有向图（网）的方式与邻接表有一些相同，都以图（网）中各顶点为首元节点建立多条链表，同时为了便于管理，还将所有链表的首元节点存储到同一数组或链表中。
其中，建立个各个链表中用于存储顶点的首元节点结构如图所示：
从图 可以看出，首元节点中有一个数据域和两个指针域（分别用 firstin 和 firstout 表示)：
- firstin 指针用于连接以当前顶点为弧头的其他顶点构成的链表；
- firstout 指针用于连接以当前顶点为弧尾的其他顶点构成的链表；
- data 用于存储该顶点中的数据；
由此可以看出，十字链表实质上就是为每个顶点建立两个链表，分别存储以该顶点为弧头的所有顶点和以该顶点为弧尾的所有顶点。
注意，存储图的十字链表中，各链表中首元节点与其他节点的结构并不相同，图 1 所示仅是十字链表中首元节点的结构，链表中其他普通节点的结构如图所示：
从图 2 中可以看出，十字链表中普通节点的存储分为 5 部分内容，它们各自的作用是：
- tailvex 用于存储以首元节点为弧尾的顶点位于数组中的位置下标；
- headvex 用于存储以首元节点为弧头的顶点位于数组中的位置下标；
- hlink 指针：用于链接下一个存储以首元节点为弧头的顶点的节点；
- tlink 指针：用于链接下一个存储以首元节点为弧尾的顶点的节点；
- info 指针：用于存储与该顶点相关的信息，例如量顶点之间的权值；
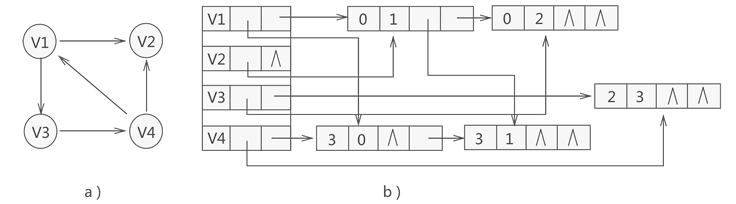
比如说，用十字链表存储图 a) 中的有向图，存储状态如图 b) 所示：
拿图 中的顶点 V1 来说，通过构建好的十字链表得知，以该顶点为弧头的顶点只有存储在数组中第 3 位置的 V4（因此该顶点的入度为 1），而以该顶点为弧尾的顶点有两个，分别为存储数组第 1 位置的 V2 和第 2 位置的 V3（因此该顶点的出度为 2）。
对于图中各个链表中节点来说，由于表示的都是该顶点的出度或者入度，因此没有先后次序之分。
图 3 中十字链表的构建过程转化为 C 语言代码为：
#define MAX_VERTEX_NUM 20
#define InfoType int//图中弧包含信息的数据类型
#define VertexType int
typedef struct ArcBox{
int tailvex,headvex;//弧尾、弧头对应顶点在数组中的位置下标
struct ArcBox *hlik,*tlink;//分别指向弧头相同和弧尾相同的下一个弧
InfoType *info;//存储弧相关信息的指针
}ArcBox;
typedef struct VexNode{
VertexType data;//顶点的数据域
ArcBox *firstin,*firstout;//指向以该顶点为弧头和弧尾的链表首个结点
}VexNode;
typedef struct {
VexNode xlist[MAX_VERTEX_NUM];//存储顶点的一维数组
int vexnum,arcnum;//记录图的顶点数和弧数
}OLGraph;
int LocateVex(OLGraph * G,VertexType v){
int i=0;
//遍历一维数组，找到变量v
for (; i<G->vexnum; i++) {
if (G->xlist[i].data==v) {
break;
}
}
//如果找不到，输出提示语句，返回 -1
if (i>G->vexnum) {
printf("no such vertex.\n");
return -1;
}
return i;
}
//构建十字链表函数
void CreateDG(OLGraph *G){
//输入有向图的顶点数和弧数
scanf("%d,%d",&(G->vexnum),&(G->arcnum));
//使用一维数组存储顶点数据，初始化指针域为NULL
for (int i=0; i<G->vexnum; i++) {
scanf("%d",&(G->xlist[i].data));
G->xlist[i].firstin=NULL;
G->xlist[i].firstout=NULL;
}
//构建十字链表
for (int k=0;k<G->arcnum; k++) {
int v1,v2;
scanf("%d,%d",&v1,&v2);
//确定v1、v2在数组中的位置下标
int i=LocateVex(G, v1);
int j=LocateVex(G, v2);
//建立弧的结点
ArcBox * p=(ArcBox*)malloc(sizeof(ArcBox));
p->tailvex=i;
p->headvex=j;
//采用头插法插入新的p结点
p->hlik=G->xlist[j].firstin;
p->tlink=G->xlist[i].firstout;
G->xlist[j].firstin=G->xlist[i].firstout=p;
}
}
提示，代码中新节点的插入采用的是头插法。
(4) 邻接多重表
邻接多重表是无向图的另一种链式存储结构. 虽然邻接表是无向图的一种很有效的存储结构,在邻接表中容易求得顶点和边的各种信息. 但是,在邻接表中每一条边(vi,vj)有两个结点，分别在第i个和第j个链表中，这给某些图的操作带来不便。如对已被搜索过的边作记号或删除一条边等，此时需要找到表示同一条边的两个结点。因此，在进行这类操作的无向图的问题中采用邻接多重表更合适。
邻接多重表的结构和十字链表类型。边结点和顶点结点如下示：
边结点由6个域组成：mark为标志域，可标记这条边是否被搜索过； ivex和jvex为该边依附的两个顶点在图中的位置；ilink指向下一条依附于顶点ivex的边；jlink指向下一条依附于顶点jvex的边，info为指向和边相关的各种信息的指针域。
顶点结点由2个域组成：data存储和该顶点相关的信息如顶点名称；firstedge域指示第一条依附于该顶点的边。
示意图
算法分析
建立邻接多重链表的时间复杂度和建立邻接表是相同的. 另外邻接多重表几乎只针对无向图或无向网。
