JMLR 2019
https://www.jmlr.org/papers/volume20/18-196/18-196.pdf
utilizes simulation to learn structured feature transforms that map the original parameter space into a domain-informed space
During BO, similarity between controllers is now calculated in this transformed space
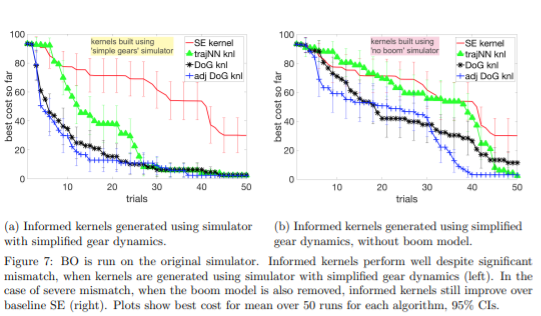
create increasingly approximate simulators and study the effect of increasing simulation-hardware mismatch
additional dim for the gap (trained online)

1 Introduction

robots: costly in real
black-box, non-convex, discontinuous
- PI^2, PILCO, continuous
- CMA-ES, expensive
BO, efficiency degrades in high dimensions

GP, 0, no prior
k, large? strongly influence!
- Squared Exponential, hyperparam
- Matern? we use domain-informed! remove the limitation of stationary
\(u=\pi_x(s)\), trajectory
incorporating simulation

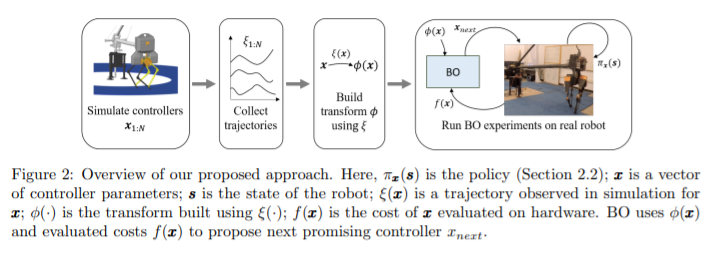
3 Proposed Approach: Bayesian Optimization with Informed Kernels

collect sim traj, build an informed transform ("map")
\(\phi\), form is the same as that of SE kernel
brings controllers that perform similar in simulation closer together, as compared to the original parameter space. For locomotion, this could bring failing controllers close together to occupy only a small portion of the transformed space
In essence, this means that the resultant kernel, though stationary in \(\phi\), is non-stationary in x
learn a feature transform
- traj summary, fall: far away from walk
- Sobol grid, dataset for NN to fit
- NN outputs: kernel for BO
- didn't carefully select the sensory traces

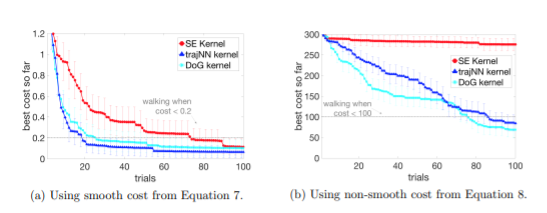
DoG: domain knowledge
gap!
prior-based? biased towards sampling promising points from simulation, bad!
kernel-based? √
- needn't to be re-run for another cost
- less sample-efficient
- easy to generalize
possible to combine

发表于 2021-11-05 16:52 minor_second 阅读(48) 评论(0) 编辑收藏举报