来源:http://blog.sina.com.cn/s/blog_6b1c9ed50101l02a.html,http://wenku.baidu.com/link?url=3mRTbARl0uPHHRFO9CdqhBNeUj-nb8dRwtqRN2oGqu8u1kN6IsqgYy-H8ggB7jOkPXhx703oM9YW9ftfOlh2dz7KJmlliOhDa4-WZFEEus_,http://www.dxy.cn/bbs/thread/28263194#28263194
一、假设检验基础:p-value相关
0. 单个假设检验中主要依靠p值(或统计量t)做出是否拒绝零假设H0的决定:p-value和预先设定的检验水准alpha做对比,如果p-value小于等于alpha,拒绝原假设,否则不拒绝原假设。
1. p-value:表征了在原假设成立的条件下,重复进行当前的试验,获得现有统计量t及其更极端情况的概率。
2. 给定检验水准alpha时,可得出对应的拒绝域;根据当前试验,可以计算出p-value。当p-value越小时,表示此时试验得到的统计量t越落在拒绝域。因此基于p-value的结果等价于基于t值的结果。因此,p-value越小,拒绝原假设的信心越大。
3. 假阳性率:false positive rate, FPR。检验水准alpha给出了事先犯I-型错误的最大概率。
自己重新翻了一下书(《现代教育与心理统计学》,第八章),笔记如下:
· 差异是否显著:从平均数为x0的总体重人意抽取的样本平均数x1(这里为了打字方便就用这两个记号表示了),只要x1落在下图(网络来源)左上非阴影区域,那么就认为当x1与x0不重合时,其的差异是抽样误差所致,即“差异不显著”,此时接受H0。
· alpha(显著性水平)
如果上图左上两边阴影面积加起来占全面积1%,等价于alpha = 0.01。
· 两类错误(假设alpha = 0.01)
Ⅰ型错误(“弃真”):当x1落入阴影面积,我们的错x1与x0差异显著的结论,但与此同时,这个结论也有可能是错的,即有1%的可能犯错。这种错误发生是因为H0本来是正确的,但我们错误地拒绝了它。可以看到Ⅰ型错误的发生概率等于alpha。
Ⅱ型错误(“取伪”):H0本来是错误的,但我们错误地接受了它,此时犯错误的概率,一般记为beta。
==> 为了即以方便,我们只要记住“弃真”“取伪”中的“真”和“伪”都是说H0的,并且行为都是和理论行为相反(“真”时反而抛弃,“伪”时反而接受)。
==> alpha + beta并不等于1,因为两类错误的前提不同:Ⅰ类错误中H0为真,那么所有讨论应当在类似于上图左上的正态分布中讨论;而在Ⅱ类错误中,H0为假等价于H1为真,那么就应当在H1的正态分布中讨论,此时beta和之前的alpha是没有关系的两个量。
==> 统计检验力(1 - beta):如果x1真实值与x0很小,某个检验仍然可以以较大把握接受它,那么就说这个检验的统计检验力很大(即(1 - beta)增大,即beta减小)。
· 单侧检验与双侧检验
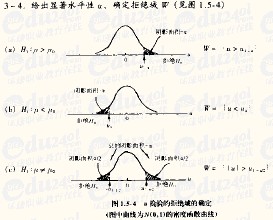 (这图网上搜的...也是醉了)
(这图网上搜的...也是醉了)从上到下依次为右侧(right-tailed)、左侧(left-tailed)以及双侧(two-tailed)检验。
··· 右侧检验(拒绝域在右侧):
H0:μ ≤ μ0,H1:μ > μ0
阴影部分面积:alpha;
··· 左侧检验(拒绝域在左侧):
H0:μ ≥ μ0,H1:μ < μ0
阴影部分面积:alpha;
··· 双侧检验(拒绝域在两侧)
H0:μ = μ0,H1:μ ≠ μ0
阴影部分面积:alpha/2。
==>由以上内容可以看出:alpha一定的情况下,相比于单侧检验,双侧检验的临界点要更远离μ0,即beta增大,即“取伪”错误概率增大。所以一个问题如果可以用单侧检验,就不要用双侧检验。(当然必须用双侧检验的,不要强行用单侧检验)
“一般认为双侧检验较保守和稳妥,而单侧检验由于充分利用了另一侧的不可能性,更易得出有差异性的结论,但应慎用。单侧检验和双侧检验中计算统计量的过程是相同的,先确定概率P值时的‘显著界限值’是不同的。如alpha = 0.05,自由度v = 14,取单侧显著性界限值t = 1.761,而双侧显著界限值t = 2.145,可见单侧检验界值比双侧检验界值小,以为着进行单侧检验时,统计量易达到界限水平,即易得P < 0.05的结论。”
二、多重假设检验和总体错误率
0. 在进行多重假设检验时,每个单独的假设都具有其本身的I型错误。在这种情况下,如果不进行任何的控制,犯I-型错误的概率会随着假设检验的个数而迅速增加。
(严超赣老师在DPARSF的教学视频中对为什么要进行FDR校正进行了详细的举例说明:
“单个体素,p = 0.05,即犯错概率为5%。但如果要对五个体素一起校正,那么犯错误概率就会变成 p = 1 - (0.95)^5 = 0.23。这样的话很容易就会出现“假阳性(false positive)”,即H0被错误拒绝的情况。再换句话说,随着体素数目增多,Ⅰ型错误(“弃真”错误)的概率增大了。但这种情况下,即使出现H0被拒绝,我们也不能说H0为假。为了控制这种情况。最简单的方法是把每个体素p值都减小,例如bonferroni's correction:假设需要所有5个体素犯错误概率为0.05,那么控制每个体素p = 0.05/5 = 0.01。但这种方法太严格,如果体素较多,例如100个,那么控制每个体素p = 0.005已经很难,更别说大脑中动辄上万个体素了。所以我们一般考虑其他更灵活的矫正方式,如FWE、FDR以及AlphaSim。”)
1. 多重假设检验中,广泛使用的错误控制指标是总体错误率(family-wise error rate,FWER),即至少出现一次错误地拒绝真实H0的可能性;FWER小于等于alpha。而研究者更关心的是能否尽量多地识别出差异表达的基因,并且能够容忍和允许总的拒绝中发生少量的错误识别,称为错误发现false discovery。即需要在错误发现和总的拒绝次数R之间寻找一种平衡,即在检验出尽可能多的候选变量的同时将错误发现率控制在一个可以接受的范围。
2. 错误发现率(False Discovery Rate,FDR),表示了在所有R次拒绝中错误发现的期望比例。错误发现率和假阳性率之间有着本质的差别。错误发现率将范围限定在总的拒绝次数中;而假阳性率则针对所有变量数而言。
3. 给定FDR的控制水平alpha,多重假设检验次数M,通过求得拒绝H0的次数N,可得出多重检验M次中,有多少次是被错误识别的(=alpha * N)。Benjamini和Hochberg给出了一个基于p-value的逐步向下控制程序,用于求出拒绝H0的次数N的值。并且证明在BH控制下,FDR 小于等于 alpha。
三、pFDR和q值
0. pFDR阳性错误拒绝率,是基于至少拒绝一个H0的事实。经过一系列的推导,pFDR的实际意义是,在pFDR错误率控制下,当拒绝一个H0时,该假设为真实的概率;pFDR反应了已经在拒绝H0的情况下H0 = 0的概率。可以认为pFDR是贝叶斯后验p值。
1. 按照和p-value类似的定义,Storey给出了q-value的定义。


2. q-value量化了在观察统计量T = t时,拒绝H0所犯的最小pFDR。p-value的定义基于H0=0的条件而量化T属于Talpha的概率,显然q值是p值定义的一个逆过程,q值是基于T属于Talpha的条件而量化H0=0的概率。
3. 和BH控制不同,q值和pFDR正好相反,即通过选定的拒绝域Talpha去估计对应的q值,当q小于等于alpha时,可保证FDr小于等于alpha。Storey给出了关于q值和pFDR的估计算法。
4. 根据p-value或q-value可以计算对应的FDR,多重假设检验中拒绝H0的次数。
5. BH计算错误发现率时具有保守性,即在降低假阳性的同时,也减少了正确的假设。为此可采用q-value用于FDR计算。
在此加入严超赣老师在DPARSF教学视频中对FDR讲解(下图来自于视频PPT):
V:本来无显著差别的“宣布为”有显著差别,即错误判断的个数;R:总共报告有显著差别的个数。
则V/R代表:犯错误的几率。
那么FDR = E(V/R)表示:在所有报告有显著差异的个体中可能误报的比例,即Q value。
举例:Q = 0.05,那么报告了100个显著差异体素,其中最多有5个是实际上无显著差异的。
====================================================================
FDR错误控制法是Benjamini于1995年提出一种方法,通过控制FDR(False Discovery Rate)来决定P值的域值. 假设你挑选了R个差异表达的基因,其中有S个是真正有差异表达的,另外有V个其实是没有差异表达的,是假阳性的。实践中希望错误比例Q=V/R平均而言不能超过某个预先设定的值(比如0.05),在统计学上,这也就等价于控制FDR不能超过5%.
对所有候选基因的p值进行从小到大排序,则若想控制fdr不能超过q,则只需找到最大的正整数i,使得 p(i)<= (i*q)/m.然后,挑选对应p(1),p(2),...,p(i)的基因做为差异表达基因,这样就能从统计学上保证fdr不超过q。因此,FDR的计算公式如下:
q-value(i)=p(i)*length(p)/rank(p)
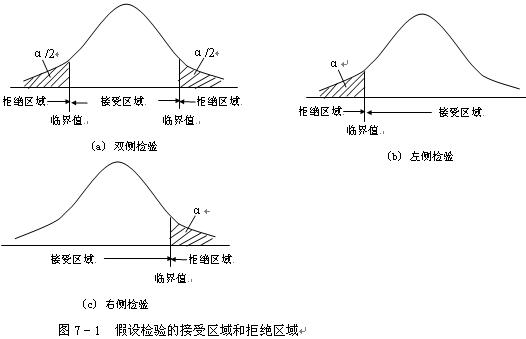
 (这图网上搜的...也是醉了)
(这图网上搜的...也是醉了)






