AB测试】支付宝营销策略效果分析ipynb
参考地址:
【A/B测试】支付宝营销策略效果分析
Programmer: Dan.Q
Date: 2020.06.25
A/B测试常用于比较不同设计、运营方案的优劣,以辅助决策。本分析以支付宝营销活动为例,通过广告点击率指标比较两组营销策略的广告投放效果。
1. 数据来源
本文所用数据集来自阿里云天池:
阿里云天池 - Audience Expansion Dataset
该数据集包含三张表,分别记录了支付宝两组营销策略的活动情况:
- emb_tb_2.csv: 用户特征数据集
- effect_tb.csv: 广告点击情况数据集
- seed_cand_tb.csv: 用户类型数据集
本分析报告主要使用广告点击情况数据,涉及字段如下:
- dmp_id:营销策略编号(源数据文档未作说明,这里根据数据情况设定为1:对照组,2:营销策略一,3:营销策略二)
- user_id:支付宝用户ID
- label:用户当天是否点击活动广告(0:未点击,1:点击)
2. 数据处理
2.1 数据导入和清洗
1. 整合表
# import libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline# load data
data = pd.read_csv('data/effect_tb.csv',header = None)
data.columns = ["dt","user_id","label","dmp_id"]
# 日志天数属性用不上,删除该列
data = data.drop(columns = "dt")
data.head(3)| user_id | label | dmp_id | |
|---|---|---|---|
| 0 | 1 | 0 | 1 |
| 1 | 1000004 | 0 | 1 |
| 2 | 1000004 | 0 | 2 |
# table summary
data.describe()| user_id | label | dmp_id | |
|---|---|---|---|
| count | 2.645958e+06 | 2.645958e+06 | 2.645958e+06 |
| mean | 3.112995e+06 | 1.456297e-02 | 1.395761e+00 |
| std | 1.828262e+06 | 1.197952e-01 | 6.920480e-01 |
| min | 1.000000e+00 | 0.000000e+00 | 1.000000e+00 |
| 25% | 1.526772e+06 | 0.000000e+00 | 1.000000e+00 |
| 50% | 3.062184e+06 | 0.000000e+00 | 1.000000e+00 |
| 75% | 4.721132e+06 | 0.000000e+00 | 2.000000e+00 |
| max | 6.265402e+06 | 1.000000e+00 | 3.000000e+00 |
2. 重复值处理
# shape of df
data.shape(2645958, 3)# distinct count of columns
data.nunique()user_id 2410683
label 2
dmp_id 3
dtype: int64数据行数与独立用户数不统一,检查是否存在重复行:
data[data.duplicated(keep = False)].sort_values(by = ["user_id"])| user_id | label | dmp_id | |
|---|---|---|---|
| 8529 | 1027 | 0 | 1 |
| 1485546 | 1027 | 0 | 1 |
| 1579415 | 1471 | 0 | 1 |
| 127827 | 1471 | 0 | 1 |
| 404862 | 2468 | 0 | 1 |
| ... | ... | ... | ... |
| 1382121 | 6264633 | 0 | 1 |
| 1382245 | 6264940 | 0 | 1 |
| 2575140 | 6264940 | 0 | 1 |
| 1382306 | 6265082 | 0 | 3 |
| 2575171 | 6265082 | 0 | 3 |
25966 rows × 3 columns
# drop duplicate
data = data.drop_duplicates()
# check if any duplicates left
data[data.duplicated(keep = False)]| user_id | label | dmp_id |
|---|
3. 空值处理
# check null values
data.info(null_counts = True)<class 'pandas.core.frame.DataFrame'>
Int64Index: 2632975 entries, 0 to 2645957
Data columns (total 3 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 user_id 2632975 non-null int64
1 label 2632975 non-null int64
2 dmp_id 2632975 non-null int64
dtypes: int64(3)
memory usage: 80.4 MB数据集无空值,无需进行处理。
4. 异常值检查
通过透视表检查各属性字段是否存在不合理取值:
data.pivot_table(index = "dmp_id", columns = "label", values = "user_id",
aggfunc = "count", margins = True)| label | 0 | 1 | All |
|---|---|---|---|
| dmp_id | |||
| 1 | 1881745 | 23918 | 1905663 |
| 2 | 404811 | 6296 | 411107 |
| 3 | 307923 | 8282 | 316205 |
| All | 2594479 | 38496 | 2632975 |
5. 数据类型
data.dtypesuser_id int64
label int64
dmp_id int64
dtype: object数据类型正常,无需处理。
2.2 样本容量检验
在进行A/B测试前,需检查样本容量是否满足试验所需最小值。
这里借助Evan Miller的样本量计算工具:
Sample Size Calculator
首先需要设定点击率基准线以及最小提升比例,我们将对照组的点击率设为基准线.
# click rate of control group
data[data["dmp_id"] == 1]["label"].mean()0.012551012429794775对照组点击率为1.26%,假定我们希望新的营销策略能让广告点击率至少提升1个百分点,则算得所需最小样本量为:2167。 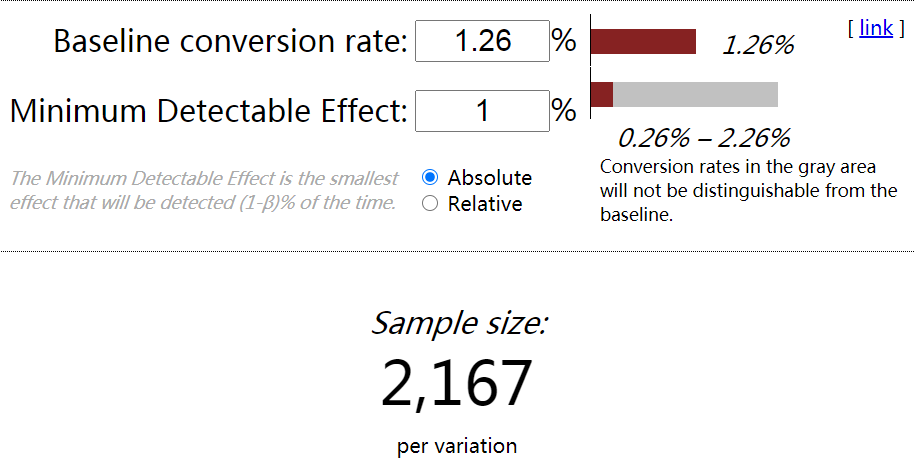
# sample size of campaigns
data["dmp_id"].value_counts()1 1905663
2 411107
3 316205
Name: dmp_id, dtype: int64两组营销活动的样本量分别为41.11万和31.62万,满足最小样本量需求。
# 保存清洗好的数据备用
# save it to file
data.to_csv("data/output.csv", index = False)
# reload data
# data = pd.read_csv("data/output.csv")3. 假设检验
先观察几组试验的点击率情况。
# click rate of groups
print("对 照 组: " ,data[data["dmp_id"] == 1]["label"].mean())
print("营销策略一: " ,data[data["dmp_id"] == 2]["label"].mean())
print("营销策略二: " ,data[data["dmp_id"] == 3]["label"].mean())对 照 组: 0.012551012429794775
营销策略一: 0.015314747742072015
营销策略二: 0.026191869198779274可以看到策略一和策略二相较对照组在点击率上都有不同程度提升。
其中策略一提升0.2个百分点,策略二提升1.3个百分点,只有策略二满足了前面我们对点击率提升最小值的要求。
接下来需要进行假设检验,看策略二点击率的提升是否显著。
a. 零假设和备择假设
记对照组点击率为p1,策略二点击率为p2,则:
零假设 H0: p1 ≥ p2
备择假设 H1: p1 < p2
b. 分布类型、检验类型和显著性水平
样本服从二点分布,独立双样本,样本大小n>30,总体均值和标准差未知,所以采用Z检验。显著性水平α取0.05。
3.1 方法一:公式计算
# 用户数
n_old = len(data[data.dmp_id == 1]) # 对照组
n_new = len(data[data.dmp_id == 3]) # 策略二
# 点击数
c_old = len(data[data.dmp_id ==1][data.label == 1])
c_new = len(data[data.dmp_id ==3][data.label == 1])
# 计算点击率
r_old = c_old / n_old
r_new = c_new / n_new
# 总和点击率
r = (c_old + c_new) / (n_old + n_new)
print("总和点击率:", r)<ipython-input-42-dfc782d19ecb>:6: UserWarning: Boolean Series key will be reindexed to match DataFrame index.
c_old = len(data[data.dmp_id ==1][data.label == 1])总和点击率: 0.014492310074225832<ipython-input-42-dfc782d19ecb>:7: UserWarning: Boolean Series key will be reindexed to match DataFrame index.
c_new = len(data[data.dmp_id ==3][data.label == 1])# 计算检验统计量z
z = (r_old - r_new) / np.sqrt(r * (1 - r)*(1/n_old + 1/n_new))
print("检验统计量z:", z)检验统计量z: -59.44168632985996# 查α=0.05对应的z分位数
from scipy.stats import norm
z_alpha = norm.ppf(0.05)
z_alpha-1.6448536269514729z_alpha = -1.64, 检验统计量z = -59.44,该检验为左侧单尾检验,拒绝域为{z<z_alpha}。
所以我们可以得出结论:原假设不成立,策略二点击率的提升在统计上是显著的。
3.2 方法二:Python函数计算
直接用python statsmodels包计算z值和p值。
import statsmodels.stats.proportion as sp
z_score, p = sp.proportions_ztest([c_old, c_new],[n_old, n_new], alternative = "smaller")
print("检验统计量z:",z_score,",p值:", p)检验统计量z: -59.44168632985996 ,p值: 0.0p值约等于0,p < α,与方法一结论相同,拒绝原假设。
作为补充,我们再检验下策略一的点击率提升是否显著。
# 策略一检验
z_score, p = sp.proportions_ztest([c_old, len(data[data.dmp_id ==2][data.label == 1])],[n_old, len(data[data.dmp_id == 2])], alternative = "smaller")
print("检验统计量z:",z_score,",p值:", p)检验统计量z: -14.165873564308429 ,p值: 7.450121742737582e-46<ipython-input-46-866f7bee4cd0>:2: UserWarning: Boolean Series key will be reindexed to match DataFrame index.
z_score, p = sp.proportions_ztest([c_old, len(data[data.dmp_id ==2][data.label == 1])],[n_old, len(data[data.dmp_id == 2])], alternative = "smaller")p值约等于7.45,p > α,无法拒绝原假设,策略一对广告点击率的提升效果不显著。
4. 结论
综上所述,两种营销策略中,只有策略二对广告点击率有显著提升效果,相较于对照组点击率提升了近一倍,因而在两组营销策略中应选择第二组进行推广。


