统计学基础--大数定律、中心极限定理

一、大数定律

统计规律性

• 多次抛掷硬币，正面向上出现的频率接近1/2
• 人口男女比例接近1:1

在随机事件的大量重复出现，往往呈现几乎必然的规律，这类规律就是大数定律

1.1 切比雪夫不等式

1.2弱大数定律

弱大数定律的意义：

1.2伯努利大数定律

伯努利大数定律的意义：

• 伯努利大数定律的结论虽然简单,但其意义却是相当深刻的.它告诉我们当试验次数趋于无穷时,事件A发生的频率依概率收敛于A发生的概率,这样,频率接近于概率这一直观的经验就有了严格的数学意义
• 在实际应用中，当试验次数很大时，便可以用事件的频率来代替事件的概率。例如：

某个箱子里装有若干个白球和红球，具体比例不知道。若从中做1000次有放回抽样，抽出红球100个，白球900个，则我们可以说抽出红球的概率是100/1000=0.1

 

二、中心极限定理

2.1 独立同分布的中心极限定理（独立同分布近似正态分布）

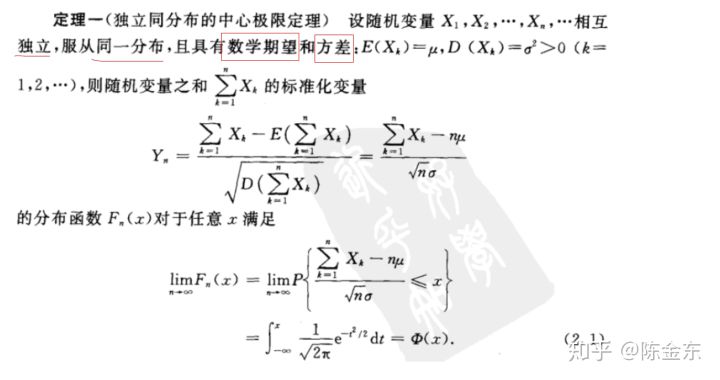
定理说明：n 个相互独立同分布的随机变量之和的分布近似于正态分布，n 愈大，此种近似度愈好

2.2 Lyapunov定理（任何分布近似正态分布）

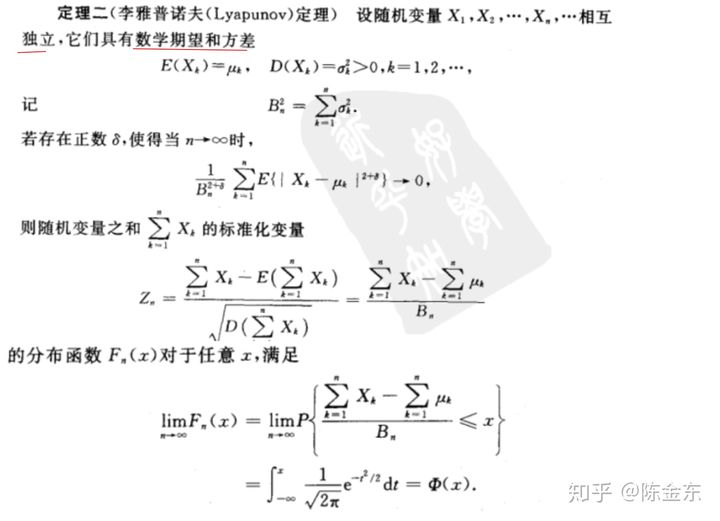
定理说明：

实际应用举例：

如，在任一指定时刻，一个城市的耗电量是大量用户耗电量的总和，从而可以知道这

个城市的耗电量服从正态分布。

 

2.3 Laplace 定理（二项分布近似正态分布）

三、总结

3.1 大数定律小结

大数定律说明了：只要统计的数据量足够多，事物出现的频率就无限接近于其期望值

3.2 中心极限定理小结

3.2.1中心极限定理说明了什么？

• 任何一个样本的平均值将会约等于其所在总体的平均值
• 无论总体是什么分布，任意一个总体的样本平均值都会在总体的平均值周围，呈现正态分布

3.2.2 中心极限定理有什么用？

• 在无法得到总体全部数据的情况下，可以使用样本来估计总体

例如：我们掌握了某个正确抽取样本的平均值和标准差，就能对估计出总体的平均值和标准差。

• 根据总体的平均值和标准差，判断某个样本是否属于总体

例如：我们掌握了某个总体的具体信息，以及某个样本的数据，就能推理出该样本是否就是该群体的样本之一。通过中心极限定理的正态分布，我们就能计算出某个样本属于总体的概率是多少。如果概率非常低，那么我们就能自信满满地说该样本不属于该群体。这也是统计概率中假设检验的原理。