在图论中,拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列。且该序列必须满足下面两个条件:
- 每个顶点出现且只出现一次。
- 若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
有向无环图(DAG)才有拓扑排序,非DAG图没有拓扑排序一说。
拓扑排序常用的两个方法
1、减治技术
- 从 DAG 图中选择一个 没有前驱(即入度为0)的顶点并输出。
- 从图中删除该顶点和所有以它为起点的有向边。
- 重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。
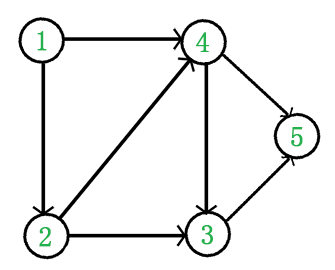
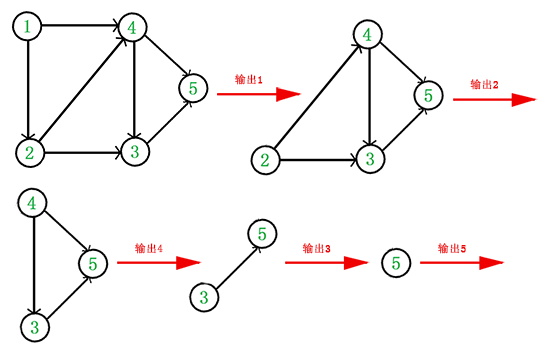
所以拓扑排序结果是1、2、4、3、5
通常,一个有向无环图可以有一个或多个拓扑排序序列。
2、基于DFS来实现
执行一次DFS遍历,并记住顶点变成死端(即退出遍历栈)的顺序,将该次序反过来就得到拓扑排序的一个解。当然在遍历时,不能遇到回边,如果遇到一条回边,该图就不是一个有向无环图,并且对它的顶点进行拓扑排序是不可能的。
当一个顶点v退出DFS栈时,在比v更早出栈的顶点中,不可能存在一个顶点u拥有一条边从u指向v,否则就构成了一个回边。所以在退栈次序的队列中,任何这样的顶点都会排在v的后面,并且在逆序中排在v的前面。

算法:
(1)减治思想的程序,维护一个类Graph,类中定义邻接表list,入度为0的集合,以及每个顶点的入度。
#include<iostream> #include <list> #include <vector> #include <queue> using namespace std; vector<vector<int> >sum; vector<int> temp; /************************类声明************************/ class Graph { int V; // 顶点个数 list<int> *adj; // 邻接表,图的表示方式 queue<int> q; // 维护一个入度为0的顶点的集合 int* indegree; // 记录每个顶点的入度 public: Graph(int V); // 构造函数 ~Graph(); // 析构函数 void addEdge(int v, int w); // 添加边 bool topological_sort(); // 拓扑排序 bool dfs(int u); }; /************************类定义************************/ Graph::Graph(int V) { this->V = V; adj = new list<int>[V]; indegree = new int[V]; // 入度全部初始化为0 for(int i=0; i<V; ++i) indegree[i] = 0; } Graph::~Graph() { delete [] adj; delete [] indegree; } vector<int> c; void Graph::addEdge(int v, int w) { adj[v].push_back(w); ++indegree[w]; } bool Graph::topological_sort() { for(int i=0; i<V; ++i) if(indegree[i] == 0) q.push(i); // 将所有入度为0的顶点入队 int count = 0; // 计数,记录当前已经输出的顶点数 while(!q.empty()) { int v = q.front(); // 从队列中取出一个顶点 q.pop(); cout << v << " "; // 输出该顶点 ++count; // 将所有v指向的顶点的入度减1,并将入度减为0的顶点入栈 list<int>::iterator beg = adj[v].begin(); for( ; beg!=adj[v].end(); ++beg) if(!(--indegree[*beg])) q.push(*beg); // 若入度为0,则入栈 } if(count < V) return false; // 没有输出全部顶点,有向图中有回路 else return true; // 拓扑排序成功 } int main() { Graph g(6); // 创建图 g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); g.topological_sort(); return 0; }
(2)基于DFS的算法
#include<iostream> #include <list> #include <vector> #include <queue> using namespace std; vector<vector<int> >sum; vector<int> temp; /************************类声明************************/ class Graph { int V; // 顶点个数 list<int> *adj; // 邻接表 queue<int> q; // 维护一个入度为0的顶点的集合 int* indegree; // 记录每个顶点的入度 public: Graph(int V); // 构造函数 ~Graph(); // 析构函数 void addEdge(int v, int w); // 添加边 bool topological_sort(); // 拓扑排序 bool dfs(int u); void print(); }; /************************类定义************************/ Graph::Graph(int V) { this->V = V; adj = new list<int>[V]; indegree = new int[V]; // 入度全部初始化为0 for(int i=0; i<V; ++i) indegree[i] = 0; } Graph::~Graph() { delete [] adj; delete [] indegree; } vector<int> c;//用来标记是否被访问 void Graph::addEdge(int v, int w) { adj[v].push_back(w); ++indegree[w]; } vector<int>TopNum;//用来存放最后的拓扑排序结果,最先返回的在最后 int t; bool Graph::dfs(int u)//从一个节点开始,找出dfs序列,返回该节点之后是否存在一个拓扑序列,只要之后遍历到的点和之前的点u有关系(v->u),那么就说明成环!返回false。 { c[u]=-1;//-1表示已经访问过,0表示未访问过 list<int>::iterator beg = adj[u].begin(); for( ; beg!=adj[u].end(); ++beg) { if(c[*beg]==-1) {//大水冲了龙王庙,这个i点在之前已经被遍历到了,成环! return false; } if(!c[*beg]&&!dfs(*beg)) return false; } //经过了检验 c[u]=1;//对应的c不能是-1,也不能是0 TopNum[--t]=u;//逆序存放 return true; } bool Graph::topological_sort() { int h=V; t=V; for(int i=0;i<h;i++) { c.push_back(0); TopNum.push_back(0); } for(int i=0;i<h;i++) if(!c[i]) if(!dfs(i)) return false; return true; } void Graph::print()//输出邻接表,为了检验是否完成图的构造 { for(int i=0;i<V;i++) { list<int>::iterator beg = adj[i].begin(); for( ; beg!=adj[i].end(); ++beg) { cout<<*beg<<'\0'; } } } int main() { Graph g(6); // 创建图 g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); //g.print(); cout<<g.topological_sort()<<endl; for(int i=0;i<TopNum.size();i++) { cout<<TopNum[i]<<'\0'; } return 0; }
另外一种dfs代码
#include<iostream> #include <list> #include <stack> using namespace std; class Graph { int V; // 顶点数 list<int> *adj;//指向邻接表 void topologicalSortUtil(int v, bool visited[], stack<int> &Stack); public: Graph(int V); // 构造函数 // 加入边 void addEdge(int v, int w); // 输出拓扑排序的一个序列 void topologicalSort(); }; Graph::Graph(int V) { this->V = V; adj = new list<int>[V]; } void Graph::addEdge(int v, int w) { adj[v].push_back(w); // Add w to v’s list. } // A recursive function used by topologicalSort void Graph::topologicalSortUtil(int v, bool visited[], stack<int> &Stack) { // 用来标记节点是否被访问 visited[v] = true; // Recur for all the vertices adjacent to this vertex list<int>::iterator i; for (i = adj[v].begin(); i != adj[v].end(); ++i) if (!visited[*i])//如果该节点没有被访问,则调用dfs函数 topologicalSortUtil(*i, visited, Stack); // 把当前节点打入栈中 Stack.push(v); } // 拓扑排序函数,用到了topologicalSortUtil函数 void Graph::topologicalSort() { stack<int> Stack; bool *visited = new bool[V]; for (int i = 0; i < V; i++) visited[i] = false;//初始化为false,表示未被访问过 // 挨个遍历节点,对每个节点进行dfs遍历 for (int i = 0; i < V; i++) if (visited[i] == false) topologicalSortUtil(i, visited, Stack); // Print contents of stack while (Stack.empty() == false) { cout << Stack.top() << " "; Stack.pop(); } } int main() { // Create a graph given in the above diagram Graph g(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); cout << "Following is a Topological Sort of the given graph \n"; g.topologicalSort(); return 0; }
那如果要输出全部的路径呢,比如我需要知道图中所有可行的路径,上图中就是[5,2,3,1],[5,0],[4,0],[4,1]
我选择用dfs的方式,来输出全部的路径。就是找到入度为0的节点,因为所有的路径一定都是从这些节点出发的,然后依次找这些节点的深度优先遍历(在这些节点的邻接表中找),每遍历到一个节点,都将它打入一个vector中,再遍历该节点邻接的一个节点,直到没有后续的路之后(当前节点邻接表为空),将vector放入sum中,每次从入度为0的一个节点开始时,都将temp清零一下,因为这是全新的一个路径。如果到了一个顶点的邻接表尽头,意味着没有再和它相连的点了,那么temp要把该节点pop出来,以便存放另外一个路径。最后,sum的大小就是路径的个数,sum中的序列就是所有的路径。
#include<iostream> #include <list> #include <vector> #include <stack> using namespace std; class Graph { int V; list<int> *adj; bool topologicalSortUtil(int v, bool visited[], stack<int> &Stack); int* indegree; // 记录每个顶点的入度 public: Graph(int V); void addEdge(int v, int w); void topologicalSort(); void printall(); }; vector<vector<int> > sum; vector<int> temp; Graph::Graph(int V) { this->V = V; adj = new list<int>[V]; indegree = new int[V]; // 入度全部初始化为0 for(int i=0; i<V; ++i) indegree[i] = 0; } void Graph::addEdge(int v, int w) { adj[v].push_back(w); ++indegree[w]; } void Graph::printall() { stack<int> Stack; bool *visited = new bool[V]; for (int i = 0; i < V; i++) visited[i] = false; for(int i=0;i<V;i++) { if(indegree[i]==0 && visited[i] == false) { if(topologicalSortUtil(i, visited, Stack)) { temp.clear(); continue; } return; } } } bool Graph::topologicalSortUtil(int v, bool visited[], stack<int> &Stack) { visited[v] = true; temp.push_back(v); // Recur for all the vertices adjacent to this vertex list<int>::iterator i; for (i = adj[v].begin(); i != adj[v].end(); ) { if (!visited[*i]) topologicalSortUtil(*i, visited, Stack); if(++i==adj[v].end()) { temp.pop_back(); } } if(adj[v].empty()) { sum.push_back(temp); temp.pop_back(); } visited[v]=false; // Push current vertex to stack which stores result Stack.push(v); return true; } int main() { // Create a graph given in the above diagram Graph g(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); g.addEdge(5,4); //Graph g(5); // g.addEdge(1,4); // g.addEdge(0,1); // g.addEdge(0,2); // g.addEdge(3,4); g.printall(); cout<<sum.size()<<endl; for(int i=0;i<sum.size();i++) { for(int j=0;j<sum[i].size();j++) { cout<<sum[i][j]<<'\0'; } cout<<endl; } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号