从正整数 N 开始，我们按任何顺序（包括原始顺序）将数字重新排序，注意其前导数字不能为零。
如果我们可以通过上述方式得到 2 的幂，返回 true；否则，返回 false。
示例 1：
输入：1 输出：true
示例 2：
输入：10 输出：false
示例 3：
输入：16 输出：true
示例 4：
输入：24 输出：false
思路：这个题的重点是求出数字的全排列（以0开头的除外），和数字是否2的幂
首先我们来总结下关于全排列。
这是一个c++函数，包含在头文件<algorithm>里面，下面是一般用法的基本格式。
1 int a[]; 2 do{ 3 4 }while(next_permutation(a,a+n));
STL提供了两个用来计算排列组合关系的函数，分别是next_permutation和prev_permutation。首先我们必须了解什么是“下一个”排列组合，什么是“前一个”排列组合。考虑三个字符所组成的序列{a,b,c}。这个序列有六个可能的排列组合：abc，acb，bac，bca，cab，cba。这些排列组合根据less-than操作符做字典顺序(lexicographical)的排序。也就是说，abc名列第一，因为每一个元素都小于其后的元素。acb是次一个排列组合，因为它是固定了a(序列内最小元素)之后所做的新组合。同样道理，那些固定b(序列中次小元素)而做的排列组合，在次序上将先于那些固定c而做的排列组合。以bac和bca为例，bac在bca之前，因为次序ac小于序列ca。面对bca，我们可以说其前一个排列组合是bac，而其后一个排列组合是cab。序列abc没有“前一个”排列组合，cba没有“后一个”排列组合。
所以一般在用next_permutation函数之前，都将数字排序好，按照从小到大的顺序。
下面来分析下next_permutation函数具体是怎么实现的。
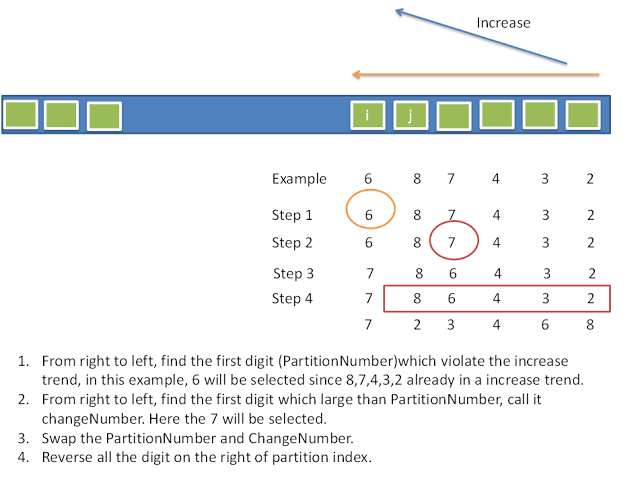
- 从右往左扫描,发现第一个左邻小于右邻的数字,称之为 PartitionNumber, 如上图,
6恰好是我们找到的 PartitionNumber . - 依然从右到左进行扫描,发现第一个比 PartitionNumber 要大的数,称之为 ChangeNumber.而7恰好是我们找到的 ChangeNumber ,需要注意的是,这样的数一定是存在的,否则的话,就找不到所以的 PartitionNumber 了.
- 交换 PartitionNumber 和 ChangeNumber.这样一步,会使得新的排列组成的数比旧的排列组成的数要大,当然,新数增长的幅度不一定是最小的.
- 交换之后，将当前ChangeNumber后面的数（或者原来PartitionNumber位置之后的数）从小到大排列一下,如此反转之后,可以保证,新的排列组成的数的增长幅度在所有的可能中最小.
template<calss BidrectionalIterator> bool next_permutation(BidrectionalIterator first,BidrectionalIterator last) { if(first == last) return false; /* 空区间 */ BidrectionalIterator i = first; ++i; if(i == last) return false; /* 只有一个元素 */ i = last; /* i指向尾端 */ --i; for(;;) { BidrectionalIterator ii = i; --i; /* 以上锁定一组(两个)相邻元素 */ if(*i < *ii) /* 如果前一个元素小于后一个元素 */ { BidrectionalIterator j = last; /* 令j指向尾端 */ while(!(*i < *--j)); /* 由尾端往前找，直到遇到比*i大的元素 */ iter_swap(i,j); /* 交换i,j */ reverse(ii,last); /* 将ii之后的元素全部逆序重排 */ return true; } if(i == first) /* 进行至最前面了 */ { reverse(first,last); /* 全部逆序重排 */ return false; } } }
接着我们讨论下，如何判断一个数是2的幂。
我们知道，1个数乘以2就是将该数左移1位，而2的0次幂为1， 所以2的n次幂（就是2的0次幂n次乘以2）就是将1左移n位， 这样我们知道如果一个数n是2的幂，则其只有首位为1，其后若干个0，必然有n & (n - 1)为0。（在求1个数的二进制表示中1的个数的时候说过，n&(n-1)去掉n的最后一个1）。因此，判断一个数n是否为2的幂，只需要判断n&(n-1)是否为0即可。
那如何判断是2的多少次方呢
int log2(int value) //递归判断一个数是2的多少次方 { if (value == 1) return 0; else return 1+log2(value>>1); }
下面附上本题的完整代码
bool reorderedPowerOf2(int n) { int i,j,k,tmp; vector<int> a; a.clear(); while (n>0) { a.push_back(n%10); n/=10; } sort(a.begin(),a.end()); do { if (a[0]==0) continue; tmp=0; for (i=0;i<a.size();i++) tmp=tmp*10+a[i]; if((tmp&tmp-1)==0)return true; }while (next_permutation(a.begin(),a.end())); return false; }
