Data Compression
数据压缩
introduction
压缩数据可以节省存储数据需要的空间和传输数据需要的时间,虽然摩尔定律说集成芯片上的晶体管每 18-24 个月翻一倍,帕金森定律说数据会自己拓展来填满可用空间,但数据压缩还是最经济的做法。
数据压缩的基本模型如下,很简单,压缩和解压,压缩率即 C(B) 和 B 的比特数之比。

数据压缩的对象本质上是二进制文件,抽象层次是比特流,所以有必要贴下课程里怎么读写二进制文件。

大多数系统的输入输出系统,像 Java,是基于 8 位的字节流,上面输入的数据可以不用和字节边界对齐。

输出的 colse() 方法会在比特流的最后一个字节用 0 补齐,以保证和文件系统的兼容性。
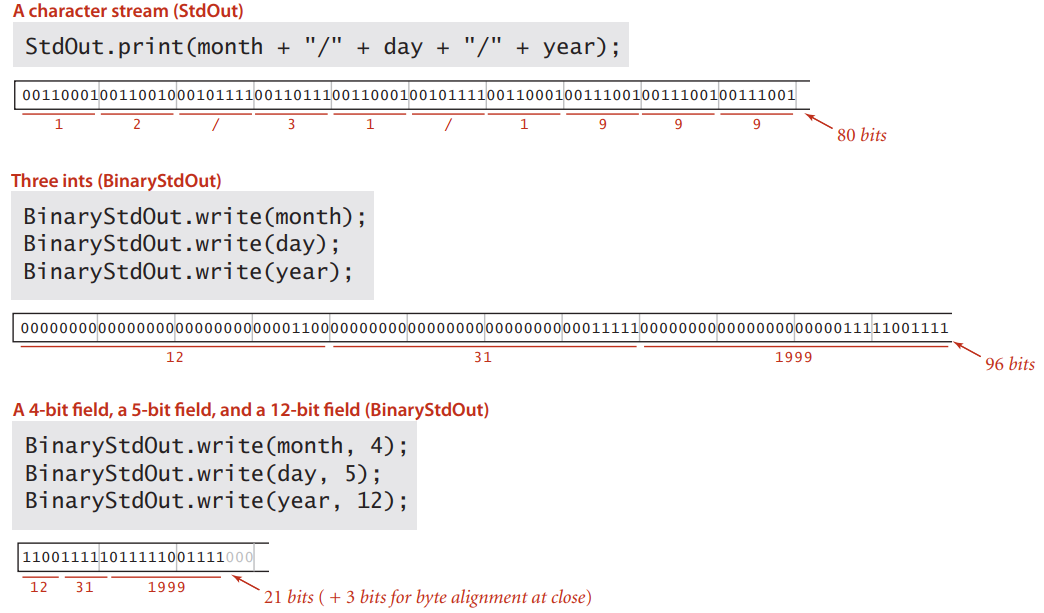
这是一个数据压缩的简单例子,用三种不同方式来表示日期 12/31/1990。第一种把日期当做字符串,每位用一个字节的字符类型表示,需要 80 位。第二种用三个 int 类型,需要 96 位。第三种的编码是变长的,像月份只要 4 位就能编码,而且最后补了 3 个 0 来兼容字节流,总计 24 位。这是最粗糙的数据压缩方式。
转储(dump)表示的是比特流的一种可供人类阅读的形式,用于帮助我们在调试的时候检查比特流或者字节流的内容。下图是一些例子:BinaryDump 将比特流按 0 和 1 输出来;HexDump 将比特流组织成 8 位并用两位的 16 进制数表示;PictureDump 则将比特流变为 Picture 对象,其中白色像素表示 0,黑色像素表示 1。

最后我们需要认识到一点:通用数据压缩算法是不存在的。这其实也很好理解,要是存在这样的算法,那意味着我们可以再对压缩文件进行压缩,循环往复到文件大小为零,显然是不合理的。
run-length Coding
比特流中最简单的冗余就是一长串重复的比特,游程编码(run-length coding)就利用这冗余来压缩数据。例子:

原理也很简单,就是统计重复的个数,直接记总数而不是全部写出来。上图的例子中用了 4 位计数,下面的代码里用了 8 位,最多能计到 255。要是有 300 个 1,计满 255 后再插入 8 位 0,表示有 0 个 0,然后再继续计剩下的 45 位就好。代码:
public class RunLength {
private final static int R = 256; // maximum run-length conut
private final static int lgR = 8; // number of bits per conut
public static void compress() {
char cnt = 0;
boolean b, old = false;
while (!BinaryStdIn.isEmpty()) {
b = BinaryStdIn.readBoolean();
if (b != old) {
BinaryStdOut.write(cnt);
cnt = 0;
old = !old;
} else {
if (cnt == 255) {
BinaryStdOut.write(cnt);
cnt = 0;
BinaryStdOut.write(cnt);
}
}
cnt++;
}
BinaryStdOut.write(cnt);
BinaryStdOut.close();
}
public static void expand() {
boolean bit = false;
while (!BinaryStdIn.isEmpty()) {
int run = BinaryStdIn.readInt(lgR); // read 8-bit conut from standard input
for (int i = 0; i < run; i++)
BinaryStdOut.write(bit); // write 1 bit to standard output
bit = !bit;
}
BinaryStdOut.close(); // pad 0s for byte alignment
}
}
这种策略对实际应用中经常出现的几种比特流十分有效,游程编码的一个应用是压缩位图(bitmap),位图被广泛用于保存图片和扫描文档。简单起见,我们将二进制位图数据组织为将像素按行排列的比特流。可以看到,右边压缩后的比特流显然小了很多。

游程编码不适用于含有大量短游程的输入,而不是所有我们希望压缩的比特流都含有较长的游程,所以下面来介绍两种适用于多种类型的文件压缩算法。
Huffman Compression
哈夫曼压缩和第一个年月日的例子一样,都采取变长编码,哈夫曼的原理就是用较短的编码来表示频率较高的字符,从而达到节省空间的目的。而变长编码存在多义性(ambiguity)的问题,用摩斯密码举例说明:
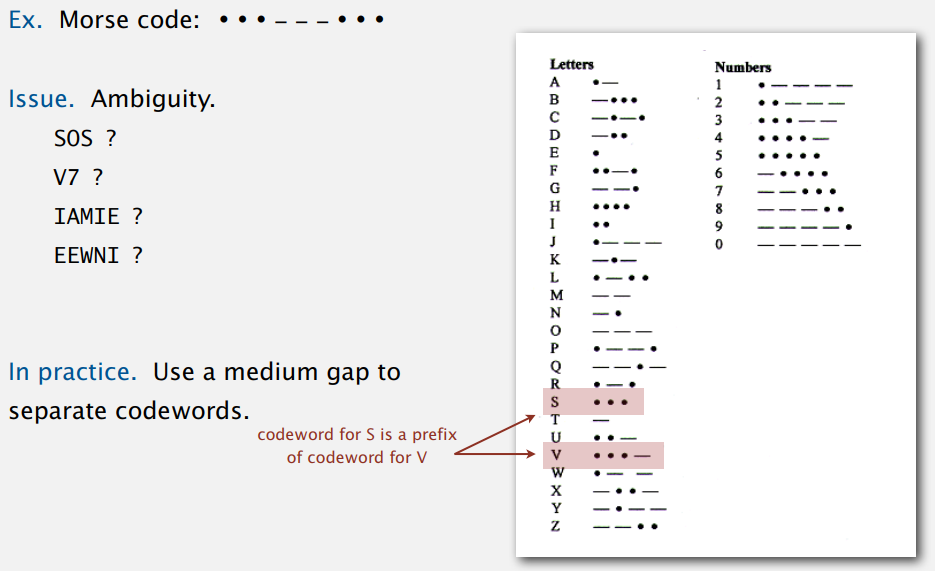
...---... 是最常用的摩斯密码,表示 SOS,但是从上表来看,也可以解读为 V7、IAMIE 和 EEWNI,所以实际上密码之间还有一定的间隙隔开,以避免错误的解读。
多义性的本质原因是有些字符的编码是其它字符编码的前缀,所以才可能会有不同的解读。而有种特殊的变长编码——前缀码(prefix-free code),字符编码肯定不是其它字符编码的前缀,也就不存在多义性的问题。
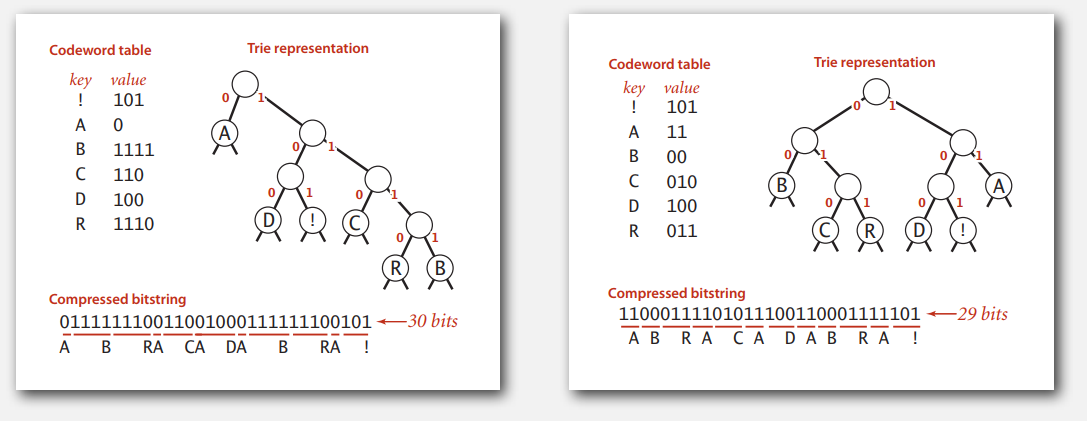
前缀码可以很自然地用 Trie 来表示,被编码的字符都在叶子结点上,也就没有谁是谁的前缀。同时,也可以发现前缀码不是唯一的,那也就存在一个最优的前缀码,使得压缩后的比特流最短。
Trie Node
private static class Node implements Comparable<Node> {
private final char ch; // used only for leaf nodes
private final int freq; // used only for compress
private final Node left, right;
public Node(char ch, int freq, Node left, Node right) {
this.ch = ch;
this.freq = freq;
this.left = left;
this.right = right;
}
private boolean isLeaf() {
return left == null && right == null;
}
public int compareTo(Node that) {
return this.freq - that.freq;
}
}
字符出现频率在下面生成最优前缀码的时候会用到。
用 Trie 表示的前缀码对文件进行压缩后,还要把 Tire 附上,解压(展开,expand)时才知道怎么做。所以得把 Trie 写入比特流,解压时再从比特流中读出来,这边按前序遍历的顺序来读写。

到叶子结点都会先输出个 true(比特 1),内部结点则是 0,为读做了记号的感觉。当压缩文件很大时,附在开头的 Trie 相对就会显得很小,没有什么关系。

在比特流中碰到 1,说明接下来 8 比特是叶子结点的字符,于是读入 8 位。
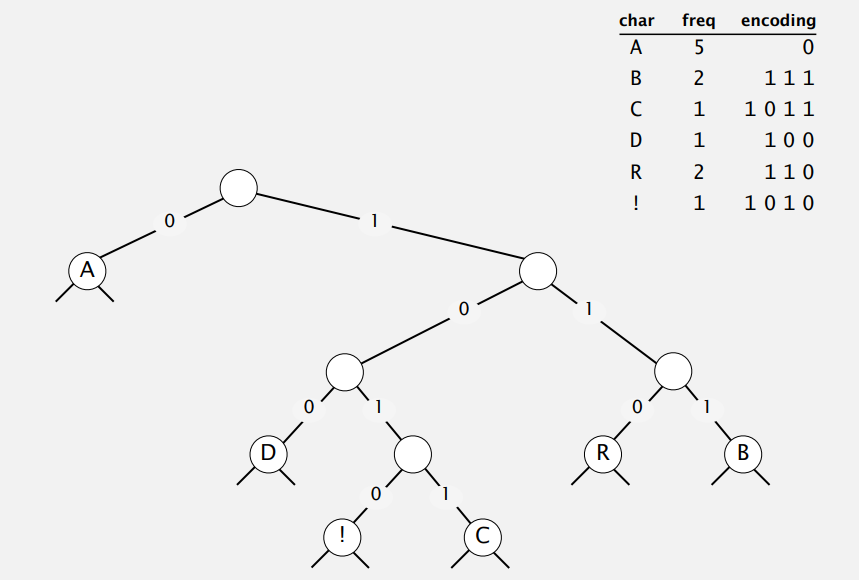
现在,我们大概知道了要用 Trie 来压缩,以及怎么传输 Trie 好用于解压,关键的如何构造 Trie 还没说,特别得是构造最优前缀码的 Trie。实际上,哈夫曼的做法很好描述:首先你要知道字符出现的频率,然后每次挑两个最小的加起来,加起来的值再和原来的那些一起重复挑两个最小的加起来,从下往上接成 Trie。
Constructing Huffman Trie
private static Node buildTrie(int[] freq) {
MinPQ<Node> pq = new MinPQ<Node>();
for (char i = 0; i < R; i++)
if (freq[i] > 0)
pq.insert(New Node(i, freq[i], null, null));
// merge two smallest tries
while (pq.size() > 1) {
Node x = pq.delMin();
Node y = pq.delMin();
Node parent = new Node('\0', x.freq + y.freq, x, y);
pq.insert(parent);
}
return pa.delMin();
}
Optimal
首先,需要个标准来判断各前缀码优劣。有个概念叫 Trie 的 加权外部路径长度,等于所有叶子结点的频率和其深度的乘积总和,也就是压缩后字符集的长度。最优前缀码 Trie T 的加权外部路径长度最小,记为 \(B(T)\)。
证明: 对规模为 n (不小于 2)的字符集(至少两个不同字符),哈夫曼算法可以构造出一个最优的前缀码 Trie。
-
当 n = 2 时,两个字符只能分别用 0 和 1 表示,显然成立。
-
假设哈夫曼算法对规模为 K(大于 2)的字符集能构造出一个最优前缀码 Trie。
-
现在考虑规模为 K + 1 的字符集 \(C = \{x_{1}, x_{2},...,x_{k + 1}\}\),其中 \(x_{1}, x_{2} \in C\) 是频率最小的两个字符。
令 \(C^{'} = (C - \{x_{1}, x_{2}\}) \cup \{z\}\),其中 \(f_{z} = f_{x_{1}} + f_{x_{2}}\)(\(f_{x}\) 为字符 x 出现的频率)。
根据假设,哈夫曼算法可以构造出规模为 K 的字符集 \(C^{'}\) 的一个最优前缀码 Trie,不妨记做 \(T^{'}\)。对 \(T^{'}\) 中表示 \(z\) 的叶子结点添加两个孩子 \(x_{1}\) 和 \(x_{2}\) 得到的新 Trie 记做 \(T\)(相当于直接对 \(C\) 用哈夫曼构造出来的)。
用反证法证明 \(T\) 就是字符集 \(C\) 的一个最优前缀码 Trie,为此需要先了解下面两个引理。
-
\(B(T^{'}) = B(T) - (d + 1)(f_{x_{1}} + f_{x_{2}}) + d(f_{x_{1}} + f_{x_{2}}) = B(T) - (f_{x_{1}} + f_{x_{2}})\)(d 为深度)。
-
存在 \(C\) 的一个最优前缀码 Trie,\(x_{1}\) 和 \(x_{2}\) 是最深叶子且为兄弟。这个不难证明,稍作计算就可以发现把 \({x_{1}}, x_{2}\) 和最深兄弟叶子结点交换不会增加加权外部路径长度。所以只要有一个最优,就能交换成上面的形式,也就肯定存在。
假设字符集 \(C\) 存在着更优的 \(T^{*}\),即有 \(B(T^{*}) < B(T)\)。且根据引理二,不妨认为 \(T^{*}\) 即为 \({x_{1}}, x_{2}\) 是最深兄弟叶子结点的形式。从这样的 \(T^{*}\) 里,类似地去掉 \({x_{1}}, x_{2}\) 得到 \(T^{*'}\)。由引理一有:
\(B(T^{*'}) = B(T^{*}) - (f_{x_{1}} + f_{x_{2}}) < B(T) - (f_{x_{1}} + f_{x_{2}}) = B(T^{'})\)
和 \(T^{'}\) 是字符集 \(C^{'}\) 的最优前缀码 Trie 矛盾,故 \(T\) 是字符集 \(C\) 的最优前缀码 Trie。
所以哈夫曼构造了规模为 K + 1 的字符集 C 的最优前缀码 Trie T,归纳得证。
-
参考链接:点我。
LZW-compression
LZW 压缩算法是自适应性的(adaptive)模型,在读入文本的时候学习并更新模型,不需要将模型附在比特流中用于解压,但解压的时候只能从文本开头开始。
算法原理并不复杂,直接来看压缩和展开的例子。
Compression Example
压缩可以概括成这几个步骤:
- 创建符号表,键为字符串,值为字符串对应的定长编码。
- 初始化符号表,加入单个字符的键值对。
- 在符号表键中找文本未扫描部分的最长前缀 s,输出 s 对应的值(编码)。
- 预读文本下一个字符 c,更新符号表,新键为字符串 s + c。
- 重复上两步直到文本结束。
例图中编码长度为 8 位,用两位 16 进制表示,单字符编码即 7 位标准 ASCII 中的值,像 A 是 41(0100 0001)。编码 80 保留为表示文本结束,新键 s + c 的编码从 81 开始。
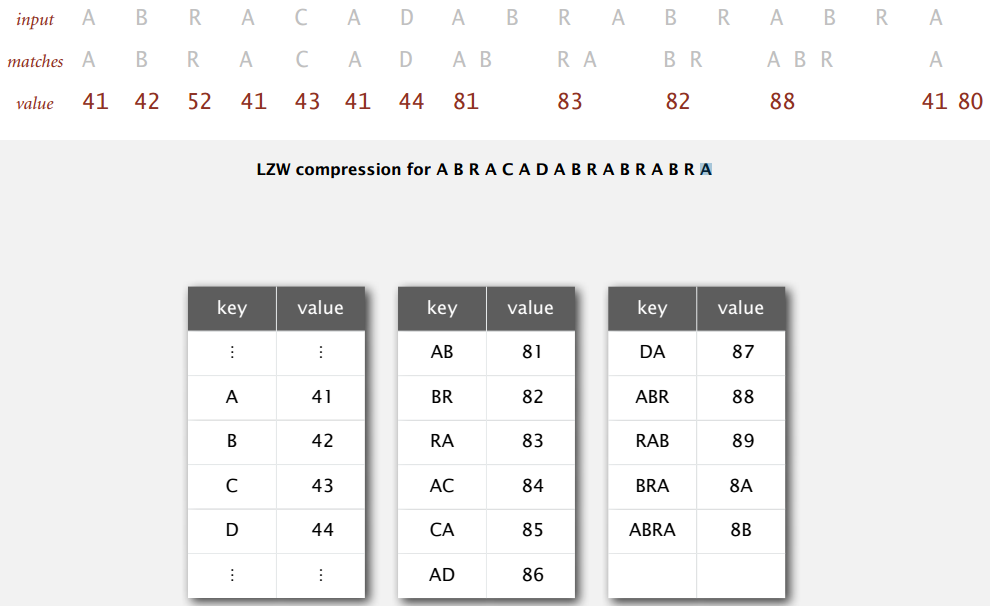
文本未扫描部分在符号表键中最长前缀,一开始是 A,于是编码成 41,接着预读下一位 B,往符号表中加入新键值对 (AB, 81);下一个最长前缀是 B,编码 42,预读并加入新键值对 (BR, 82);... 读完 D 之后,最长前缀为 AB,编码 81,预读并加入新键值对 (ABR, 88);... 文本结束编码为 80。
最长前缀用 Trie 来获取,代码用了 TST:
public static void compress() {
// R 表示字符总数,例图是 0x80
// L 表示编码最大值,例图是 0xFF
// W 表示编码宽度,例图是 8 位
String input = BinaryStdIn.readString();
TST<Integer> st = new TST<Integer>();
for (int i = 0; i < R; i++)
st.put("" + (char) i, i);
int code = R + 1; // 新键编码从 0x81 开始
while (input.lenght() > 0) {
String s = st.longestPrefixOf(input);
BinaryStdOut.write(st.get(s), W);
int t = s.length();
if (t < input.length() && code < L)
st.put(input.substring(0, t + 1), code++); // 更新符号表
input = input.substring(t);
}
BinaryStdOut.write(R, W); // 写上 0x80 表示文件结束
BinaryStdOut.close();
}
LZW 算法就是这样用定长的编码来表示越来越长的字符串来节省空间的,当编码都用完了,在例子中就是有字符串被编码为 FF 时,就全部丢掉重新开始,或是当不再有效时丢掉,这里不展开讨论。
Expand Example
展开和压缩类似,有下面几个步骤:
- 创建符号表,但这次编码为键,对应的字符串为值。
- 初始化符号表,加入单个字符的键值对。
- 从压缩文件读入 W 位的编码,输出编码对应的字符串。
- 预读下一个编码,得到下个字符,类似地更新符号表。
- 重复上两步直到读入结束编码。
例图即展开上面压缩形成的编码。
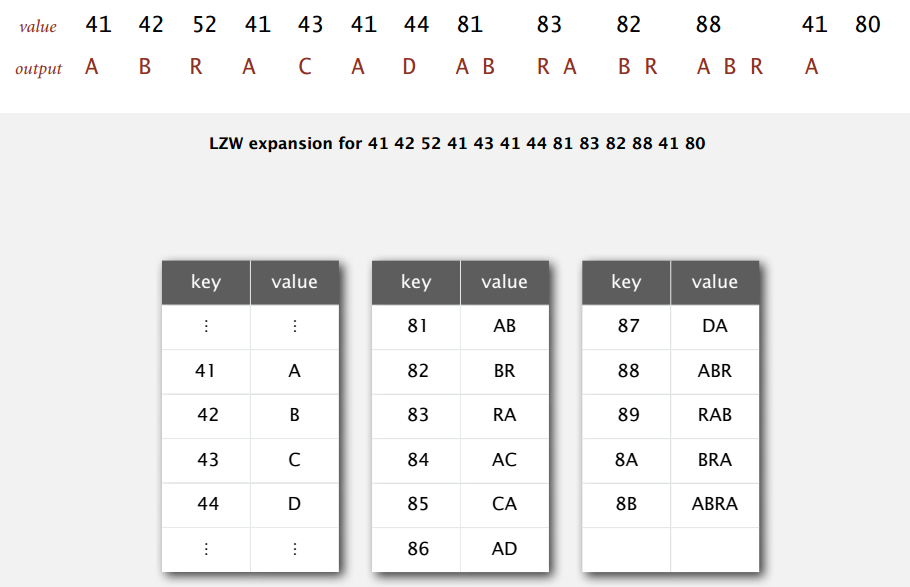
一开始读入 8 位编码 41,从符号表可知对应字符串 A,输出 A 后预读下一个编码 42,对应 B,于是往符号表中加入新键值对 (81, AB);现在读到编码 42,输出 B 并预读 52 得到 R,所以加入 (82, BR) ... 直到读入编码 80,表示文件结束。
似乎展开和压缩差不多,甚至更简单,因为不需要找最长前缀,符号表直接用数组简单实现。但是,展开有时会碰到一个特殊的情况:

压缩字符串 ABABABA 编码成 41 42 81 83 80,现在对这编码进行展开。编码 41 输出 A,预读 42 后加入 (81, AB) 更新符号表;编码 42 输出 B,预读 81 知道下个字符是 A,加入 (82, BA);编码 81 输出 AB,预读 83 卡住,因为符号表中还没有这个键。
但是,这种时候我们还是可以知道 AB 的下一个字符是什么的。假设 AB 后面的字符分别为 \(c_{1}\),\(c_{2}\),\(c_{3}\),卡住的时候(更新要加入的编码和预读到的编码一样)肯定有 AB\(c_{1}\) = \(c_{1}c_{2}c_{3}\),所以下个字符即 A,加入 (83, ABA) 即可。
代码:
public static void expand() {
int i; // 当前更新符号表要加入的编码
String[] st = new String[L];
for (i = 0; i < R; i++)
st[i] = "" + (char) i;
st[i++] = " "; // 例图中表示文件结束的 0x80
int codeword = BinaryStdIn.readInt(W);
String val = st[codeword];
while (true) {
BinaryStdOut.write(val);
codeword = BinaryStdIn.readInt(W); // 预读的编码
if (codeword == R) break;
String s = st[codeword];
if (i == codeword) // 要加入的编码和预读的编码相同
s = val + val.charAt(0);
if (i < L)
st[i++] = val + s.charAt(0);
val = s;
}
BinaryStdOut.close();
}
可以看到不用传输模型就能展开压缩的编码文件。


